Function and its aniderivative

Problem

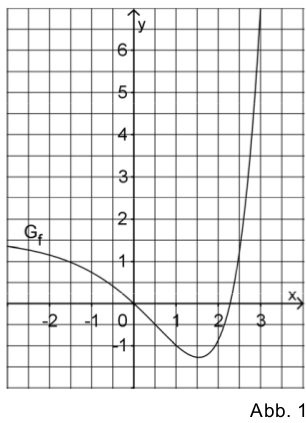
Figure 1 displays the graph \(G_f\) of a function \(f\) defined in \(\mathbb{R}\). Sketch in figure 1 the graph of the integral function \(F:x\mapsto \int\limits_1^x f(t)\mathrm{d}t\) defined in \(\mathbb{R}\). Consider with appropriate precision in particular the zeros and extrema of \(F\) as well as \(F(0)\).

Solution

If a function possesses a zero with a change of sign, the corresponding antiderivative possesses a local extremum at this point. It is a maximum if the slope of the function is negative. If, on the other hand, the slope is positive, the antiderivative has a minimum at that point.

Considering the function given in the problem text, one finds zeros of \(f(x)\) at \(x_1=0\) and \(x_2\approx 2.25\). In the first case, the slope is negative so that \(F(0)\) represents a local maximum of the antiderivative. At the other point \(x_2\) the slope of \(f\) is positive so that \(F(x_2)\) is a local minimum.

Another property of \(F(x)\) follows from the lower limit of integration at \(t=1\). As a consequence, \(F(1)=0\). Finally, from counting squares, \(F(0)=-\int\limits_0^1 f(t)\mathrm{d}t\) can be estimated to equal \(\frac{1}{2}\).

By means of Sage, we can carry out the integration provided the function \(f\) is known. We choose

\[f(x)=\frac{49}{5}\frac{x(4x-9)}{(2x-9)^2},\]

which possesses the properties used in the above reasoning. In addition, its qualitative form resembles that given in figure 1.