Integrals of semicircle

Problem

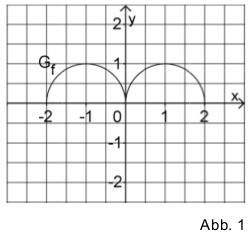
Figure 1 displays the graph \(G_f\) of the function \(f\) with the domain \([-2;2]\). The graph consists of two half-circles with centers at \((-1\vert 0)\) and \((1\vert 0)\), respectively, and a radius of \(1\). Consider the antiderivative \(F: x \mapsto \int\limits_0^x f(t)\mathrm{d}t\) defined in \([-2;2]\).

1. State the values of \(F(0)\), \(F(2)\), and \(F(-2)\).

2. Add a sketch of the graph of \(F\) to figure 1.

Solution of part a

In view of the limits of integration of \(F\) one finds for \(F(0)\):

\[F(0) = \int_0^0 f(t)\mathrm{d}t = 0 .\]

For \(F(2)\) one integrates over the area of a half-circle with radius \(1\). With the area of a circle of radius \(r\) given by \(\pi r^2\), one obtains

\[F(2) = \frac{\pi}{2} .\]

As a consequence of the symmetry of the function \(f(x)\), its antiderivative is antisymmetric:

\[F(-x) = \int_0^{-x} f(t)\mathrm{d}t = -\int_{-x}^0 f(t)\mathrm{d}t = -\int_0^x f(-t)\mathrm{d}t = -\int_0^x f(t)\mathrm{d}t = -F(x)\]

Correspondingly, \(F(-2) = -\frac{\pi}{2}\).

These results may be checked by means of Sage:

Solution of part b

The function being defined piecewise, it is best to carry out the symbolic integration in Sage piecewise as well. Then we are able to display the function \(f\) and its antiderivative.