Tree diagram

Aufgabe

The following tree diagram is related to a random experiment with events \(C\) and \(D\).

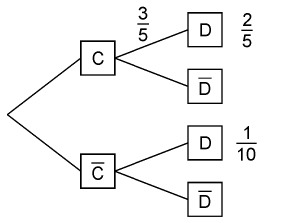
1. Calculate \(P(\bar{D})\).

2. Prove that \(C\) and \(D\) are statistically dependent.

3. Modify the value \(\frac{1}{10}\) in the tree diagram so that \(C\) and \(D\) are statistically independent.

Solution of part a

The probability \(P(D)\) results from the given tree diagram as

\[P(D) = P(C\cap D)+P(\bar{C}\cap D) = \frac{2}{5}+\frac{1}{10} = \frac{1}{2}\]

The condition \(P(D)+P(\bar{D})=1\) leads to \(P(\bar{D})=\frac{1}{2}\).

Solution of part b

Two events \(C\) and \(D\) are statistically dependent if the occurrence of event \(C\) has an influence on the probability of event \(D\), i.e. \(P(D|C)\neq P(D|\bar{C})\). From the tree diagram we read off \(P(D|C)=\frac{3}{5}\).

In addition, we need

\[P(C) = \frac{P(C\cap D)}{P(D|C)} = \frac{2/5}{3/5} = \frac{2}{3},\]

which results in \(P(\bar C) = 1-P(C)=\frac{1}{3}\) and finally in

\[P(D|\bar{C}) = \frac{P(\bar{C}\cap D)}{P(\bar C)}=\frac{1/10}{1/3} = \frac{3}{10}.\]

This proves \(P(D|C)\neq P(D|\bar{C})\) so that \(C\) and \(D\) are indeed statistically dependent.

Solution of part c

In contrast to the previous task, the condition \(P(D|C)=P(D|\bar{C})\) has to hold. \(P(\bar{C})\) is still given as \(\frac{1}{3}\) so that

\[P(\bar{C}\cap D) = P(D|\bar{C})\cdot P(\bar{C}) = P(D|C)\cdot P(\bar{C}) = \frac{3}{5}\cdot\frac{1}{3}=\frac{1}{5}.\]

We will calculate all probabilities of the tree diagram with Sage by using the conditions

\[ \begin{align}\begin{aligned}P(C)+P(\bar{C}) = 1\\P(D|C)+P(\bar{D}|C) = 1\\P(D|\bar{C})+P(\bar{D}|\bar{C}) = 1\\P(D|C)\cdot P(C) = P(C\cap D)\\P(\bar{D}|C)\cdot P(C) = P(C\cap\bar{D})\\P(D|\bar{C})\cdot P(\bar{C}) = P(\bar{C}\cap D)\\P(\bar{D}|\bar{C})\cdot P(\bar{C}) = P(\bar{C}\cap\bar{D}).\end{aligned}\end{align} \]

The values of \(P(D|C)\), \(P(C\cap D)\), and \(P(\bar{C}\cap D)\) can be modified in the list probabilities.