The cuboid

Problem

The vectors

\[\begin{split}\vec{a} = \left(\begin{matrix} 2\\1\\2 \end{matrix} \right),\quad \vec{b} = \left(\begin{matrix} -1\\2\\0 \end{matrix} \right),\quad \vec{c_t} = \left(\begin{matrix} 4t\\2t\\-5t \end{matrix} \right),\end{split}\]

generate a geometric body for every \(t\) with \(t\in\mathbb{R}\backslash\{0\}\). The figure below illustrates this for an example of \(t\).

1. Prove that the generated body is always a cuboid.

2. Determine the values of \(t\) leading to a cuboid with a volume of 15.

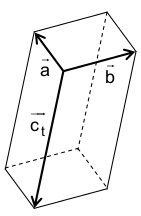
Solution of part a

The generated body is a cuboid if and only if the vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are mutually orthogonal. Therefore, we calculate all possible inner products of two vectors and verify that all of them vanish.

\[\begin{split}\vec{a}\cdot\vec{b} = 2\cdot(-1) + 1\cdot2 + 2\cdot0 = 0\\ \vec{a}\cdot\vec{c} = 2\cdot4t + 1\cdot2t + 2\cdot(-5t) = 0\\ \vec{b}\cdot\vec{c} = (-1)\cdot4t + 2\cdot2t + 0\cdot(-5t) = 0\\\end{split}\]

The fact that every inner product vanishes proves that the generated body is a cuboid for any value of \(t\). The inner products can also be calculated with Sage:

Solution of part b

The volume of a cuboid can be calculated with the scalar triple product:

\[\begin{split}V = \left\vert\vec{a}\cdot(\vec{b}\times\vec{c})\right\vert\\ =\left\vert\left(\begin{matrix} 2\\1\\2 \end{matrix} \right) \cdot\left(\begin{matrix} 2\cdot(-5t)-0\cdot2t \\ 0\cdot4t-(-1)\cdot(-5t) \\ (-1)\cdot2t-2\cdot4t \end{matrix}\right)\right\vert \\ =\left\vert 2\cdot(-10t) + 1\cdot(-5t)+2\cdot(-10t) \right\vert\\ = 45\left\vert t \right\vert.\end{split}\]

Together with the condition that the cuboid’s volume should be equal to 15, we obtain

\[V = 45\left\vert t \right\vert \overset{!}{=} 15\]

which can be rewritten as

\[\left\vert t \right\vert = \frac{1}{3} \Leftrightarrow t=\pm\frac{1}{3}.\]

We obtain two possible solutions for \(t\). In one case, the vector \(c\) points towards the upper half-space while in the other case it points towards the lower half-space.

This result can be verified with the help of Sage. In particular, the evaluation of the triple product is significantly simplified.