Properties of graphs of functions

Problem

Given are the functions \(f, g\) and \(h\) defined on \(\mathbb{R}\) by \(f(x)=x^2-x+1\), \(g(x)=x^3-x+1\), and \(h(x)=x^4+x^2+1\).

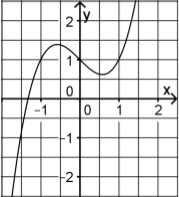
1. The figure depicts the graph of one of the three functions. Indicate which functions is represented by the graph. Argue why the graph cannot represent the other two functions.

2. The first derivative of the function \(h\) is given by \(h'\). Evalute \(\int_0^1h'(x)\mathrm{d}x\).

Solution of part a

The graph displays two extrema. Therefore, it cannot represent the function \(f(x)\) because the derivative of a quadratic function possesses only one zero. Furthermore, the function displayes in the figure takes on negative values, excluding the function \(h(x)\) aus. As a consequence the graph represents the function \(g(x)\). We check our conjecture with the help of Sage:

The graph of the function \(g(x)\) shown in red indeed fits the graph in the original figure.

Solution of part b

The antiderivative of the derivative of a function is the function itself. It follows

\[\int_0^1h'(x)\mathrm{d}x = h(1)-h(0) = 3-1 = 2.\]

In Sage, we start by differentiating the function \(h(x)\) as a check and continue by evaluating the required definite integral:

Of course, according to our reasoning above, we obtain the same result by subtracting the function taken at the limits of integration: