Tree diagrams

Problem

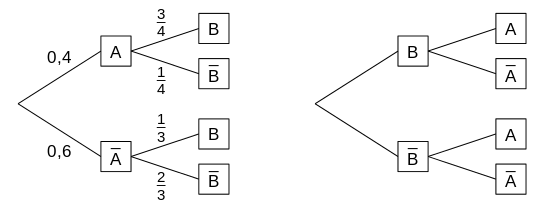
The two tree diagrams belong to the same random experiment with events \(A\) and \(B\).

Compute the probability \(P(B)\) and, subsequently, add the corresponding probabilities to each branch in the right tree diagram.

(Partial result: P(B)=0.5)

Solution

The probability \(P(B)\) results from the information given in the left tree diagram as

\[P(B) = P(B\cap A)+P(B\cap \bar{A}) = P(B|A)\cdot P(A) + P(B|\bar{A})\cdot P(\bar{A}) = \frac{3}{4}\cdot 0.4 + \frac{1}{3}\cdot 0.6 = 0.5\]

Then, the condition \(P(B)+P(\bar{B})=1\) yields \(P(\bar{B})=0.5\). The probabilities corresponding to the remaining branches can be determined by means of Bayes’ theorem.

\[ \begin{align}\begin{aligned}P(A|B) = \frac{P(B|A)\cdot P(A)}{P(B)} = \frac{\frac{3}{4}\cdot 0.4}{0.5} = \frac{3}{5}\\P(\bar{A}|B) = \frac{P(B|\bar{A})\cdot P(\bar{A})}{P(B)} = \frac{\frac{1}{3}\cdot 0.6}{0.5} = \frac{2}{5}\\P(A|\bar{B}) = \frac{P(\bar{B}|A)\cdot P(A)}{P(\bar{B})} = \frac{\frac{1}{4}\cdot 0.4}{0.5} = \frac{1}{5}\\P(\bar{A}|\bar{B}) = \frac{P(\bar{B}|\bar{A})\cdot P(\bar{A})}{P(\bar{B})} = \frac{\frac{2}{3}\cdot 0.6}{0.5} = \frac{4}{5}\end{aligned}\end{align} \]

We can use Sage to determine all probabilities of the right tree diagram on the basis of the given probabilities and the conditions

\[ \begin{align}\begin{aligned}P(B)+P(\bar{B}) = 1\,,\\P(A|B)+P(\bar{A}|B) = 1\,,\\P(A|\bar{B})+P(\bar{A}|\bar{B}) = 1\,,\\P(A|B) \cdot P(B) = P(B|A) \cdot P(A)\,,\\P(A|\bar{B}) \cdot P(\bar{B}) = P(\bar{B}|A) \cdot P(A)\,,\\P(\bar{A}|B) \cdot P(B) = P(B|\bar{A}) \cdot P(\bar{A})\,,\\P(\bar{A}|\bar{B}) \cdot P(\bar{B}) = P(\bar{B}|\bar{A}) \cdot P(\bar{A})\,.\end{aligned}\end{align} \]

The values of the left tree diagram can be set in the list probabilities.