The cube

Problem

Consider the cube \(ABCDEFGH\) depicted in the figure.

The vertices \(D\), \(E\), \(F\) and \(H\) of this cube have the following coordinates in a cartesian coordinate system: \(D(0|0|-2)\), \(E(2|0|0)\), \(F(2|2|0)\) and \(H(0|0|0)\).

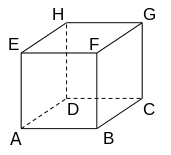
1. Add coordinate axes to the figure and label them accordingly. Give the coordinates of point \(A\).

2. The point \(P\) lies on the edge \([FB]\) of the cube and has a distance of \(3\) from point \(H\). Compute the coordinates of point \(P\).

Solution of part a

The point \(H\) lies in the origin of the coordinate system. Moreover, point \(E\) lies on the positive \(x_1\)-axis and point \(D\) on the negative \(x_3\)-axis. Since the \(x_2\)-coordinate of \(F\) is positive, \(G\) lies on the positive \(x_2\)-axis. The coordinate system can be drawn as shown in the following figure.

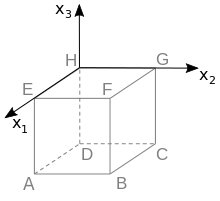
The coordinates of \(A\) thus follow as \((2|0|-2)\).

Based on the vectors from \(H\) to \(D\) and \(E\), respectively, one can obtain this result also with the help of Sage.

Solution of part b

Point \(P\) can be determined as the intersection of the edge \([FB]\) and a sphere centered on \(H\) with radius \(3\). The edge is parametrized by the equation

\[\begin{split}[FB]: \vec{X} = \vec{F} + \lambda \cdot \vec{FB} = \begin{pmatrix} 2\\2\\0 \end{pmatrix}+\lambda\cdot \begin{pmatrix}0\\0\\-2\end{pmatrix} = \begin{pmatrix}2\\2\\-2\lambda \end{pmatrix},\quad \lambda\in[0,1]\,.\end{split}\]

Moreover, the sphere fulfills the equation

\[\left(\vec{X}-\vec{H}\right)^2 = 3^2 \quad\Leftrightarrow\quad {x_1}^2 + {x_2}^2 + {x_3}^2 = 9\,.\]

By plugging the equation for the edge into the equation for the sphere, we obtain

\[2^2+2^2+(-2\lambda)^2 = 9,\]

which can be solved for \(\lambda^2\):

\[\lambda^2 = \frac{1}{4}\]

Formally, this equation has the two solutions \(\lambda_1=+\frac{1}{2}\) and \(\lambda_2=-\frac{1}{2}\). Because on the edge, the parameter can only take values between \(0\) and \(1\), only the solution \(\lambda=+\frac{1}{2}\) is admissible. The coordinates of \(P\) are obtained by plugging this value into the equation describing the edge:

\[\begin{split}\vec{P} = \begin{pmatrix}2\\2\\-2\cdot \frac{1}{2} \end{pmatrix} = \begin{pmatrix}2\\2\\-1 \end{pmatrix}\end{split}\]

The point \(P\) hence has the coordinates \((2|2|-1)\).

Alternatively we can determine the intersection point with Sage: