12. Instrumenty syntetyczne

Tak jak światło składa się z elementów składowych tak i instrumenty finansowe składają się z instrumentów podstawowych. Jak już było wspomniane to na początku rozdziału o opcjach, opcje należą do tych składowych. Instrumenty syntetyczne to instrumenty składające (dające się rozłożyć) na składowe instrumenty. Instrumenty syntetyczne składają się z kombinacji dwu lub więcej elementów składowych. Oprócz opcji „cegiełkami” tworzacymi inne instrumenty są obligacje, akcje swapy. Konstruowanie takich instrumentów nazywane jest inżynierią finansową.

Zbudujmy portfel inwestycyjny. Kupujemy aktywo i od momentu posiadania aktywa obawiamy się spadku jego ceny i chcemy by wartość naszego portfela nie zmalała w przypadku spadku cen tego aktywa na rynku. Aby się zabezpieczyc przed spadkiem wartości portfela kupujemy opcje Put na wspomniane aktywo. Kupienie opcji Put i zapłacenie premii pozwala na ograniczenie możliwych strat z dołu przy zachowaniu szans na wzrost wartości aktywa. W takiej strategii widać podobieństwo do płacenia polisy ubezpieczeniowej za ograniczenie strat.

Istnieje strategia alternatywna dla opisanej sytuacji. Zamiast kupować aktywo i opcje Put zapewniającą „atrakcyjna” cenę jego sprzedaży możemy kupić jedynie opcje Call na „atrakcyjną” cenę aktywa. Zaoszczędzone pieniądze (różnica miedzy ceną kupna aktywa i premią opcji Put) możemy zainwestować w instrument dłużny oprocentowany stopą wolną od ryzyka. Jeśli wartość aktywa wzrośnie możemy kupić je wykorzystując opcje Call i swoją inwestycje. Jeśli wartość aktywa spadnie można pozwolić wygasnąć opcji i zachować pieniądze w inwestycji w stopę wolną od ryzyka.

Porównując obie strategie widzimy, że:

	Wartość przy wygaśnięciu
pozycja początkowa	\(S<K\)	\(S \geq K\)
Akcje + Put	\(K\)	\(S\)
Call + PV(K)	\(K\)	\(S\)

Niech cena aktywa wynosi \(S\) a cena wykonania opcji \(K\). W zależności od tego ile wynosi cena aktywa na rynku postępujemy:

w przypadku portfela:

Aktywo + Put

• Jeśli \(S < K\), wykorzystaj Put i weź \(K\)

• Jeśli \(S\geq K\), niech Put wygaśnie a masz \(S\)

Portfel Call + PV(K)

• \(PV(K)\) będzie warta \(K\) dla wygaśnięcia opcji

• Jeśli \(S < K\), niech Call wygaśnie a masz inwestycje, \(K\)

• Jeśli \(S\geq K\), wykorzystaj Call mając inwestycje i masz \(S\)

Jeśli te dwie pozycje są tyle samo warte na koniec inwestycji to powinny być tyle samo warte na początku inwestycji.

To prowadzi do warunku równości (parytetu) Put-Call

(1)\[S + P = C + PV(K)\]

Gdzie

• \(S\) - cena aktywa (1 akcji)

• \(P\) - cena opcji Put (1 opcja) na cenę wykonania \(K\) i czasie do wygaśnięcia \(T\)

• \(C\) - cena opcji Call (jedna opcja) na cene wykonania K i czasie do wygaśnięcia \(T\) - jak opcja Put.

• \(PV(K)\) - jedna obligacja (instrument dyskontowy) z wartością w czasie zapadalności T równej K.

Możemy również rozumieć ten związek jako konsekwencję matematycznej równości:

(2)\[\max (S-K,0) - \max (K-S,0) = S-K.\]

Prześledźmy, jeśli \(S>K\) to pierwszy składnik różnicy w równaniu (2) jest równy \(S-K\), a drugi jest zero. W przeciwnym przypadku \(K>S\) pierwszy się zeruje a drugi daje \(-(K-S)=S-K\) czyli w efekcie to samo co pierwszy. Funkcja wypłaty dla różnicy dwóch opcji - Call i Put, jest więc taka sama jak funkcja wypłaty dla posiadanej akcji i instrumentu dłużnego (obligacji) o wartość \(K\).

Funkcja wypłady zobowiązuje w czasie zapadalności obydwu opcji - czyli \(t=T\)). Wyobrażmy sobie, że jesteśmy w dowolnym momencie przed tym czasem, (niech będzie on oznaczony przez \(t=0\)). Wtedy cena akcji jest inna. Opcje przez ich czasem zapadalności możemy wycenić, np. za pomocą wzoru Blacka-Scholesa. Kredyt \(K\) będzie trzeba zdyskontować ze stopą wolną od ryzyka \(r\). Dlatego możemy się spodziewać, że będzie zachodził wzór:

\[S + P_P = P_C + e^{-rT} K,\]

gdzie przez \(P_C,P_P\) to ceny opcji Call i Put, odpowiednio, w czasie \(t=0\).

Wzór ten powinien zachodzić dla wycen opcji, sprawdźmy więc czy rzeczywiście tak jest. Możemy wykorzystać system algebry komputerowej by wykonał mozolną robotę za nas.

Poeksperymentuj z Sage!

Kod wykorzystujący CAS do pokazania spełnienia przez wzory Blacka-Scholesa parytetu Put-Call. Do sprawdzenia parytetu używamy polecenia bool, które próbuje algebraicznie udowodnić równość. Możemy też zobaczyć jawną postać lewej lub prawej strony równości używając do tego polecenia show, jednak uzyskane wzory mogą być dość długie, spróbuj sam!

Jeśli ten warunek nie zachodzi to mamy do czynienia z arbitrażem. Możliwość arbitrażu nie będzie istnieć długo, ale wtedy opłacalnym będzie działanie: Kup stronę „niską” a sprzedaj „wysoką”.

Arbitraż jest sytuacją wyjątkową i ulotną w stosunku do sytuacji gdy rynek jest w równowadze. Jeśli rynek jest efektywny (a raczej jest) używamy tego równania do znalezienia wielkości przy pomocy danych pozostałych trzech instrumentów

Informacja

Przykład

Z danych rynkowych widać, że:

• aktualna cena akcji = 50,

• cena opcji Put = 1.15, z ceną wykonania = 45,

• stopa wolna od ryzyka = 5%,

• Termin wygaśnięcia 1 rok

Pytanie: Jaka jest cena opcji Call?

Korzystając z równania parytetu mamy

\[50 1.15 = C + 45 / (1.05)\]

Czyli cena opcji Call wynosi C = 8.29

Przy wycenie opcji podobnie jak w wielu przypadkach instrumentów dłużnych stosuje ciągłą kapitalizacje w czasie.

Równania wartości pieniądza w czasie dla ciągłej kapitalizacji:

\[ \begin{align}\begin{aligned}PV = FVe^{-Rt}\\FV = PVe^{Rt}\end{aligned}\end{align} \]

Równanie pokazujące związek ceny akcji i opcji Call oraz Put i obligacji o stopie bez ryzyka (1) wygląda:

(3)\[ S + P = C + Ke^{-Rt}\]

Gdzie \(K\) - to wartość obligacji na stopę wolną od ryzyka na datę wygaśnięcia opcji. \(K\) to również cena wykonania opcji (obu) w czasie wygaśnięcia.

Równanie (3) nazwane parytetem call - put pokazuje symetrie ceny opcji put i call. Najlepiej można to prześledzić w przypadku opcji europejskich i aktywa nie wypłacającego dywidendy. Potraktujmy równanie (3) jako równość wartości dwu portfeli.

• Pierwszy portfel składa się z opcji call z ceną wykonania przykładowo 12 i obligacji która w chwili wygaśnięcia ma wartość aktywa w chwili wykonania. Obligacja obrazuje „pożyczone” środki pieniężne, które w chwili z wygaśnięcia musza być równe cenie wykonania aktywa pozwalając na wykonanie opcji.

• Drugi portfel składa się z opcji put z tą samą ceną wykonania jak opcja call i aktywa, które w chwili wykonania ma wartość ceny wykonania.

Istota parytetu zasadza się w równości tych dwu portfeli. Ta równość zachodzi niezależnie od ceny (wykonania) aktywa.

Sprawdźmy to:

Dla ceny aktywa 12 równość ta, wygląda następująco:

Call= 0	put = 0
Obligacja= 12	Aktywo =12
Wartość = 12	Wartość = 12

Call wygasa bez wartości gdy w chwili wygaśnięcia cena aktywa wynosi 12, podobnie put. Jednak zaciągnięty został kredyt o wartości 12.

Dla ceny aktywa 14 równość ta, wygląda następująco:

Call =2	put = 0
Obligacja= 12	Aktywo =14
Wartość = 14	Wartość = 14

Dla tej ceny aktywa opcja call ma wartość = 2 a opcja put wygasa bez wartości.

Dla ceny aktywa 6 równość ta, wygląda następująco:

Call= 0	put = 6
Obligacja= 12	Aktywo =6
Wartość = 12	Wartość = 12

Jak widać jeden portfel replikuje wartość drugiego bez względu na wartość aktywa. Są one równowartościowe.

Jeśli aktywo (akcja) wypłaca dywidendę to zachodzi równość.

cena opcji Put - cena opcji Call = present value ceny wykonania + present value dywidend - cena akcji

Gdy na wykresie zysków (strat) od ceny aktywa naniesiemy zależności dla ceny akcji opcji Call i Put możemy łatwo wykazać zależność parytetu graficznie.

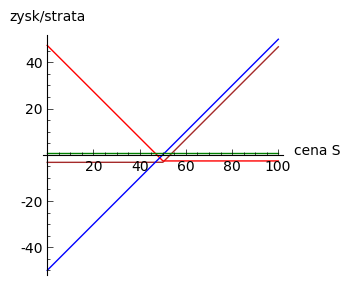
Oznaczenia:

Zółty kolor - long Call Czerwony - long Put Niebieski - pozycja długa w aktywie (akcja) Zielony - pozycja długa w obligacji.

Mając do dyspozycji równanie (1), możemy je rozwiązać na cenę opcji Call, cenę opcji Put lub cenę aktywa. Powyższe trzy możliwości mogą zostać wykorzystane do zastąpienia pozycji długiej lub krótkiej w portfelu. Razem daje to sześć możliwości zastosowania parytetu Put-Call, oraz tworzenia instrumentów syntetycznych.

12.1. Syntetyczny Put

Analogicznie aby określić cenę opcji Put przekształcamy wzór (1) do postaci:

(4)\[P = C - S + K e^{-Rt}\]

Co to oznacza? Kupienie opcji Call i sprzedaż aktywa (np. akcji) oraz kupienie obligacji o tym samym terminie zapadalności jak termin wygaśnięcia opcji (czyli \(T\)) replikuje wypłatę z zakupu opcji Put.

Graficznie wygląda to tak:

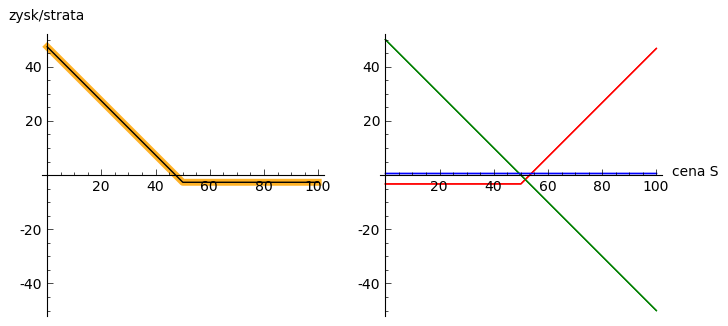
Syntetyczna opcja Put. Korzystając z parytetu put-call w postaci: \(P = C - S + K e^{-Rt}\) możemy za pomoca trzech instrumentów otrzymać taki sam efekt finansowy jak z instrumentu Put.

Na lewym panelu pomarańczowa gruba linia oznacza zależność zysku/straty z opcji Put. Na prawym panelu naniesiono trzy instrumenty z prawej strony równania (4). Dodając je do siebie otrzymujemy zysk/stratę całego portfela. Suma ta jest zaznaczona na wykresie lewym czarną linią. Widzimy, że pokrywa się ona zyskiem/stratą z opcji Put.

12.1.1. Krok po kroku

Zobaczmy jak to można samemu utworzyć powyższe wykresy. Po pierwsze zdefiniujmy z systemie Sage wypłaty opcji Put i Call oraz wzory Blacka-Scholesa:

Rozważmy aktywo o wartości chwilowej (cena spot ) \(S=50\) i zmienności (volatility) \(\sigma=0.5\). Ponadto, niech wolna od ryzyka stopa procentowa wynosi \(r=0.05\). Będziemy rozważać opcje o czasie wygaśnięcia trzy miesiące czyli \(T=90/365\). W chwili początkowej mamy następujące ceny opcji Call i Put, dane przez wzory Blacka-Scholesa:

Na ostatnim rysunku widzimy po prawej - profil zysku/straty dla poszczególnych instrumentów bazowych a po lewej czarną linią zaznaczono ich sumę - czyli nasz instrument syntetyczny. Szeroka różowa linia oznacza profil zysku straty dla opcji Call. Spełnienie parytetu powoduje, że obie linie się pokrywają.

Korzystając ze wzoru (1) możemy tworzyć instrumenty syntetyczne korzystając z czterech „cegiełek” wymienionych powyżej.

Poeksperymentuj z komputerem!

1. Przypuśćmy, że nie wycenilismy opcji Put wg. wzoru Blacka-Scholesa, tylko od kolegi, który zawsze ma odmienne od rynku zdanie, dowiedzieliśmy się, że \(P_p=5.94\). Przeprowadźmy te same obliczenia i zobaczmy czy parytet Put-Call dalej będzie spełniony!

2. Napisz własne programy rysujące pozostałe pięć instrumentów syntetycznych.

12.2. Syntetyczna pozycja Long Stock

Można stworzyć syntetyczną pozycję posiadania akcji poprzez kupienie Call, sprzedaż Put, i zainwestowanie ceny wykonania na stopę wolną od ryzyka do wygaśnięcia.

\[S = C - P + Ke^{-Rt}\]

Graficznie pokazuje to rysunek poniżej:

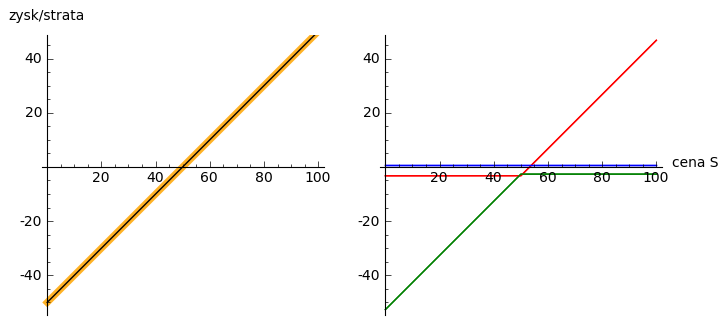
Parytet put-call: \(S = C - P + Ke^{-Rt}\)

12.3. Syntetyczny Long Call

Można zbudować pozycje syntetyczną long Call poprzez kupienie Put, kupienie akcji za pożyczoną kwotę równą cenie wykonania i spłacanej w chwili wygaśnięcia przy stopie wolnej od ryzyka.

\[C = P + S - Ke^{-Rt}\]

Na wykresie

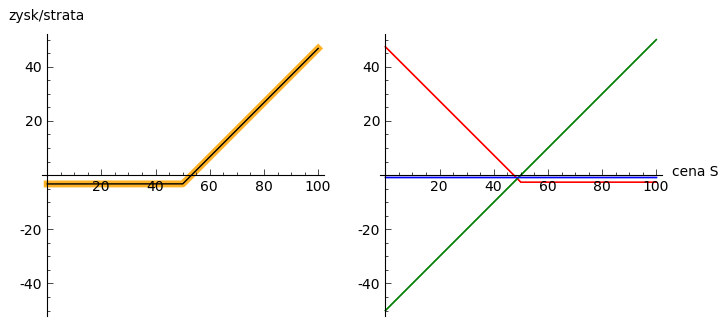
Parytet put-call: \(C = P + S - Ke^{-Rt}\)

12.4. Syntetyczna sprzedaż akcji

Można utworzyć syntetyczną pozycja sprzedaży akcji (short) poprzez sprzedaż Call, kupienie Put, kupienie obligacji (stopa wolna od ryzyka) za pożyczona cenę wykonania i trzymanie jej do zapadnięcia.

\[-S = P - C - Ke^{-Rt}\]

Graficznie

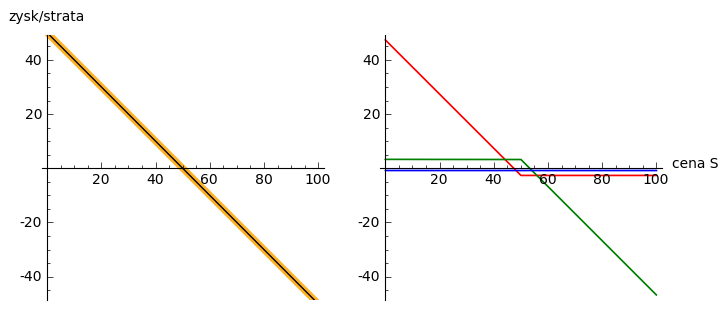
Parytet put-call: \(-S = P - C - Ke^{-Rt}\)

12.5. Syntetyczna pozycja short Put

Można stworzyć syntetyczną short Put poprzez sprzedaż opcji Call, kupno aktywa za kwotę pożyczoną na stopę wolna od ryzyka do wygaśnięcia.

\[-P = S - C - Ke^{-Rt}\]

Graficznie przedstawia wykres

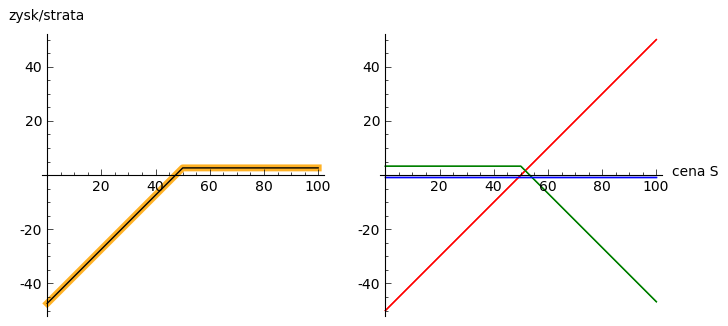
Parytet put-call: \(-P = S - C - Ke^{-Rt}\)

12.6. Przypadek kontraktów terminowych

Jeśli w miejsce kontraktów kasowych na aktywo wstawimy do równania parytetu kontrakty terminowe to otrzymamy podobne zależności dla rynku futures ( forward). W równości parytetu dla tego rynku opcje są opcjami dla kupna i sprzedaży kontraktu futures.

12.7. Podsumowanie

Równość zwana parytetem cen opcji call i put jest spełniona przy następujących warunkach:

1. Opcje są opcjami europejskimi

2. Cena wykonana jest identyczna dla opcji cal i opcji put.

3. Ceny transakcji są zerowe (tzw. Rynek bez tarcia)

4. Stopy procentowe są niezmienne aż do terminu wygaśnięcia.

5. Akcja nie wypłaca dywidendy.

Parytet put-call jest skutecznym narzędziem pozwalającym na testowanie modeli wyceny opcji. Jeśli sprawdzany model wyceny prowadzi do wyliczenia cen które nie spełniają parytetu na rynku bez arbitrażu, należy uznać go za błędny i go odrzucić ( albo jeszcze nad nim popracować by usunąć jego braki).

Parytet nie stosuje się do opcji amerykańskich jeśli są wykonywane przed dniem wygaśnięcia.

Wynika to z równań Blacka Scholes’a, które jest spełnione jeśli opcja nie zostanie wykonana przed wygaśnięciem. Amerykańskie opcje call i put nie spełniają warunków parytetu, ale spełniają słabszą relacje:

\[S_0 - K \leq C - P \leq S_0 - K e^{-Rt}\]

Warunek wypłacania dywidendy czyli warunek nr. 5 parytetu jest dość łatwy do ominięcia jeśli uwzględni sie wartość czasową wypłacanej dywidendy zanim opcja wygasnie. Wyniki takich wyliczeń, które polecamy do własnych wyliczeń można znaleźć:

W pracy Weiyu Guo i Tie Su-“ Option Put-Call Parity Relations When the Underlying Security Pays Dividends”- International Journal of Business and Economics, 2006, Vol. 5, No. 3, 225-230 albo http://moya.bus.miami.edu/~tsu/ijbe2006.pdf

12.8. Instrumenty syntetyczne

Kilka uwag o instrumentach syntetycznych.

Istnienie ich warunkuje ważność parytetu Call- Put. Do tego miejsca zajecie pozycji na rynku oznaczało kupno/sprzedaż aktywa lub kontraktu futures , kupno/sprzedaż opcji call lub put na dany instrument. Parytet call- put jest podstawą pewnego, nowego i innego spojrzenia na aktywo. Pozwala na tworzenie instrumentów rynkowych jako kombinacji innych instrumentów dających ten sam efekt i wartość dla inwestora.

Pozycja syntetyczna pozwala na osiągnięcie tego samego zysku( lub straty) co posiadanie instrumentu poprzez zajecie dwu innych pozycji na tym samym rynku. To jest często bardzo wygodne. Przykładowo, jeśli inwestor jest long call a chce być long put. Zamiast likwidować pozycję i otwierać nową, inwestor może zostać long call a sprzedać aktywo lub kontrakt futures jeśli na takim rynku działa. Zamiast więc dwu transakcji zawiera jedną i to dzięki temu przyjmuje syntetyczną pozycje long put. Innymi słowy inwestor „sfabrykował” syntetyczną pozycję dającą ten sam zysk jak long put posiadając opcje call i sprzedając aktywo (kontrakt futures).

Syntetyczne opcje muszą posiadać te same ceny wykonania i czasy wygaśnięcia, co jest konsekwencją założeń parytety call- put. Ponadto jeśli pozycja syntetyczna zawiera w sobie akcje i opcje, liczba akcji reprezentowanych przez opcje musi być równa ilości akcji.

Zalety instrumentów syntetycznych.

Instrumenty syntetyczne stwarzają w pewnych sytuacjach możliwości które mogą być atrakcyjne dla ich posiadacza.

1. Tworząc kontrakt syntetyczny wchodzimy w posiadanie instrumentu który nie istnieje inaczej niż wspomniany syntetyk.

2. W pewnych sytuacjach może być taniej kupić syntetyk niż instrument, który syntetyk „ naśladuje” ze względu na opłaty, prowizje, spready oraz wolumen który wymagany jest przy zakupie instrumentu „fizycznego’.

3. Często ( ale nie zawsze) syntetyki są mniej zmienne niż ceny instrumentów fizycznych.

4. Przykładem zalety syntetyka jest sytuacja krótkiej sprzedaży. Jeśli sprzedajemy krótko akcje nie musimy jej pożyczać i nie musimy się martwić o płatność dywidendy na sprzedaną krótko akcje.

Wydawać się może, że instrumenty syntetyczne pozwalają na większą spekulacje i pozwalają na uniknięcie depozytów zabezpieczających. Przykładowo może się wydawać, że w przypadku syntetycznego long/short futures można uniknąć płacenia depozytu zabezpieczającego. Niestety, pozycja short put wymaga tego samego depozytu jak pozycja short futures. Syntetyczna pozycja long futures wymaga wpłaty podobnego rzędu jak „fizyczna” pozycja długa na rynku kontraktów futures.

12.9. Swapy

Transakcje swapowe to syntetyczne instrumenty zbudowane z dwu podstawowych „cegiełek” instrumentów finansowych. Przykładowo są to połączenia instrumentu dłużnego o stałym oprocentowaniu z instrumentem dłużnym o zmiennym oprocentowaniu. Często do tej kombinacji instrumentów dochodzi transakcja wymiany walut.

Swapy stosuje się w celu unikania niedogodności związanych z wymiana walut, przeciwdziałaniu ryzyku kursowemu oraz zabezpieczenia się przed ryzykiem związanym z wahaniem stóp procentowych. Typowy podział swapów to podział na swapy kuponowe i bazowe.

12.9.1. Swap stopy procentowej

12.9.1.1. Swap kuponowy

Najbardziej typowy swap dotyczy wymiany płatności opartej na zmiennej stopie na płatność opartą o stopę stałą. Na ilustracji spółka A zgadza się wykonać płatność do spółki B liczoną w oparciu o zmienne oprocentowanie (np. LIBOR 6 - miesięczny) dla ustalonej kwoty. W zamian Spółka B zgadza się dokonać płatności odsetek od tej kwoty dla stałego oprocentowania ( np. 10% na rok) Wymiana płatności nastąpi co 6 miesięcy.

12.9.1.2. Swap bazowy

Dotyczy wymiany płatności opartych o zmienne oprocentowanie, ale dla różnych rodzajów stóp procentowych. W przypadku swapu bazowego strony wymieniają płatności oparte na jednym rodzaju zmiennej stopy procentowej( np. 3- miesięczny LIBOR) na inne płatności oparte o inną zmienną stopę oprocentowania. ( np. LIBOR 6- miesięczny).

SWAP jest transakcją zawieraną przez dwie strony. Podstawową trudnością dla instytucji chcącej zawrzeć transakcje tego typu jest znalezienie drugiej strony transakcji, czyli firmy chcącej również zawrzeć transakcje swap na warunkach atrakcyjnych. To stwarza nowe możliwości dla banków, które to pośredniczą w transakcjach i są stroną dla każdej części transakcji zawierając oddzielne kontrakty swap z obu stronami( klientami).

12.9.1.3. Swap stopy procentowej

Inaczej nazywany IRS (czyli interest rate swap). Polega ten swap na tym, że płatności wynikające dla stron z kontraktu swap dotyczą tego samego nominału kwoty, ale nie następuje tu żaden transfer tejże kwoty ani inna forma zmiany jej własności. Raczej mówi się o wymianie oprocentowania, ale nie wynika z tego, że następuje tu jakaś pożyczka.

Kontrakt swap reguluje okresowość płatności. Najczęściej są to okresy półroczne, ale mogą być i inne. Podstawą jest regulacja zawarta w kontrakcie. Chociaż strony umawiają się w kontrakcie co do dokonywania płatności w regularnych odstępach czasu to w praktyce, jednak, jest to każdorazowo, płatność jednej strony do drugiej równa różnicy zobowiązań.

Mechanizm swapu na stopę procentową.

Niech będą dwie firmy: Spółka A i spółka B. Spółka A funkcjonuje na rynku długo i jest uważana za spółkę o bardzo bezpiecznym bilansie i bezpiecznej działalności finansowej. Dla tego na rynku może otrzymać kredyt stało procentowy o stopie 8% lub zmienno procentowy w oparciu o WIBOR + 0,5%. Spółka B jest firma młodą i oferowany dla niej kredyt stało procentowy opiera się o stopę 10% albo kredyt o stopie zmiennej liczony według formuły WIBOR +1%.

Załóżmy że Spółka A, oczekując wzrostu stóp procentowych chce zaciągnąć kredyt o oprocentowaniu stałym, B zaś woli zaciągnąć kredyt o oprocentowaniu zmiennym.

W powyższej sytuacji:

Dla spółki A korzystne jest płacić 8% za kredyt o stałym oprocentowaniu a spółka B musi płacić WIBOR+0,5% za kredyt o zmiennym oprocentowaniu. I tak by było, gdyby nie istniał rynek swapów. Ale istnieje i firmy mogą we wzajemnym współdziałaniu poprawić sobie warunki kredytowania. Zawarcie kontraktu swap pomiędzy tymi dwoma firmami umożliwia poprawę sytuacji każdej z nich.

Na obu rynkach firma A ma lepsza sytuacje i otrzymuje lepsze propozycje, posiada bowiem bezwzględną przewagę na obu rynkach kredytowych. Na rynku stóp zmiennych spółka B za kredyt o zmiennym oprocentowaniu musi płacić tylko o 0,5% więcej niż firma A, która to na rynku kredytów procentowych otrzymuje warunki o 2% lepsze od spółki B. Tak wiec na rynku kredytów opartych o zmienna stopę firma B osiąga przewagę komparatywną.

Firmy zawierają kontrakt swap w ramach którego spółka B zaciąga kredyt według stopy WIBOR+1% i zobowiązuje się do płacenia stałej stopy 8.5% na rzecz A, w zamian to Spółka A zaciąga kredyt wg stopy stałej (8%) i zobowiązuje się do płacenia na rzecz B zmiennej stopy WIBOR. Czyli:

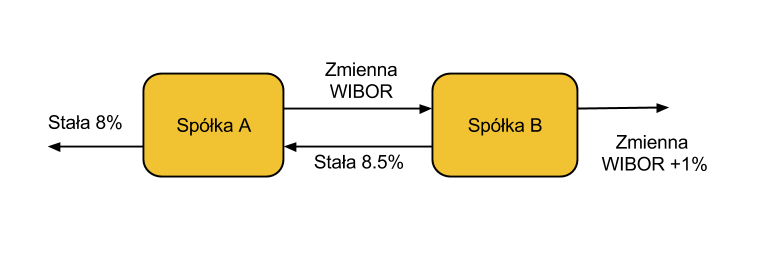
W wyniku zawartej transakcji Spółka B płaci:

• stałą stopę 8.5%

• (WIBOR+1%)

ale dostaje:

• +WIBOR

Czyli, w sumie płaci 9.5% odsetek wg stałej stopy procentowej. Dzięki zastosowaniu takiego swapu firma B zaoszczędza 0.5% w stosunku do stopy oferowanej przez kredytodawcę.

Natomiast spółka A płaci:

• stałą stopę 8%

• WIBOR

Lecz dostaje od spółki B:

• +stałą stopę 8.5%,

i w sumie płaci WIBOR-0.5% odsetek (zmienna stopa procentowa).

Dzięki zastosowaniu takiego swapu firma A zaoszczędza 1% w stosunku do stopy oferowanej przez kredytodawcę.

Analiza powyższego przykładu jest ilustracją ogólniejszej zasady. Podział zysków ze swapu może jest dowolny i negocjowany między partnerami swapu i zależy od ich porozumienia (warunków kontraktu), aczkolwiek ograniczony. Korzyść osiągana przez obie strony jest równa wartości różnicy stóp oferowanych firmom na rynku stóp stałych pomniejszonej o wartość różnicy stóp na rynku stóp zmiennych.

W naszym przypadku wartości te wynoszą 2%-0.5%=1.5%.

Natomiast w sytuacji gdy jedna z firm ma przewagę bezwzględną na jednym rynku a druga na drugim zysk będzie sumą wartość różnicy stóp oferowanym firmom na rynku stóp stałych powiększoną o wartość różnicy na rynku stóp zmiennych. W warunkach rynkowych przewaga komparatywna nie zawsze musi występować oraz ewentualne korzyści osiągane ze swapu mogą być zbyt małe w porównaniu do kosztów transakcji. Znalezienie drugiej strony swapu często jest trudne. Trudność tą usuwa pośrednik finansowy, którym najczęsciej jest bank, który to, niejako, staje się stroną dla obu stron swapu. Pośrednik przejmuje na siebie ryzyko związane z niedotrzymaniem warunków umowy przez każdego z kontrahentów (ryzyko kredytowe), oraz może przejmować na siebie część ryzyka walutowego (w swapach walutowych). Żąda w zamian wynagrodzenia- czyli każda ze stron rezygnuje na rzecz pośrednika z części beneficjów swapu.

Swap stopy procentowej ma podobną strukturę do kontraktu terminowego futures (forward) na stopę procentową, w tym sensie, że przyszłe zobowiązania swapu są określane dzisiaj.

12.9.2. Swap walutowy

W transakcji swapu walutowego ( currency swap), strony wymieniają waluty po ustalonym kursie. Następnie w określonych okresach dokonują wzajemnie płatności odsetkowych w oparciu o wcześniej ustalone pary stóp procentowych. Na koniec, dokonują powtórnej wymiany do oryginalnych walut w terminie zapadalności transakcji.

W każdym swapie walutowym występują trzy ważne składowe:

• Kwota główna

• Kurs wymiany

• Dwie stopy oprocentowania

Na początku swapu strony „wymieniają się” Kwotą Główną. Wymiana może być zarówno rzeczywista jak i „teoretyczna” (fizyczna wymiana nie ma miejsca). Kurs wymiany – kurs spot. Znaczenie kwoty głównej jest istotne dla określenia wielkości odsetek i wielkości wtórnej wymiany pod koniec transakcji swap. Końcowa wymiana następuje po kursie wymiany początkowej.

12.9.2.1. Walutowy swap kuponowy

Ten rodzaj swapu zwany powszechnie (currency coupon swap) ( cross currency interest rate swap) jest złożeniem swapu walutowego ze swapem stopy procentowej. Mechanizm swapu jest taki sam jak poprzednio. (Te same ruchy i zasady przepływu strumieni pieniężnych jak w swapie walutowym). Dodatkowo zamieniane jest oprocentowanie o stopie stałej na zmienna, lub odwrotnie.

Przykładowo: Dolarowy kredyt o stałej stopie odsetek zamieniany jest na kredyt w Euro o zmiennym oprocentowaniu.

12.9.3. Assets swap

Swap aktywów jest kombinacją aktywów i swapu, tak by stworzyć syntetyczne aktywa. Przykładowo: aktywo stałego oprocentowania może zostać zamienione w aktywo o zmiennym oprocentowaniu wyceniane w tej samej lub innej walucie.

Przykład:

Strony transakcji: Fundusz inwestycyjny i bank.

Fundusz inwestycyjny zamierza kupić na rynku: albo obligacje o stałym oprocentowaniu o rentowności 4 % rocznie, albo papier o zmiennym oprocentowaniu wyceniany na poziomie LIBOR.

Bank jest zainteresowany posiadaniem obligacji stałym oprocentowaniu równym 4 %, albo zamierza udzielić kredytu hipotecznego dla klienta na poziomie LIBOR + 0.5%. Fundusz kupuje obligacje i „swapuje” ją z bankiem, bez pośrednika.

Mechanizm swapu:

Fundusz:

• Kupuje obligacje o rentowności 4%

• Płaci do banku - 3,75%

• Otrzymuje z banku LIBOR

Czyli w wyniku otrzymuje: LIBOR +0,25

Bank:

• Udziela kredytu hipotecznego o oprocentowaniu LIBOR +0,5%

• Otrzymuje od Funduszu 3,75%

• Płaci do funduszu LIBOR

Czyli w sumie otrzymuje: 4,25%.

W wyniku transakcji swapu z funduszem Bank wykreował syntetyczną obligację stało procentową o oprocentowaniu wyższym niż rynek a fundusz syntetyczny papier dłużny zmienno procentowy o rentowności wyższej niż rynek.

12.9.4. Swap a kontrakt forward

Swap to umowa stron by wymienić się przepływami pieniężnymi w przyszłości. Umowa ta określa daty w których strumienie pieniężne będą płacone i sposób jak będą one liczone. Kontrakt forward jest przykładem prostego swapu. W przypadku kontraktu forward, następuje wymiana przepływów pieniężnych w danej, konkretnej dacie w przyszłości. W przypadku swapu przepływy występuje kilka razy w określonych datach w przyszłości. Czyli, …innymi słowy,… Możemy traktować swap jako syntetyczny portfel kontraktów forward na stopę procentową czyli Forward Rate Agreement (FRA).

12.9.5. Swap jako para obligacji

Jeśli kupujemy obligację, płacą nam odsetki. Jeśli emitujemy obligację, to my płacimy odsetki. W prostym swap’ie, robimy obie te rzeczy czyli płacimy stałe oprocentowanie fixed rate, nam płacą zmienne oprocentowanie, lub odwrotnie.

12.9.6. Forward Rate Agreement (FRA)

Transakcja FRA (opisana w skrypcie Rynki Finansowe) to terminowa transakcja stopy procentowej polegająca na ustaleniu w dniu jej zawarcia wysokości stopy procentowej dla przyszłego okresu odsetkowego (np. za 6 miesięcy) w odniesieniu do kwoty nominalnej, bez faktycznego jej zaangażowania. Zysk, bądź strata wynikają z różnicy pomiędzy stopą procentową transakcji, a właściwą dla danego okresu odsetkowego stawką referencyjną.

FRA są równoważne kontraktom forward w krótkoterminowych swap’ach stopy procentowej. FRA są syntetycznymi kontraktami swap kontraktów forward lub futures.

FRA jest umową stron aby wymienić się (swap) płatnościami wynikającymi ze stóp procentowych poprzez umówiony okres od pewnej daty w przyszłości. Jedna ze stron takiego kontraktu ustala sobie stałe oprocentowanie a druga zmienne. Kwota główna nie zostaje „przesuwana” między stronami, natomiast w dacie umowy jedna strona dokonuje wpłaty by skompensować drugiej stronie różnicę pomiędzy uzgodnionym oprocentowaniem a stopą spot w dniu zawarcia. Ilustracja funkcjonowania tego instrumentu została pokazana w skrypcie Rynki Finansowe.

Jeśli chcemy ustalić przyszłą stopę oprocentowania kredytu otrzymujemy zmienną a płacimy stałą (kupujemy FRA). Jeśli chcemy ustabilizować przyszła stopę inwestycji płacimy zmienną a otrzymujemy stałą (sprzedajemy FRA).

12.10. Swaption - swapcja

Wśród instrumentów finansowych służących do zarządzania ryzykiem stopy procentowej ważne miejsce zajmuje Swapcja (swaption). Jest to instrument finansowy, który jest opcją na zakup/sprzedaż swapu. Długa pozycja w opcji kupna daje prawo, ale nie obowiązek kupna swapu. Innymi słowy swapcja daje temu, kto ją posiada prawo (ale nie obowiązek) do zawarcia umowy swap’u z wystawcą swapcji. Warunki transakcji swap’u ustalone zostają w umowie swapcji. Warunki te określają: nominalna kwota główna wymiany, okresowość płatności stron (np. półrocznie, rocznie), płacone i otrzymywane stopy dla wymiany płatności, które to stopy określane są jako cena wykonania swapcji.

Podobne jak w przypadku opcji, swapcja może mieć cechy opcji europejskiej tzn. wykonanie w dacie wygaśnięcia, albo cechy opcji amerykańskiej- wykonalność w dowolnej dacie od zawarcia umowy do daty wygaśnięcia.

Swapcja typu amerykańskiego daje większą elastyczność w wyborze najlepszego czasu wykonania niż swapcja europejska co ma odbicie w cenie. Swapcje amerykańskie są znacznie droższe od europejskich.

Wysokość premii za swapcję jest ustalana między nabywcą a sprzedającym. Swapcja jest instrumentem OTC, czyli umową zawieraną pomiędzy bankiem specjalizującym się w transakcjach swap a klientem. Zależy ona od stóp procentowych, ich zmienności i czasu do wygaśnięcia. Data wygaśnięcia swapcji może wynosić i pięć lat od chwili zawarcia umowy ale typowe okresy ustalania stóp procentowych są między trzy a 12 miesięcy.

Przykład:

Firma z kraju Euro kupuje swapcje od Banku w dniu 23 października roku1, którą może wykonać w dowolnym czasie do 23 października następnego roku. Firma bowiem spodziewa się zawarcia transakcji kredytowej gdzieś w przyszłości do roku czasu i zamierza wejść w tym czasie w transakcje swapu płatności. Swap dotyczy kapitału w wysokości 100 milionów USD i terminu 5 lat. Firma zamierza zapewnić sobie płatności, powiedzmy, 1% stałego oprocentowania i otrzymywać zmienne w wysokości USD LIBOR, w sześciomiesięcznych płatnościach swapowych. Premia za swapcje wynosi, powiedzmy, 300 000 i jest płatna w EUR.

Przyczyna dla której firma kupiła swapcje to przewidywanie, że firma wejdzie ( lub może wejść) w umowę swapu kiedyś w ciągu roku. W ramach tej umowy zapewnia sobie płatności stało- procentowe na poziomie 1%by otrzymywać USD LIBOR. Taki poziom płatności byłby dla niej zadawalający. Chce więc zapewnić sobie takie warunki swapu, którego umowę chce zawrzeć w przyszłości. Obawia się jednak, że oprocentowanie stało procentowe może wzrosnąć zanim umowa swapu się rozpocznie. Płacąc premię za swapcje zabezpiecza sobie już dziś niższe płatności oprocentowania stałego.

Jeśli stopy wzrosną zanim firma będzie chciała zacząć swap to oprocentowanie stałe też wzrośnie wtedy firma wykorzysta swapcje i wejdzie w umowę swapu z bankiem płacąc 1% stałego procentowania a otrzymując stopę LIBOR w dolarach amerykańskich.

Jeśli stopy obniżą się to oprocentowanie stałe też będzie niższe i firma nie skorzysta ze swapcji wchodząc w umowę swapu na warunkach rynkowych płacąc niższą stopę stałą niż 1 % a otrzymując LIBOR w USD.

Dlaczego Bank wystawia swapcje?

Wystawiając swapcje bank bierze na siebie ryzyko, że w czasie od wystawienia swapcji do jej wygaśnięcia stopy procentowe mogą się zmienić w kierunku niekorzystnym i swapcja zostanie wykorzystana przez jej posiadacza. Gdy to się zdarzy wystawca swapcji jest zobowiązany do zawarcia kontraktu swapu na warunkach lepszych dla posiadacza swapcji niż aktualne warunki rynkowe.

W zamian za to ryzyko zyskuje premię za wystawienie swapcji. Wystawca opcji spodziewa się zysku z zawartych transakcji to znaczy, że premia za swapcje przewyższy straty na oprocentowaniu gdy posiadacz swapcji ją wykorzysta. Najwięcej zyskuje gdy swapcja nie zostaje wykonana (podobnie jak ma to miejsce w przypadku opcji).

Jeśli swapcja zostaje wykonana, czyli stopy procentowe wykonywane (wynikające z umowy swapcji) są bardziej korzystne dla posiadacza swapcji w stosunku do stóp na rynku swapów, to zyskiem posiadacza swapcji są niższe płatności oprocentowania albo wyższe przychody z oprocentowania w swapie. A jego stratą jest płacona za swapcje premia.

Należy podkreślić, że ryzyko wystawcy swapcji może być duże jeśli zmienność stóp procentowych na rynku jest znaczna, a nominał kapitału wielki. Załóżmy że swap dotyczy 100 milionów a posiadacz swapcji zamierza płacić 1% stałego otrzymując LIBOR w zamian. Gdy stopy na rynku swapów będą równe np. 2% skorzysta on z swapcji a jej wystawca będzie otrzymywał mniej niż stopy rynkowe stałe ( a pewnie i mniej niż LIBOR, który będzie płacił). Jego „ strata” w tym przypadku wyniesie 1% (2%-1%) roczne od kapitału czyli 1 milion rocznie. Jeśli stopy będą bardziej zmienne ( i wyniosą np. 3%) to rozmiar tej straty wyniesie 2 miliony. W przypadku dużej zmienności na rynku stóp procentowych premia za swapcje będzie też wyższa.

Swapcje stosuje się by zabezpieczyć swą ekspozycje na ryzyko stóp procentowych, w przypadku spodziewanego zawierania swapu w przyszłości. Swapcja gwarantuje najgorszy przypadek stóp dla swapu. Dla posiadacza swapcji, który chce płacić stałe oprocentowanie w swapie swapcja gwarantuje maksymalna stopę płatności. Dla posiadacza swapcji, który chce otrzymywać stała stopę , swapcja zabezpiecza minimalny poziom otrzymywanego oprocentowania.

Swapcja jest podobna do kontraktów caps i floor i collars w tym sensie, że są to też kontrakty opcyjnie na stopę procentową. Jednak w odróżnieniu od tych kontraktów są częściej stosowane ze wzgledu na lepsze dopasowanie do rynku swapów.