17. Dodatek: Komputerowa analiza drzew binarnych

Modele zachowania zmienającej się w czasie ceny pewnego aktywa \(S\), dzielą się na te z czasem ciągłym i dyskretnym. W przypadku modeli z czasem dyskretnym, zakładamy, że zmiany cen aktywa oraz wszelkie transakcje mają miejsce w pewnym wybranych momentach czasu, np. raz na dzień.

Najprostszym wariantem modelu z czasem dyskretnym, jest taki, w którym cena aktywa w czasie \(t+1\) może przybierać jedną z dwóch wartości:

\[\begin{split}S_{i+1} = \left\{ \begin{array}{l l} S^{+} & \quad \text{z prawdopodobieństwem} \; p\\ S^{-} & \quad \text{z prawdopodobieństwem} \; 1-p \end{array} \right.\end{split}\]

Startując z pewnej wartości aktywa w chwili początkowej, w pierwszym okresie mamy dwie możliwości. W drugim okresie, każda z tych możliwości prowadzi do kolejnych dwóch. Uogólniając po \(N\) okresach mamy \(2^N\) możliwych scenariuszy ewolucji ceny.

Wartości \(S^+\) \(S^-\) generalnie mogą być dowolne, ale z przyczyn praktycznych stosuje się kilka reguł. Po pierwsze wartość aktywa \(S_{i+1}\) zależy od poprzedniej wartości \(S_{i}\). Po drugie chcemy, żeby drzewo wartości aktywa generowane przez proces zmian cen w czasie było drzewem „rekombinującym”. Oznacza to, że jeśli aktywo zdrożeje a następnie potanieje to jego cena będzie dokładnie taka sama jakby najpierw potaniało a potem zdrożało. Wtedy, pomimo tego, że liczba scenariuszy po \(N\) okresach nadal pozostaje równa \(2^N\), to liczba możliwych do osiągnięcia różnych cen aktywa wynosie \(N+1\). Zdecydowanie ułatwia to wykonywanie rachunków na większych drzewach.

Następujące dwa scenariusze wyboru reguł zmian cen prowadzą do drzew rekombinujących.

• Drzewa addytywne: Jeśli cena aktywa po jednym okresie może wzrosnąć o \(\Delta_1\) lub zmaleć o \(\Delta_2\) i wartości te są stałe w czasie oraz niezależne od wartości ceny aktywa.

• Drzewa multiplikatywne: Jeśli cena aktywa po jednym okresie może wzrosnąć do \(S u\) lub zmaleć do \(S d\), dla pewnych liczb \(u>1\) oraz \(0<d<1\), niezależnych od ceny akcji i czasu.

Do operacji na drzewach użyjemy list zagnieżdżonych. Będziemy stosowali kilka funkcji pomocniczych, które będą generowały drzewa jak i przedstawiały je graficznie.

Opis programu

Funkcja gen_all generuje zadaną przez pierwszy parametr liczbę poziomów drzewa binarnego. Startujemy z wartości SP. Z danej wartości w poprzednim okresie są generowane dwie nowe. Zgodnie z regułą addytywną: s+delta1, s-delta2 a z multiplikatywną mamy (1+q)*s, s/(1+q). Reguła multiplikatywna jest domyśna, a funkcja użyje wersji addytynej jesli na wejsciu podamy parametry delta1,delta2. Struktura danych w której będziemy przechowywać dane wyjsciowe (drzewo binarne) to lista wartości w każdym okresie - czyli zagnieżdżona lista list. Ponieważ gen_all generuje wszystkie scenariusze należy pamiętać więc by \(n\) nie było zbyt duże, bo ilość scenariuszy jest \(\sim 2^n\).

Funkcja gen_recombining ma ten sam wywołania jak gen_all. Różnica polega na tym, że liczba możliwych stóp procentowych w n-tym okresie wynosi \(n+1\) a nie \(2 n\).

Funkcje plot_tree i plot_tree2 przedstawiają graficznie drzewa binarne, przy czym ta ostatnia wersja pozwala nanieść wartości z dodatkowego drzewa. Ma to zastosowanie w przypadku wizualizacji ewolucji cen opcji.

Drzewa multiplikatywne mają kilka zalet. Po pierwsze cena nie będzie ujemna. Nie jest to prawdą w modelu addytywnym! Po drugie, założenie stałej zmiany, niezależnej od ceny aktywa wydaje się nierzeczywiste. Rozsądniejszym wydaje się podanie względnej zmienności ceny aktywa, co właśnie implementuje model multyplikatywny.

Wygenerujmy dla przykładu drzewo z czterema rozgałęzieniami, rekombinujące i multiplikatywne:

Zauważmy, że w pełnym drzewie binarnym mamy w \(n\)-tym okresie \(2^n\) wartości, z których tylko \(n\) jest liczbowo różnych. Procedura rysująca wszystkie wartości, rysuje stopy procentowe w kółkach o kolorze jasnoszarym, przy czym jeżeli narysujemy więcej niż raz jasnoszare kółko jedno na drugim to kolor będzie ciemniejszy (związane jest to z opcją alpha=0.2, która określa stopnień przezroczystości koloru). Wynika z tego, że im ciemniejszy kolor tym więcej elementów pełnego drzewa dwumiennego ma daną wartość.

W pełnym drzewie binarnym istnieje tylko jedna ścieżką realizująca każdą gałąź. Wobec tego można powiedzieć, że liczba ścieżek realizujących stopę procentową jest proporcjonalna do odcienia na powyższym rysunku. Wyraźnie widzimy, że skrajne wartości są dużo mniej prawdopodobne od tych w środku.

Drzewa binarne, są fundamentalnym elementem modelowania rynku finansowego. Rozważania z zakresu teorii rynków finansowych mogą być łatwo zademnostrowane na rynkach skończonych, które są naturalnym rozszerzeniem rynku jednookresowego, dwustanowego.

17.1. Drzewa binarne

Rozważmy drzewo binarne w którym aktywo zmienia się począwszy od wartości początkowej \(S_0=100\) o 20 jednostek w górę lub w dół. Poniższy kod generuje takie drzewo:

sage: N = 3
sage: SP = gen_recombining(N,SP=100,delta1=20,delta2=20)
sage: plt_sp = plot_tree(SP)
sage: plt_sp.set_axes_range(ymax=170)
sage: plt_sp

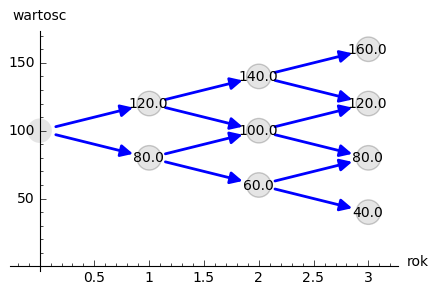
Możemy go samodzielnie uruchomić:

Mając drzewo w postaci struktury zagnieżdżonej listy, możemy wygenerować sobie wszystkie scenariusze ewolucji na tym drzewie:

Weźmy prawdopodobieństwa \(q\):

sage: var('q')
sage: q = 1/2
sage: Q = [q,1-q]

Wybierzmy sobie z naszego drzewa pewną cenę z okresu drugiego oraz dwie możliwości jej ewolucji w czasie.

sage: SP[2][1],SP[3][1],SP[3][2]
(100, 120, 80)

możemy sobie narysować to na drzewie, aby sprawdzić czy są to dokładnie te węzły o które nam chodzi.

sage: point([ (2,SP[2][1]),(3,SP[3][1]),(3,SP[3][2])],color='yellow',size=600,zorder=-10,ymin=0,ymax=170,xmax=3.4)+plt_sp

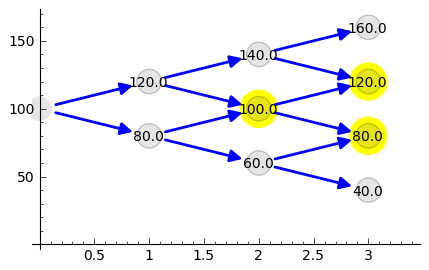
Dla prawdopodobieństwa \(q=\frac{1}{2}\) możemy obliczyć jaka będzie stopa oprocentowanie wolnego od ryzyka, które zapewni to, że nie będzie mógł zachodzić arbitraż (w podręcznikach matematycznych zwane jest ono też miarą arbitrażową):

sage: var('r')
sage: eq = SP[2][1]*(1+r) == q*SP[3][1]+(1-q)*SP[3][2]
sage: show(eq)

\[100 \, r + 100 = 100\]

Ile wynosi \(r\)?

sage: solve(eq,r)
[r == 0]

Bedzie to zachodziło dla każdego węzła, sprawdźmy:

sage: def calculate_r(i=2,j = 1):
...
...       eq = SP[i][j]*(1+r) == q*SP[i+1][j]+(1-q)*SP[i+1][j+1]
...       show([SP[i][j],SP[i+1][j],SP[i+1][j+1]])
...       return solve(eq,r)[0].rhs()

sage: calculate_r(i=1,j = 1)
0

\[\left[80, 100, 60\right]\]

Definiujemy tablicę wszystkich ścieżek (historii) ewolucji ceny aktywa, z notają, że:

• 0 - oznacza wzrost ceny

• 1 - oznacza spadek ceny

sage: all_moves = CartesianProduct(*( N*[[0,1]]) ).list()

Ruchom tym przyporządkowujemy prawdopodobieństwa. Korzystamy z faktu, że prawdopodobieństwa wzrostu lub spadku nie zależą od miejsca w drzewie w którym się znajdujemy.

sage: Qmoves = [ map(lambda x:Q[x],m) for m in all_moves ]

Możemy teraz obliczyć prawdopodobieństwo każdej ścieżki:

sage: map(prod,Qmoves)
[1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8]

Zobaczmy czy sumują się one do jedności:

sage: try:
...       print(  sum(map(prod,Qmoves)).full_simplify() )
sage: except:
...       print( sum(map(prod,Qmoves)) )
1

Jeśli dla każdej ścieżki obliczymy jej koncową wartość - biorąc pod uwagę rekombinacje to mamy po prostu sumę:

sage: map( sum, all_moves)
[0, 1, 1, 2, 1, 2, 2, 3]

To biorąc odpowiedznie prawdopodobieństwa zajścia ścieżek:

sage: map(prod,Qmoves)
[1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8]

Otrzymamy - Rozkład dwumianowy (Bernoulliego!)

sage: binom = (N+1)*[0]
sage: for m,p in zip( map( sum, all_moves), map(prod,Qmoves) ):
...       binom[m] += p
sage: binom
[1/8, 3/8, 3/8, 1/8]

sprawdźmy korzystając np. z jego implementacji w pakiecie scipy:

sage: import scipy.stats
sage: binom_dist = scipy.stats.binom(N,1-q)
sage: #bar_chart([binom_dist.pmf(x) for x in range(21)])
sage: d = [binom_dist.pmf(x) for x in range(N+1)]
sage: d
[0.12500000000000003, 0.375, 0.375, 0.12500000000000003]

Możemy teraz obliczyć średnią z ceny aktywa po ścieżkach:

sage: for q_,p_,in zip(Qmoves,all_paths):
...       print( q_,p_,round( prod(q_)*SP[N][p_[N]] ) )
[1/2, 1/2, 1/2] [0, 0, 0, 0] 20
[1/2, 1/2, 1/2] [0, 0, 0, 1] 15
[1/2, 1/2, 1/2] [0, 0, 1, 1] 15
[1/2, 1/2, 1/2] [0, 0, 1, 2] 10
[1/2, 1/2, 1/2] [0, 1, 1, 1] 15
[1/2, 1/2, 1/2] [0, 1, 1, 2] 10
[1/2, 1/2, 1/2] [0, 1, 2, 2] 10
[1/2, 1/2, 1/2] [0, 1, 2, 3] 5

Średnia wartość aktywa \(S\) wynosi:

\[\sum_{p\in P}\left (\prod q_i \right )SP_{N,p_N}\]

gdzie oznaczyliśmy przez dla ścieżki \(p\) ze zbioru wszystkich scieżek \(P\) przez:

• \(q_i\) - prawdopodobieństwo, skoku ceny między okresami \(i\) i \(i+1\)

• \(p_N\) - indeks w drzewie wartości aktywa na końcu ścieżki \(p\)

• \(SP_{i,j}\) jest tablicą cen aktywa, w \(i\) oznacza okres a \(j\) indeks w drzewie wartości.

Na przykład mamy:

sage: sum([prod(q_)*SP[N][p_[N]] for q_,p_,in zip(Qmoves,all_paths)])
100

Mając takie narzędzie możemy policzyć średnią po realizacjach (ścieżkach) dowolnej funkcji ceny aktywa. Na przykład akcji sprzedaży, której cena jest dana przez: \(\max(0,S-K)\)

sage: K=100
sage: sum([prod(q_)*( max(0,SP[N][p_[N]]-K) ) for q_,p_,in zip(Qmoves,all_paths)])
15

17.1.1. Ewolucja portfela na drzewie binarnym.

Mamy portfel \(P\) - [liczba akcji, liczba obligacji] w chwili \(t=0\). Obliczmy jego ewolucję czasową. Zanim to uczynimy, policzmy jak zmienia się cena aktywa na pewnej ścieżce:

sage: for i,p_ in enumerate(all_paths[6]):
...       print( "czas:",i,"cena",SP[i][p_] )
czas: 0 cena 100
czas: 1 cena 80
czas: 2 cena 60
czas: 3 cena 80

co graficznie możemy przedstawić:

sage: plot_tree(SP)+line( [( i,SP[i][p_] ) for i,p_ in enumerate(all_paths[6])],color='red')

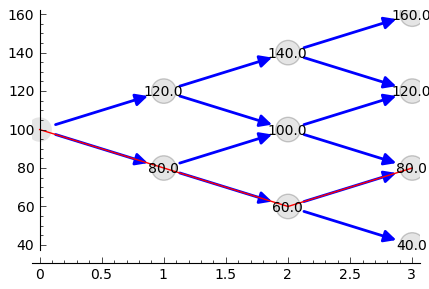
sage: r = 0
sage: P = [1,123]
sage: for i,p_ in enumerate(all_paths[6]):
...       print(  "czas:",i,"cena",SP[i][p_],"wartość portfela:",P[0]*SP[i][p_]+P[1]*(1+r)^i )
czas: 0 cena 100 wartość portfela: 223
czas: 1 cena 80 wartość portfela: 203
czas: 2 cena 60 wartość portfela: 183
czas: 3 cena 80 wartość portfela: 203

sage: K=100
sage: [prod(q_)*( max(0,SP[N][p_[N]]-K) ) for q_,p_,in zip(Qmoves,all_paths)]
[15/2, 5/2, 5/2, 0, 5/2, 0, 0, 0]

sage: [max(0,s-K) for s in SP[N]]
[60, 20, 0, 0]

sage: OP = [ [max(0,s-K) for s in SP[N]] ]

sage: OP
[[60, 20, 0, 0]]

17.1.2. Hedging na drzewie binarnym:

Przypuścmy, że mamy kupca na opcję po 16, której cena godziwa, tzn. taka przy której nie zachodzi arbitraż, wynosi 15. Istnieje możliwość zarobienia. Wystawiając jednak opcje narażamy się na duże ryzyko. Na naszym modelowym rynku idealnym jesteśmy zainteresowani zyskiem bez ponoszenia ryzyka.

Ideą hegdingu, jest taka konstrukcja portfelem by w KAŻDYM scenariuszu ewolucji ceny aktywa, otrzymać zysk = 1 (wynikający z początkowej różnicy ceny godziwej i rynkowej).

Po pierwsze będziemy potrzebowali ceny opcji w każdym węźle drzewa. Niech drzewo cen opcji będzie w strukturze zagnieżdzonej listy OP.

sage: OP = [ [max(0,s-K) for s in SP[N]] ]
sage: for idx in range(N):
...       el = [ q*OP[-1][i]+(1-q)*OP[-1][i+1] for i in range(len(OP[-1])-1)]
...       OP.append(el)
sage: OP.reverse()

sage: plot_tree2(SP,OP)

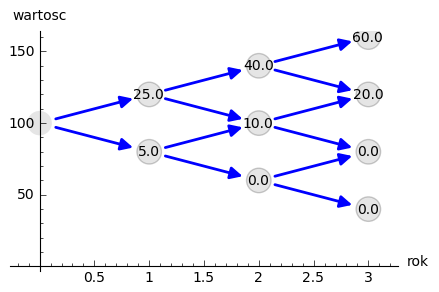
sage: OP
[[15], [25, 5], [40, 10, 0], [60, 20, 0, 0]]

sage: p_ = all_paths[6]
sage: p_
[0, 1, 2, 2]

sage: p_ = [0,0,1,2]
sage: Pt = [(0,16,SP[0][0])]
sage: for i,(k,k_next) in enumerate(zip(p_,p_[1:])):
...       delta = (OP[i+1][k]-OP[i+1][k+1])/(SP[i+1][k]-SP[i+1][k+1])
...       x = delta - Pt[-1][0]
...       print(  k,delta,Pt[-1][0] )
...       Pt.append( (delta,Pt[-1][1]-x*SP[i][k],SP[i+1][k_next]) )
0 1/2 0
0 3/4 1/2
1 1/2 3/4

sage: Pt
[(0, 16, 100), (1/2, -34, 120), (3/4, -64, 100), (1/2, -39, 80)]

sage: Pt[-1][0]*Pt[-1][2],Pt[-1][1]
(40, -39)

sage: print( "mamy akje szt.:",Pt[-1][0],"po",Pt[-1][2] )
sage: print( "oraz depozyt/dlug:",Pt[-1][1] )
sage: print( "i obiecankę za opcję:",-max( Pt[-1][2]-K,0) )
mamy akje szt.: 1/2 po 80
oraz depozyt/dlug: -39
i obiecankę za opcję: 0

sage: total = Pt[-1][0]*Pt[-1][2]+Pt[-1][1]-max( Pt[-1][2]-K,0)
sage: total
1

sage: def calculate_evo(SP,OP,p_,c=1):
...       Pt = [(0,0,SP[0][0])]
...       for i,(k,k_next) in enumerate(zip(p_,p_[1:])):
...           delta = c*(OP[i+1][k]-OP[i+1][k+1])/(SP[i+1][k]-SP[i+1][k+1])
...           delta = 3.0 ## try -1 0
...           x = delta - Pt[-1][0]
...           Pt.append( (delta,Pt[-1][1]-x*SP[i][k],SP[i+1][k_next]) )
...       return (Pt[-1][0]*Pt[-1][2]+Pt[-1][1]-max(c*( Pt[-1][2]-K),0),Pt)

sage: def calculate_evo(SP,OP,p_,c=1):
...       Pt = [(0,0,SP[0][0])]
...       for i,(k,k_next) in enumerate(zip(p_,p_[1:])):
...           delta = c*(OP[i+1][k]-OP[i+1][k+1])/(SP[i+1][k]-SP[i+1][k+1])
...           x = delta - Pt[-1][0]
...           Pt.append( (delta,Pt[-1][1]-x*SP[i][k],SP[i+1][k_next]) )
...       return (Pt[-1][0]*Pt[-1][2]+Pt[-1][1]-max(c*( Pt[-1][2]-K),0),Pt)

sage: calculate_evo(SP,OP,[0,0,1,2])[0]
-15

sage: for path in all_paths:
...       print( SP[-1][path[-1]],calculate_evo(SP,OP,path)[0],-max(SP[-1][path[-1]]-K,0) )
160 -15 -60
120 -15 -20
120 -15 -20
80 -15 0
120 -15 -20
80 -15 0
80 -15 0
40 -15 0

17.1.3. Niezerowa stopa procentowa

Pomińmy teraz nierealistyczne założenie o niezerowej stopie procentowej.

max(0,K-s) - czyli mamy do czynienia z opcją sprzedaży

sage: rate = 28.59
sage: (1+rate/3/100).n(),exp(rate/3/100).n()
(1.09530000000000, 1.09998880227224)

sage: C = exp(rate/3/100).n()
sage: C
1.09998880227224

sage: C=1.1

Generujemy drzewko prawdopodobieństw arbitrażowych:

sage: QP = []
sage: for k in range(N):
...       q_ = [ (sp*C-sp1)/(sp0-sp1) for j,(sp,sp0,sp1) in enumerate(zip(SP[k],SP[k+1
sage: ],SP[k+1][1:]))]
...          # print( k,j,sp,sp0,sp1,(sp*C-sp1)/(sp0-sp1) )
...       QP.append(q_)

sage: QP
[[0.750000000000000], [0.800000000000000, 0.700000000000000], [0.850000000000000, 0.750000000000000, 0.650000000000000]]

sage: plot_tree(SP)

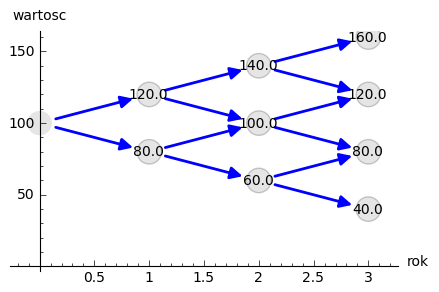
Generacja drzewka prawdopodobienstw \(q=q_t\)

sage: K = 100
sage: OP = [ [max(0,K-s) for s in SP[N]] ]
sage: for idx in range(N):
...       el = [ 1/C*(QP[N-idx-1][i]*OP[-1][i]+(1-QP[N-idx-1][i])*OP[-1][i+1]) for i in range(len(OP[-1])-1)]
...       OP.append(el)
sage: OP.reverse()

sage: plt=plot_tree2(SP,OP)
sage: plt.set_axes_range(ymax=170.0)
sage: plt += line([(0,100),(3,100* exp(rate/100))],color='red')
sage: plt += line([(i,100*(1+rate/3/100.)^i) for i in range(4)],color='green')
sage: plt

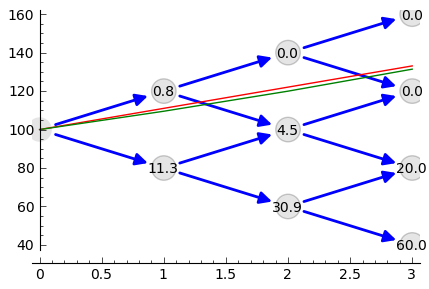
sage: OP
[[3.13673929376408], [0.826446280991734, 11.3223140495868], [0.000000000000000, 4.54545454545454, 30.9090909090909], [0, 0, 20, 60]]

sage: q= 0.657756377113472
sage: 1/C*(q*20+(1-q)*60)
30.6270408322374

sage: plot_tree(SP)

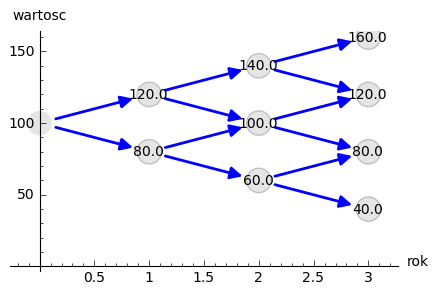
sage: path = [0,0,0,1]
sage: path = [0, 0, 1, 2]
sage: plt =  plot_tree2(SP,OP)
sage: plt += line( [( i,SP[i][p_] ) for i,p_ in enumerate(path)],color='red')
sage: plt.set_axes_range(xmin=-1)
sage: plt

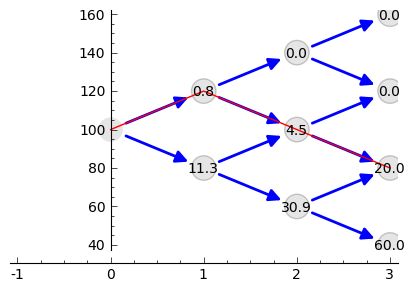
sage: def calculate_evo(SP,OP,p_,c=1,rate=28.59,depozyt=0):
...       """ Zwraca zysk/strate na zabezpieczeniu pozycji opcji P/C technika delta-hegde
...
...       :param SP: drzewo cen akcji
...       :param SP: drzewo cen opcji
...       :param c: 1 - dla wystawienia opcji, -1 - dla kupna opcji
...       """
...       C = exp(rate/3/100).n()
...       Pt = [(0,depozyt,SP[0][0])]
...       for i,(k,k_next) in enumerate(zip(p_,p_[1:])):
...           delta = c*(OP[i+1][k]-OP[i+1][k+1])/(SP[i+1][k]-SP[i+1][k+1])
...           x = delta - Pt[-1][0]
...           #print( delta,x,-x*SP[i][k] )
...           Pt.append( (delta,C*( Pt[-1][1]-x*SP[i][k]),SP[i+1][k_next]) )
...       return (Pt[-1][0]*Pt[-1][2]+Pt[-1][1]-c*max(c*( Pt[-1][2]-K),0),Pt)

sage: [SP[i][k] for i,k in enumerate(path)]
[100, 120, 100, 80]

sage: calculate_evo(SP,OP,path,c=-1,rate=28.59)[1]
[(0, 0, 100), (0.262396694214876, -28.8633425389616, 120), (0.113636363636363, -12.1131898459641, 100), (1/2, -55.8239405508766, 80)]

sage: calculate_evo(SP,OP,path,c=-1,rate=28.59)[0]
4.17605944912340

Załóżmy, że kupiliśmy opcję za 2.5, wtedy mamy depozyt=2.5:

sage: calculate_evo(SP,OP,path,c=-1,rate=28.59,depozyt=-2.5)[0]*exp(-rate/100)
0.637631093519873

Wartość opcji w czasie \(t=3\) wynosi:

sage: (OP[0][0])*1.1^3
4.17499999999999

Efekt zabezpieczenia - każdy scenariusz prowadzi do tego samego wyniku finansowego.

sage: for path in all_paths:
...       print( path,SP[-1][path[-1]],calculate_evo(SP,OP,path,c=-1,rate=28.59)[0] )
[0, 0, 0, 0] 160 4.17544866397274
[0, 0, 0, 1] 120 4.17544866397274
[0, 0, 1, 1] 120 4.17605944912340
[0, 0, 1, 2] 80 4.17605944912340
[0, 1, 1, 1] 120 4.17667022805639
[0, 1, 1, 2] 80 4.17667022805639
[0, 1, 2, 2] 80 4.17707741815681
[0, 1, 2, 3] 40 4.17707741815681

Widzimy, że dla każdego scenariusza mamy ten sam stan końcowy!

sage: exp(0.1/sqrt(3))^3
e^(0.100000000000000*sqrt(3))