Linear Transformations

Theorem 1. \(\\\)

Let \(\,V\ \) and \(\,W\ \) be vector spaces over a field \(\,K,\ \ F\in\text{Hom}(V,W).\) \(\\\) The transformation \(\,F\ \) is an injective mapping if and only if

\[\text{Ker}\,F\,=\,\{\,\theta_V\}\,,\qquad\text{that is}\qquad\text{def}\,F = 0\,.\]

Proof and discussion.

A tranformation \(\;F\;\) is injective \(\,\) if distinct arguments are mapped to distinct images:

\[v_1\neq v_2\qquad\Rightarrow\qquad F(v_1)\neq F(v_2)\,,\qquad v_1,v_2\in V\,.\]

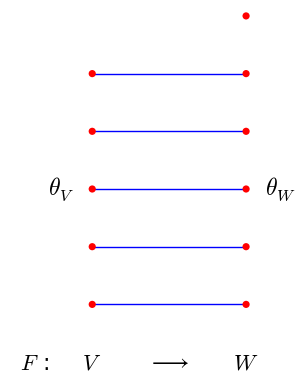
Image of the space \(\;V\;\) under the transformation \(\;F\;\) may be (as in the diagram above) a proper subset of the space \(\;W:\ \ \text{Im}\,F\equiv F(V)\subsetneq W\,,\ \) but each element \(\;w\in\text{Im}\,F\ \) corresponds to exactly one element \(\;v\in V,\ \) the one whose image is \(\;w.\)

Kernel of the transformation \(\;F\in\text{Hom}(V,W)\ \) is by definition a set of those vectors of the space \(\;V,\ \) whose image is the zero vector of the space \(\;W,\ \) and the defect of \(\;F\ \) is equal to dimension of the kernel:

\[\text{Ker}\,F\,=\,\{\,v\in V:\ F(v)=\theta_W\}\,,\qquad\text{def}\,F\,=\,\dim\,\text{Ker}\,F\,.\]

\(\;\Rightarrow\,:\ \) Assume that \(\;F\ \) is injective. Then the zero vector \(\;\theta_W\ \) of the space \(\;W\ \) is an image only of the zero wector \(\;\theta_V,\ \) which means that \(\ \,\text{Ker}\,F=\{\,\theta_V\}\ \) and \(\ \text{def}\,F=0\,.\)

\(\;\Leftarrow\,:\ \) Assume that \(\;F\ \) is not injective. \(\\\) Then there are two disctinct vectors \(\;v_1\ \,\) and \(\ v_2,\ \) which under the transformation \(\;F\ \) have the same image:

\[ \begin{align}\begin{aligned}v_1\neq v_2\quad\land\quad F(v_1)\,=\,F(v_2)\,,\\\qquad\text{that is}\qquad v_1-v_2\neq\theta_V\quad\land\quad F(v_1)-F(v_2)=F(v_1-v_2)=\theta_W.\;\end{aligned}\end{align} \]

Hence, \(\ \,\theta_V\neq v_1-v_2\in\text{Ker}\,F,\ \,\) and thus \(\ \,\text{Ker}\,F\neq\{\,\theta_V\}\ \) and \(\ \text{def}\,F\neq 0\,.\)

By contraposition we deduce that if \(\ \text{def}\,F=0,\ \) then \(\ F\ \) is injective.

Theorem 2.

Tranformation \(\,F\in\text{Hom}(V,W)\,\) preserves linear independence of any set of vectors of the space \(\,V\,\) if and only if it is injective

Proof bases on the \(\,\) (previous) \(\,\) theorem, which states that injectivity of the transformation \(\ F\ \) is equivalent to vanishing of the defect

\(\;\Rightarrow\,:\ \) Assume that \(\;F\ \) is not injective.

Then \(\ \text{def}\,F=\dim\,\text{Ker}\,F=k>0.\ \) Let \(\,\mathcal{U}=(\,u_1,\,u_2,\,\dots,\,u_k)\ \) be a basis of \(\,\text{Ker}\,F.\ \) The set \(\,\mathcal{U}\ \) is linearly independent, but its image under the transformation \(\,F:\)

\[F(\mathcal{U})\,=\,(\,Fu_1,\,Fu_2,\,\dots,\,Fu_k\,)\,=\, (\,\theta_W,\,\theta_W,\,\dots,\,\theta_W)\]

is, of course, linearly dependent (actually, it is maximally linearly dependent).

Hence, if \(\,F\ \) is not injective, then there are sets of vectors whose linear independence is not preserved under the transformation \(\,F.\,\) On the other hand, if the transformation \(\,F\,\) preserves linear independence of any set of vectors, then it is injective.

\(\;\Leftarrow\,:\ \) Assume that \(\;F\ \) is injective, \(\,\) that is \(\;\text{Ker}\,F=\{\,\theta_V\}\,.\)

Consider a linearly independent set \(\;(x_1,\,x_2,\,\dots,\,x_r)\ \) of vectors of the space \(\,V.\,\) \(\\\) Then \(\,\) for \(\,a_1,\,a_2,\,\dots,\,a_r\in K:\)

\[\begin{split}\begin{array}{rcc} \text{if} & \qquad & a_1\,Fx_1\,+\,a_2\,Fx_2\,+\,\ldots\,+\,a_r\,Fx_r\,=\,\theta_W\,, \\ \\ \text{then:} & \qquad & F(a_1\,x_1+\,a_2\,x_2+\ldots+\,a_r\,x_r)\,=\,\theta_W\,, \\ & \qquad & a_1\,x_1+a_2\,x_2+\ldots+a_r\,x_r\in\text{Ker}\,F\,, \\ & \qquad & a_1\,x_1\,+a_2\,x_2\,+\ldots+\,a_r\,x_r\,=\,\theta_V\,, \\ & \qquad & a_1=\,a_2=\,\dots\,=\,a_r=0\,. \end{array}\end{split}\]

Hence, the vectors \(\ Fx_1,\,Fx_2,\,\dots,\,Fx_r\ \) are also linearly independent.

In this way we proved that for any vectors \(\ \,x_1,\,x_2,\,\dots,\,x_r\,\in V\ \) we have the implication (l.i. = linearly independent):

\[(\,x_1,\,x_2,\,\dots,\,x_r)\ \ \ \ \text{l.i.} \qquad\Rightarrow\qquad (\,Fx_1,\,Fx_2,\,\dots,\,Fx_r)\ \ \ \ \text{l.i.}\]

which means precisely that \(\,F\ \) preserves linear independence of any set of vectors.

Corollaries and discussion. \(\,\) Consider an \(\,n\)-dimensional vector space \(\,V(K)\ \) with basis \(\,\mathcal{B}=(v_1,\,v_2,\,\dots,\,v_n).\ \) The mapping

\[\begin{split}I_{\mathcal{B}}:\quad V\,\ni\, x\,=\,\sum_{i\,=\,1}^n\ a_i\,v_i \quad\rightarrow\quad I_{\mathcal{B}}(x)\,:\,=\, \left[\begin{array}{c} a_1 \\ a_2 \\ \dots \\ a_n \end{array}\right] \,\in\,K^n\end{split}\]

which transforms a vector \(\,x\ \) into a column of coordinates of this vector in basis \(\,\mathcal{B}\ \) is an isomorphism of the space \(\,V\ \) onto the space \(\,K^n,\ \) and thus it is injective. Hence, \(\,I_{\mathcal{B}}\ \) preserves linear independence of vectors. The same property holds for the inverse transformation, which is also an isomorphism.

Consider a set \(\,(x_1,\,x_2,\,\dots,\,x_r)\ \) of vectors, where

\[\begin{split}x_j\,=\;\sum_{i\,=\,1}^n\ a_{ij}\,v_i\,, \qquad\text{so that}\qquad I_{\mathcal{B}}(x_j)\,=\, \left[\begin{array}{c} a_{1j} \\ a_{2j} \\ \dots \\ a_{nj} \end{array}\right] \,,\quad j=1,2,\dots,r.\end{split}\]

The aforementioned property of the isomorphisms \(\ I_{\mathcal{B}}\ \) and \(\ I_{\mathcal{B}}^{-1}\ \) implies that \(\,\) (l.i. = linearly independent):

\[(\,x_1,\,x_2,\,\dots,\,x_r)\ \ \ \ \text{l.i.} \qquad\Leftrightarrow\qquad \left(\; I_{\mathcal{B}}(x_1),\,I_{\mathcal{B}}(x_2),\,\dots,\,I_{\mathcal{B}}(x_r)\; \right) \ \ \ \ \text{l.i.}\]

Corollary 1a.

Vectors from an \(\,n\)-dimensional vector space \(\,V(K)\ \) are linearly independent if and only if columns of their coordinates \(\,\) (as vectors of the space \(\,K^n\)) \(\,\) are linearly independent in every basis of the space \(\,V.\)

Since linear dependence is a negation of linear independence, we may also write \(\,\) (l.d. = linearly dependent):

\[(\,x_1,\,x_2,\,\dots,\,x_r)\ \ \ \ \text{l.d.} \qquad\Leftrightarrow\qquad \left(\; I_{\mathcal{B}}(x_1),\,I_{\mathcal{B}}(x_2),\,\dots,\,I_{\mathcal{B}}(x_r)\; \right) \ \ \ \ \text{l.d.}\]

Corollary 1b.

Vectors from an \(\,n\)-dimensional vector space \(\,V(K)\ \) are linearly dependent if and only if columns of their coordinates \(\,\) (as vectors of the space \(\,K^n\)) \(\,\) are linearly dependent in every basis of the space \(\,V.\)

If \(\,r=n,\ \) then the columns of coordinates form a square matrix

\[\boldsymbol{A}\ =\ [\,a_{ij}\,]_{n\times n}\ =\ [\,I_{\mathcal{B}}(x_1)\,|\,I_{\mathcal{B}}(x_2)\,|\,\dots\,|\,I_{\mathcal{B}}(x_n)\,]\,.\]

An element \(\,a_{ij}\ \) of this matrix is the \(\,i\)-th coordinate of the \(\,j\)-th vector from the set \(\,(x_1,\,x_2,\,\dots,\,x_n).\ \\\) Properties of determinant imply

\[(\,x_1,\,x_2,\,\dots,\,x_n)\ \ \ \ \text{l.i.} \qquad\Leftrightarrow\qquad \det\,\boldsymbol{A}\neq 0\,.\]

Corollary 2.

In an \(\,n\)-dimensional vector space \(\,V(K)\ \) a set of \(\,n\ \) vectors is linearly independent if and only if the determinant of the matrix formed from the coordinates of these vectors is non-zero.

Taking into account that in an \(\,n\)-dimensional vector space every set of \(\,n\ \) linearly independent vectors comprises a basis, \(\,\) we may formulate

Corollary 3.

In an \(\,n\)-dimensional vector space \(\,V(K)\ \) a set of \(\,n\ \) vectors compises a basis of this space if and only if the determinant of the matrix formed from the coordinates of these vectors is non-zero.