Inner (Scalar) Product

Axiomatic Definition and its Implementations

Definition.

Let \(\,V(C)\ \) be a vector space.

An inner product is a map \(\,f:\ V\times V\rightarrow C\ \) satisfying the conditions

(and denoted \(\,f(x,y)=\langle x,y\rangle,\ \ x,y\in V\)) :

1. \(\,\langle y,x\rangle\,=\,\langle x,y\rangle^*\,,\)

2. \(\,\langle\,x,\,y_1+y_2\,\rangle\,=\,\langle x,y_1\rangle\,+\,\langle x,y_2\rangle\,,\)

3. \(\,\langle x,\,\alpha\,y\rangle\,=\,\alpha\,\langle x,y\rangle\,,\quad\alpha\in C\,,\)

4. \(\,\langle x,x\rangle\geq 0\quad\land\quad [\ \,\langle x,x\rangle=0\ \ \Leftrightarrow\ \ x=\theta\ \,]\,.\)

Comments and remarks.

• An inner product of two vectors belonging to the complex space \(\,V\ \) is a complex number.

• The condition 1. states that swapping of vectors is equivalent to complex conjugation of an inner product. If \(\ y=x,\ \) then: \(\ \langle x,x\rangle=\langle x,x\rangle^*\,,\ \) which means that an inner product of a vector with itself is a real number. Because of this, it makes sense to introduce an additional condition 4., which requires that \(\ \langle x,x\rangle\geq 0.\)

• The conditions 2. and \(\,\) 3. state in turn additivity and homogeneity of an inner product with respect to the second vector.

• The condition 4. imposes that an inner product of a vector with itself is a non-negative number, and the only vector for which it is zero is the zero vector.

The definition directly implies further properties of an inner product:

\[ \begin{align}\begin{aligned}\langle x_1+x_2,y\rangle\,=\,\langle y,x_1+x_2\rangle^*=\, [\,\langle y,x_1\rangle+\langle y,x_2\rangle\,]^*=\, \langle y,x_1\rangle^*+\,\langle y,x_2\rangle^*=\,\langle x_1,y\rangle\,+\,\langle x_2,y\rangle\,;\\\langle\alpha\,x,y\rangle\,=\,\langle y,\alpha\,x\rangle^*=\,[\,\alpha\,\langle y,x\rangle\,]^*= \,\alpha^*\langle y,x\rangle^*=\,\alpha^*\langle x,y\rangle\,.\end{aligned}\end{align} \]

Hence, an inner product is linear with respect to the second vector and antilinear with respect to the first one:

\[ \begin{align}\begin{aligned}\langle\,x,\ \alpha_1\,y_1\,+\,\alpha_2\,y_2\,\rangle\ =\ \alpha_1\ \langle x,y_1\rangle\,+\,\alpha_2\ \langle x,y_2\rangle\,,\\\langle\,\alpha_1\,x_1\,+\,\alpha_2\,x_2,\,y\,\rangle\ =\ \alpha_1^*\ \langle x_1,y\rangle\,+\,\alpha_2^*\,\langle x_2,y\rangle\,,\end{aligned}\end{align} \]

where \(\ \,\alpha_1,\alpha_2\in C,\ \ x,\,x_1,x_2,\ y,\,y_1,y_2\in V\,.\)

The definition of an inner product which is given in mathematical textbooks may differ from the one given here in point 3., which tends to be written as: \(\,(\alpha\,x,y)=\alpha\,(x,y)\,,\ \ \alpha\in C.\ \) Then an inner product is linear with respect to the first vector and antilinear with respect to the second one. For applications in physics, and especially in quantum mechanics, more suitable is the definition taken in this script.

One can easily prove the following

Theorem 0.

If one of the two vectors is zero, then the inner product vanishes:

(1)\[(\,x=\theta\quad\lor\quad y=\theta\,)\qquad\Rightarrow\qquad \langle x,y\rangle\,=\,0\,.\]

Indeed, \(\,\) if for example \(\ y=\theta,\ \) then \(\ y=0\cdot y\ \) and \(\ \,\langle x,y\rangle=\langle x,\,0\cdot y\rangle=0\cdot\langle x,y\rangle\,=\,0.\)

Remark:

The converse of the theorem (1) is not true: an inner product of two non-zero vectors may be zero (then we talk about orthogonal vectors).

An inner product defined on a real vector space \(\,V(R)\ \) is a map \(\,f:\ V\times V\rightarrow R\,,\ \) satisfying the conditions 1.- 4. The postulate 1. becomes then a symmetry condition: \(\ \langle y,x\rangle=\langle x,y\rangle,\ \ x,y\in V,\ \) and thus an inner product is linear with respect to both variables (it may be then defined as a real positive definite symmetric bilinear functional).

Definition.

A unitary space \(\,\) is a complex vector space with an inner product.

A real vector space with an inner product is called a \(\,\) Euclidean space.

Examples.

1.) A standard unitary space is a space of column vectors

\[\begin{split}C^n\ =\ \,\left\{\ \left[\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \dots \\ \alpha_n \end{array}\right]\,:\ \ \alpha_1,\,\alpha_2,\,\dots,\,\alpha_n\in C\ \right\}\,,\end{split}\]

where an inner product of vectors \(\quad \boldsymbol{x}\,=\, \left[\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \dots \\ \alpha_n \end{array}\right]\,,\quad \boldsymbol{y}\,=\, \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \dots \\ \beta_n \end{array}\right]\quad\) is given by a formula

\[\begin{split}\langle\boldsymbol{x},\boldsymbol{y}\rangle\,=\,\sum_{i\,=\,1}^n\ \alpha_i^*\,\beta_i \,=\;\alpha_1^*\,\beta_1\,+\;\alpha_2^*\,\beta_2\,+\;\dots\;+\;\alpha_n^*\,\beta_n \,=\;[\,\alpha_1^*,\,\alpha_2^*,\,\dots,\,\alpha_n^*\,]\ \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \dots \\ \beta_n \end{array}\right]\,.\end{split}\]

For example, if \(\ \ \boldsymbol{x}\,=\, \left[\begin{array}{c} 1+i \\ -2 \\ 4\,i \end{array}\right]\,,\ \ \boldsymbol{y}\,=\, \left[\begin{array}{c} -i \\ -1+2\,i \\ 0 \end{array}\right]\ \in\ C^3\quad\) then

\[\langle\boldsymbol{x},\boldsymbol{y}\rangle\ =\ (1-i)\,(-i)\,+\,(-2)\,(-1+2\,i)\,+\,(-4\,i)\,0\ =\ -i-1+2-4\,i\ =\ 1-5\,i\,.\]

2.) An example of a Euclidean space is a set of column vectors

\[\begin{split}R^n\ =\ \,\left\{\ \left[\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \dots \\ \alpha_n \end{array}\right]\,:\ \ \alpha_1,\,\alpha_2,\,\dots,\,\alpha_n\in R\ \right\}\,,\end{split}\]

where an inner product of vectors \(\quad \boldsymbol{x}\,=\, \left[\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \dots \\ \alpha_n \end{array}\right]\,,\quad \boldsymbol{y}\,=\, \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \dots \\ \beta_n \end{array}\right]\quad\) is given by a formula

\[\begin{split}\langle\boldsymbol{x},\boldsymbol{y}\rangle\,=\,\sum_{i\,=\,1}^n\ \alpha_i\,\beta_i \,=\;\alpha_1\,\beta_1\,+\;\alpha_2\,\beta_2\,+\;\dots\;+\;\alpha_n\,\beta_n \,=\;[\,\alpha_1,\,\alpha_2,\,\dots,\,\alpha_n\,]\ \left[\begin{array}{c} \beta_1 \\ \beta_2 \\ \dots \\ \beta_n \end{array}\right]\,.\end{split}\]

3.) A special application in quantum mechanics finds a unitary space \(\,L^2\ \) consisting of complex functions defined on a real line which are square integrable:

\[L^2\ \,=\ \,\left\{\ \varphi : R\rightarrow C\ \ :\ \ \int_{-\infty}^{+\infty}\ |\,\varphi(x)\,|^2\,<\,\infty\ \right\}\,,\]

where an inner product of \(\quad\varphi,\,\psi\in L^2\quad\) is given by \(\quad \langle\varphi,\psi\rangle\ =\ \displaystyle\int_{-\infty}^{+\infty}\ [\,\varphi(x)\,]^*\,\psi(x)\ dx\,.\)

4.) An example of a Euclidean space is a (2- or 3-dimensional) vector space of geometric vectors with an inner product given by \(\ \ \vec{a}\cdot\vec{b}\,=\,|\vec{a}|\,|\vec{b}|\,\cos\phi\,, \ \) where \(\,\phi=\angle(\vec{a},\vec{b})\,.\)

In a Euclidean space of 2-dimensional geometric vectors an inner product of a vector \(\vec{v}\) and a unit vector \(\vec{a}\) represents the scalar projection of \(\vec{v}\) onto \(\vec{a}\), that is, it is equal to the length of the segment \(AB\):

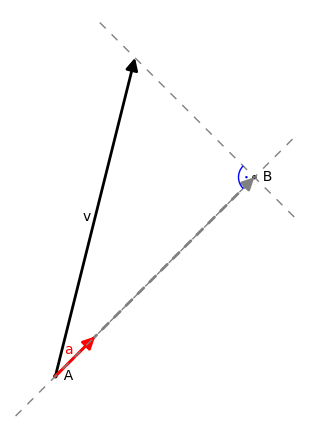
Furthermore, the vector \(\ \vec{AB}:=\ (\vec{v}\cdot\vec{a} )\,\vec{a}\ \) is the vector projection of \(\vec{v}\) onto \(\vec{a}\). If \(\vec{a}\) is not the unit vector, then the scalar projection and the vector projection of \(\vec{v}\) onto \(\vec{a}\) are given respectively by \(\ \vec{v}\cdot\frac{\vec{a}}{|\vec{a}|}\ \) and \(\ \frac{(\vec{v}\cdot\vec{a} )\,\vec{a}}{|\vec{a}|^2}\ \).

Having in mind applications, we wil mainly consider unitary (and so: complex) vector spaces. However, the introduced notions, properties and theorems are in general (with some exceptions) also true in Euclidean spaces.

The Schwarz Inequality

Theorem 1. \(\,\) (Schwarz inequality)

For any vectors \(\,x,y\ \) belonging to a unitary vector space \(\,V(C):\)

(2)\[|\,\langle x,y\rangle\,|^2\ \ \leq\ \ \langle x,x\rangle\,\langle y,y\rangle\,,\qquad x,y\in V(C)\,.\]

Proof. \(\,\) If \(\,y=\theta,\ \,\) the inequality (2) reads: \(\,0\,\leq 0\,.\)

We may assume then that \(\ \,y\neq\theta\,.\ \,\) Then, \(\,\) for any \(\,\alpha\in C:\)

\[ \begin{align}\begin{aligned}\langle\,x-\alpha\,y,\;x-\alpha\,y\,\rangle\ \ \geq\ \ 0\,,\\\langle x,x\rangle\ -\ \langle x,\,\alpha\,y\rangle\ -\ \langle\alpha\,y,\,x\rangle\ +\ \langle\alpha\,y,\,\alpha\,y\rangle\ \ \geq\ \ 0\,,\\\langle x,x\rangle\ -\ \alpha\,\langle x,y\rangle\ -\ \alpha^*\,\langle x,y\rangle^*\ +\ \alpha^*\alpha\ \langle y,y\rangle\ \ \geq\ \ 0\,.\end{aligned}\end{align} \]

In particular, we may substitute \(\ \ \alpha\ =\ \displaystyle\frac{\langle x,y\rangle^*}{\langle y,y\rangle}\,:\)

\[\langle x,x\rangle\ -\ \frac{\langle x,y\rangle^*}{\langle y,y\rangle}\ \langle x,y\rangle\ -\ \frac{\langle x,y\rangle}{\langle y,y\rangle}\ \langle x,y\rangle^*\ +\ \, \frac{\langle x,y\rangle}{\langle y,y\rangle}\ \frac{\langle x,y\rangle^*}{\langle y,y\rangle}\ \langle y,y\rangle\ \ \geq\ \ 0\,.\]

If we multilpy both sides of the inequality by \(\ \;\langle y,y\rangle>0,\ \;\) we obtain

\[ \begin{align}\begin{aligned}\langle x,x\rangle\,\langle y,y\rangle\ -\ |\,\langle x,y\rangle\,|^2\ -\ |\,\langle x,y\rangle\,|^2\ +\ \,|\,\langle x,y\rangle\,|^2\ \ \geq\ \ 0\,,\\\langle x,x\rangle\,\langle y,y\rangle\ \ \geq\ \ |\,\langle x,y\rangle\,|^2\,.\end{aligned}\end{align} \]

One can prove that the inequality (2) turns into equality if and only if vectors \(\,x,y\ \) are linearly independent. In a Euclidean space the inequality is of the form:

(3)\[\langle x,y\rangle^2\ \ \leq\ \ \langle x,x\rangle\,\langle y,y\rangle\,,\qquad x,y\in V(R)\,.\]

Examples.

1.) Schwarz Inequality applied to the space \(\,C^n\ \) states that \(\\\) for any two complex sequences \(\ \,(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_n)\,,\ \ (\beta_1,\,\beta_2,\,\dots,\,\beta_n) :\)

\[\left|\ \ \sum_{i\,=\,1}^n\ \alpha_i^*\ \beta_i\ \,\right|^{\ 2} \ \ \,\leq\quad \left(\ \sum_{i\,=\,1}^n\ |\,\alpha_i|^2\,\right)\ \left(\ \sum_{i\,=\,1}^n\ |\,\beta_i\,|^2\,\right)\,.\]

2.) In a Euclidean space \(\,R^n,\ \) for any two real sequences \(\ \,(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_n)\,,\ \ (\beta_1,\,\beta_2,\,\dots,\,\beta_n),\ \) the inequality (3) implies:

\[\left(\ \ \sum_{i\,=\,1}^n\ \alpha_i\ \beta_i\ \right)^2 \ \ \,\leq\quad \left(\ \sum_{i\,=\,1}^n\ \alpha_i^2\,\right)\ \left(\ \sum_{i\,=\,1}^n\ \beta_i^2\,\right)\,,\]

3.) In a unitary space \(\,L^2\ \) of square-inegrable functions, any functions \(\,\varphi,\psi\ \) satisfy the inequality

\[\left|\ \ \int_{-\infty}^{+\infty}\ [\,\varphi(x)\,]^*\,\psi(x)\ dx\ \ \right|^{\,2} \ \ \ \leq\ \ \ \int_{-\infty}^{+\infty}\ |\,\varphi(x)\,|^2\ dx\ \ \cdot\ \int_{-\infty}^{+\infty}\ |\,\psi(x)\,|^2\ dx\,.\]

4.) In a Euclidean space of geometric vectors with an inner product

\[\vec{a}\cdot\vec{b}\,=\,|\vec{a}|\,|\vec{b}|\,\cos\phi\,,\]

Schwarz Inequality gives: \(\quad (\vec{a}\cdot\vec{b})^2\ \,\leq\ \,|\vec{a}|^2\ |\vec{b}|^2\,, \quad\text{that is}\quad |\,\vec{a}\cdot\vec{b}\,|\ \,\leq\ \,|\vec{a}|\ |\vec{b}|\,.\)

This condition though is quite obvious, \(\,\) because \(\ \,|\cos\phi\,|\,\leq\,1\,.\)