Exercises

The exercises can be downloaded in a form of a notebook from here .

Exercise 1. 1

Consider a web consisting of 4 pages illustrated by the following graph:

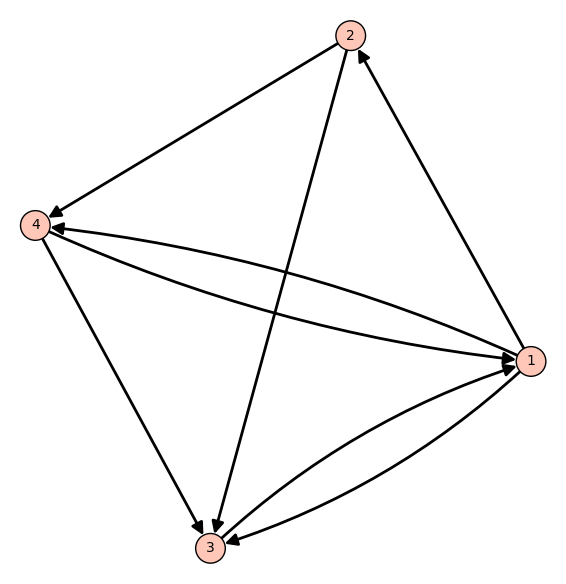
where an arrow from page A to page B indicates a link from page A to page B.

1. Write down link matrix for this web and compute an importance score vector of this web using basic approach presented in Example 1., Google’s Application - PageRank Algorithm. You can make the computations in the window below.

To verify whether the adjacency matrix \(A\) you use is correct, at the end of your code write

sage: W=DiGraph(A)
sage: W.relabel({0:'1' , 1:'2', 2:'3', 3:'4'})
sage: W.plot()

and check whether the resulting graph is the same as above.

2. Compute an importance score vector of this web using formula (1). Later compare the result with the importance score vector from point 1.

3. Suppose the people who own page 3 are infuriated by the fact that its importance score, computed using formula (1), is lower than the score of page 1. In an attempt to boost page 3’s score, they create a page 5 that links to page 3; page 3 also links to page 5. Does this boost page 3’s score above that of page 1?

First plot the graph presenting the new situation.

Now compute the new ranking using formula (1).

Exercise 2. 1

Consider again the web from previous exercise with the addition of a page 5 that links to page 3, where page 3 also links to page 5:

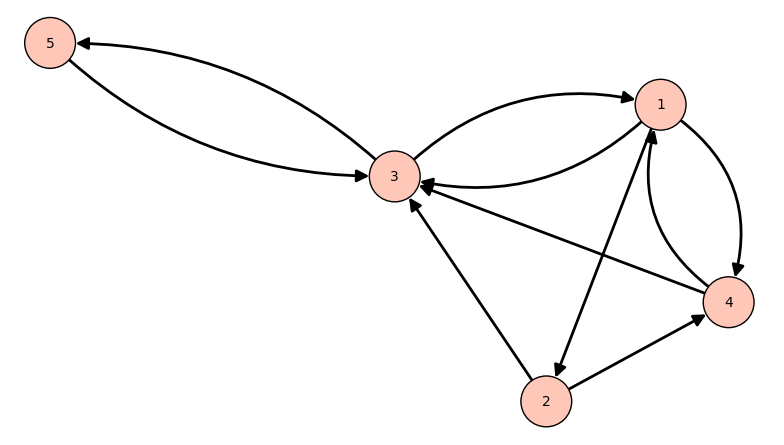
1. Calculate the new ranking by finding the eigenvector of matrix \(M\) defined by equation (2). Use \(\ m=0.15\ \).

2. Add a sixth page that links to every page of the web in the previous exercise, but to which no other page links. Write the code to plot the new web in the window below.

Now rank the pages using

a). the formula (1),

b). the matrix \(M\) defined by equation (2) with \(\ m=0.15\ \).

Compare the results.

3. Use the power method to compute the ranking of the web from point 2. Take different initial vectors \(\ x_0\ \) and see how many iterations you need to obtain the result which is close to the result from 2b). See also what happens if some entries of \(\ x_0\ \) are not positive or do not sum up to one. How does the value of \(m\) influence the result?

Exercise 3. (dangling nodes)

Consider the web illustrated by the following graph:

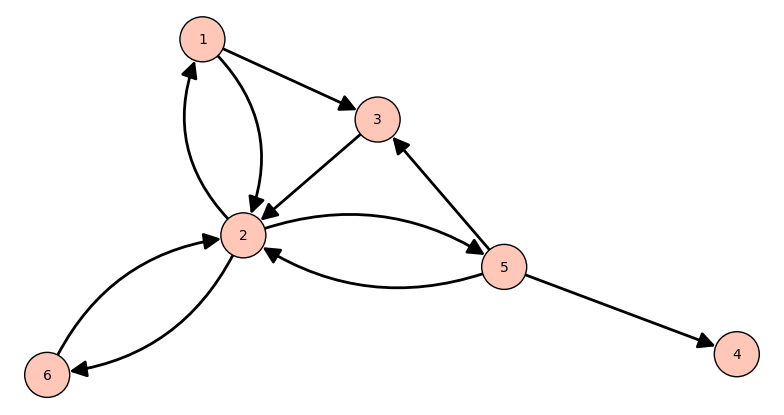
Compute ranking of the pages by finding the Perron eigenvector.

Exercise 4. (webs randomly generated)

The code below returns a random web with \(\ n\ \) pages (more precisely: a random directed graph on \(\ n\ \) nodes), where the probability of a link from one page to another is \(\ p\ \). Check how the result changes if you vary value of \(\ p\ \) between \(0\) and \(1\).

1. Find the link matrix for this web.

2. Compute ranking of this web using different methods.

Exercise 5. (disconnected webs)

Consider a web consisting of two (disconnected) subwebs:

Rank the pages using the matrix M defined by equation (2) with \(\ m=0.15\ \). See what happens if you change the value of \(m\). Do the same with a web consisting of more subwebs.

1(1,2)

This exercise was taken from an article of K. Bryan and T. Leise, “The $25,000,000,000 Eigenvector. The Linear Algebra Behind Google”. Available at https://www.rose-hulman.edu/~bryan/google.html .