Google’s Application - PageRank Algorithm¶
A big part of Google’s success is its PageRank Algorithm which rates importance of the websites and then presents them accordingly to the user. Quite often most relevant and helpful pages are listed first. It turns out that the reason is yet another disguise of the eigenvector problem. This section is based on an article of Bryan and Leise “The $25,000,000,000 Eigenvector. The Linear Algebra Behind Google” [BL], which is available at https://www.rose-hulman.edu/~bryan/google.html .
One of the tasks of Google browser is to locate the websites with public access and index them with relevant keywords and phrases. Once this is done, the websites have to be ordered according to their importance. The main idea behind this procedure relies on an assumption that more important web pages are linked by other pages more often. We will call the links to a given page by the backlinks.
Example 1.
Consider a web consisting of four pages which are linked with each other according to the following scheme (an arrow from page A to page B indicates a link from page A to page B):
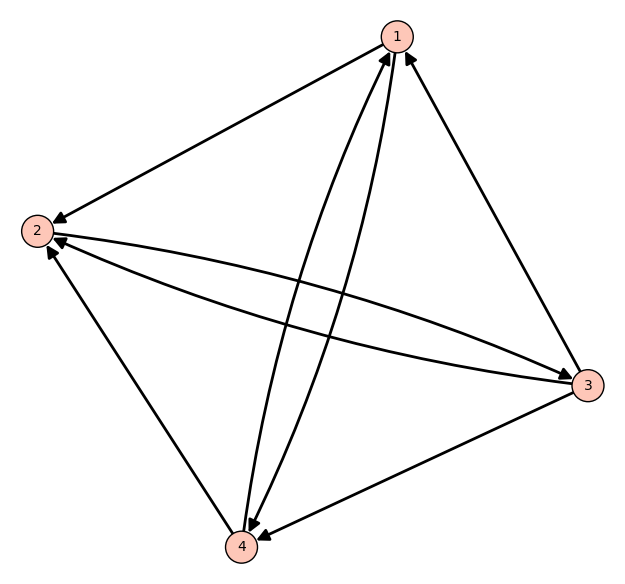
It was plotted using the following code:
sage: A = matrix([[0,1,0,1], [0,0,1,0],[1,1,0,1],[1,1,0,0]])
sage: W=DiGraph(A)
sage: W.relabel({0:'1' , 1:'2', 2:'3', 3:'4'})
sage: W.plot()
where the matrix \(A\) determines the arrows between the websites, e.g. the first row of the matrix contains \(1\) at the entries 2 and 4 because website 1 links to these pages. In other words: the \(i\)-th row tells us to which pages page \(i\) links, and the \(i\)-th column tells us where the backlinks for page \(i\) come from. Such a matrix is called an adjacency matrix. Note that we had to relabel the names of vertices in the graph, so that the enumeration starts from 1 and not from 0.
Having created the web by such a code, we can easily count the number of backlinks of a given page - it suffices to add the entries in a corresponding column:
sage: n=A.ncols() # size of the (square) matrix A
sage: b=vector(0 for i in range(n))
sage: for i in range(n):
sage: b[i]=sum(A[j][i] for j in range(n))
sage: print b
(2, 3, 1, 2)
The outcome suggests that the page 2 is most important, next are the pages 1 and 4 of equal importance, and the least important is the page 3. One may view this as a result of democrative vote of websites for the most important one.
The basic approach presented in the above example does not take into account a few important factors:
a link from an important page should matter much more than a link from a mediocre page;
not all the websites are connected with each other via links, in fact the actual web comprises a highly disconnected graph; how to compare such pages?
is there always a unique most important website?
some pages do not contain any links (such pages are called dangling nodes).
In what follows we extend the idea presented above to tackle all these problems.
Problem 1.
It should matter where the backlinks come from.
Denote by \(\ x_i\ \) the importance score of the web page \(\ i\ \) (we do not specify yet how it may be computed), and let \(\ n_i\ \) be the number of links on the page \(\ i\,.\) For instance, in the example presented above, the score of page 1 would be determined by the relation \(\ x_1=x_3+x_4\,.\) However, in this way the page 3 may vote three times. To avoid such a situation, we normalise the vote by the the number of links that the page contains, i.e. the score of page 1 should be rather given by a formula \(\ x_1=\frac{x_3}{3} +\frac{x_4}{2}\,.\) In general, if a web consists of \(\ n\ \) pages and \(\ L_k\subset\{ 1,2,\ldots ,n\}\ \) denotes the set of pages which link to the page \(\ k\,,\ \) then we define (assumming that \(\ L_k\neq\emptyset\) ):
We will assume additionally that a link from a page to itself does not count.
Example 2.
Consider the web from Example 1. The importance scores of the websites are as follows:
The above equalities may be written in a form of matrix equation \(\ x=Ax\,,\ \) where
In this way, finding importance scores of web pages is equivalent to finding an eigenvector of the matrix \(\ A\ \) with the eigenvalue \(1\,\)! Let us check first whether \(1\) is indeed an eigenvalue of \(\ A\,.\ \) We will do the computations in Sage.
sage: Ad = matrix([[0,1,0,1], [0,0,1,0],[1,1,0,1],[1,1,0,0]])
sage: W=DiGraph(A)
sage: # First we need to normalise adjacency matrix Ad so that the sum of entries in each row is 1.
sage: n=Ad.ncolumns() # counts the number of columns of Ad
sage: l=vector(0 for i in range(n))
sage: for i in range(n):
sage: l[i]=sum(A[i,j] for j in range(n)) # counts the number of links on page i
sage: D=matrix(n) # n by n zero matrix
sage: for i in range(n):
sage: D[i,i]=l[i]
sage: print D.inverse()*Ad
[ 0 1/2 0 1/2 ]
[ 0 0 1 0 ]
[1/3 1/3 0 1/3 ]
[1/2 1/2 0 0 ]
# Now note that the matrix we are looking for is the transpose of the normalised adjacency matrix.
sage: A=(D.inverse()*Ad).transpose()
sage: print A
[ 0 0 1/3 1/2 ]
[1/2 0 1/3 1/2 ]
[ 0 1 0 0 ]
[1/2 0 1/3 0 ]
We are ready to compute the eigenvalues of \(A\). This can be done in a few ways: by computing and factorising the characteristic polynomial
sage: f=A.charpoly()
sage: f.factor()
(x - 1) * (x + 1/2) * (x^2 + 1/2*x + 1/6)
by applying a direct function
sage: A.eigenvalues()
[1, -1/2, -0.25000000000000000? - 0.3227486121839514?*I, -0.25000000000000000? + 0.3227486121839514?*I]
or even by asking sage to provide directly the eigenvectors
sage: A.eigenvectors_right()
[(1, [
(1, 3/2, 3/2, 1)
], 1), (-1/2, [
(1, 0, 0, -1)
], 1), (-0.25000000000000000? - 0.3227486121839514?*I,
[(1, 0.25000000000000000? + 0.9682458365518542?*I, -2.2500000000000000? - 0.9682458365518542?*I, 1)],
1), (-0.25000000000000000? + 0.3227486121839514?*I,
[(1, 0.25000000000000000? - 0.9682458365518542?*I, -2.2500000000000000? + 0.9682458365518542?*I, 1)],
1)]
Note that the function eigenvectors_right() provides first an eigenvalue, and then the associated eigenvector.
We obtained a completely different importance score vector!
Basic approach: \(\ (2, 3, 1, 2)\ \).
Normalised approach: \(\ (1, \frac32, \frac32, 1)\ \).
However, if we look once again at the picture presenting our web, we see that the new result is not that surprising after all: page 2 gets most votes, and page 3 just one, but this one vote comes from page 2 which is considered to be most important.
Every matrix which arises in the same way as the matrix \(A\) in the above example will be called a link matrix. Note that all the entries of a link matrix are nonnegative and, thanks to the normalisation, the entries in each column sum to one, that is, a link matrix is an example of a column-stochastic matrix.
The problem of existence of an eigenvector with the eigenvalue \(1\) solves the following proposition (proven in [BL]).
Proposition.
Every column-stochastic matrix has \(1\) as an eigenvalue.
We denote by \(\ V_1(A)\ \) the eigenspace for eigenvalue \(1\) of a column-stochastic matrix \(A.\) If \(A\) is the link matrix, the space \(\ V_1(A)\ \) contains vectors which carry information about importance scores of websites. However, is \(\ V_1(A)\ \) always \(1\)-dimensional?
Example 3.
Consider a web consisting of two disconnected subwebs \(\ W_1\ \) (pages 1-4) and \(\ W_2\ \) (pages 5,6):
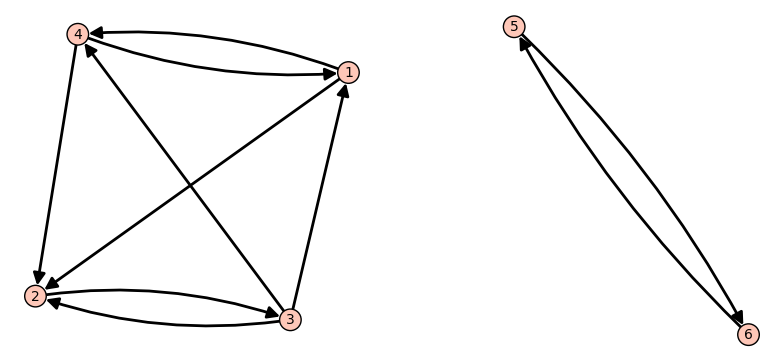
The diagram was made by adding two paths to a graph from Example 1.:
sage: W.add_path(['5','6'])
sage: W.add_path(['6','5'])
sage: W.plot()
Note that if we apply the function W.add_path() then new vertices are created automatically. (We wrote W.add_path(['5','6']) instead of W.add_path([5,6]) so that if we call a function W.vertices(), then we obtain a vector [‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’] rather than [5, 6, ‘1’, ‘2’, ‘3’, ‘4’].)
Following an approach presented in Example 2. we obtain exactly the same relations for \(\ x_1, x_2, x_3, x_4\ \), and additionally \(\ x_5= \frac{x_6}{1} =x_6\,.\) This leads into the matrix equation \(\ x=Ax\ \) with
As before, we compute the eigenvectors for the eigenvalue \(1\) using Sage (now we know that there exists at least one such eigenvector):
# First, we find an adjacency matrix of the web W.
sage: Ad=W.adjacency_matrix()
sage: print Ad
[0 1 0 1 0 0]
[0 0 1 0 0 0]
[1 1 0 1 0 0]
[1 1 0 0 0 0]
[0 0 0 0 0 1]
[0 0 0 0 1 0]
# Secondly, we find the link matrix.
sage: n=Ad.ncols() # counts the number of columns of Ad
sage: l=vector(0 for i in range(n))
sage: for i in range(n):
sage: l[i]=sum(A[i,j] for j in range(n)) # counts the number of links on page i
sage: D=matrix(n) # n by n zero matrix
sage: for i in range(n):
sage: D[i,i]=l[i]
sage: A=(D.inverse()*Ad).transpose()
sage: print A
[ 0 0 1/3 1/2 0 0]
[1/2 0 1/3 1/2 0 0]
[ 0 1 0 0 0 0]
[1/2 0 1/3 0 0 0]
[ 0 0 0 0 0 1]
[ 0 0 0 0 1 0]
# Finally, we compute the eigenvectors. This time we do it differently.
sage: B=A-identity_matrix(n)
sage: B.rref() # B in the reduced row echelon form
[ 1 0 0 -1 0 0]
[ 0 1 0 -3/2 0 0]
[ 0 0 1 -3/2 0 0]
[ 0 0 0 0 1 -1]
[ 0 0 0 0 0 0]
[ 0 0 0 0 0 0]
Hence,
and thus
This time the space of eigenvectors is \(\ 2\)-dimensional and \(\,\) any \(\,\) of the vectors
could carry information about an importance score of the websites.
In fact, if a web \(\ W\ \) contains \(r\) subwebs, then \(\ \mathrm{dim}(V_1(A))\geq r\,.\) Indeed, if \(\ W_1,W_2\ldots W_r\ \) are subwebs of \(\ W\ \) and \(\ A_1, A_2,\ldots, A_r\ \) are their link matrices, then the link matrix \(\ A\ \) of \(\ W\ \) is of the form
and
where \(\ v_1, v_2 \ldots, v_r\ \) are eigenvectors for the eigenvalue \(1\) of matrices \(\ A_1, A_2,\ldots, A_r\,.\)
Problem 2.
How to compare web pages that are not connected via a path of links and find the most important one?
To deal with this problem we will assume for simplicity that every page has at least one link.
Assume that a web \(\ W\ \) consists of \(\ n\ \) pages. Let \(\ S\ \) be an \(\ n\times n\ \) matrix with all entries equal to \(\ \frac1n\,\). We replace the link matrix \(\ A\ \) with the matrix
where \(\ m\in [0,1]\ \) is a certain fixed value. The value of \(m\) originally used by Google was \(0.15\). It is not difficult to check that the matrix \(M\) is a column-stochastic matrix, and thus it has an eigenvector for the eigenvalue \(1 .\,\) Moreover, one can prove (c.f. [BL])
Proposition.
If \(M\) is column-stochastic and each of its entry is positive, then \(\ \mathrm{dim}(V_1(M))=1\,.\)
Example 4.
Consider a web from Example 3. and take \(\ m=0.15\,.\) Then the matrix \(M\) may be easily found by the following code:
sage: A=matrix(QQ,[[0, 0, 1/3, 1/2, 0, 0], [1/2, 0, 1/3, 1/2, 0, 0], [0, 1, 0, 0, 0, 0], [1/2, 0, 1/3, 0, 0, 0],
[0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 0]])
sage: n=A.ncols()
sage: m=0.15
sage: S=ones_matrix(QQ,n)/n # the all ones matrix multiplied by 1/n
sage: M = (1−m)*A + m*S
sage: print M.n(digits=3) # each entry has a precision up to 0.001
[0.0250 0.0250 0.308 0.450 0.0250 0.0250]
[ 0.450 0.0250 0.308 0.450 0.0250 0.0250]
[0.0250 0.875 0.0250 0.0250 0.0250 0.0250]
[ 0.450 0.0250 0.308 0.0250 0.0250 0.0250]
[0.0250 0.0250 0.0250 0.0250 0.0250 0.875]
[0.0250 0.0250 0.0250 0.0250 0.875 0.0250]
We can easily in SageMath determine the eigenvector corresponding to eigenvalue 1.
Note
It is important to change ring of the matrix \(M\) to RDF or CDF, since the computations might cause problems in exact arithmetics.
Experiment with Sage!
Run the code below to compute the eigenvector for eigenvalue 1.
we see that the most important website is the second one, and just after it is the third one, which agrees to some extent with both normalised and basic approach.
Thanks to Sage we did not have to spend a lot of time doing unpleasant computations by hand. However, the bigger the matrix is, the longer one has to wait for the answer. And if currently there are almost \(\ 2\cdot 10^9\ \) websites 2…
Problem 3.
How to compute an eigenvector of a huge matrix efficiently?
We will discuss, after [BL], an idea behind \(\,\) the power method . \(\,\) This method bases on
Theorem [BL].
The matrix \(M\) defined by equation (2) for a web with no dangling nodes will always be a column-stochastic matrix with positive entries and so have a unique vector \(\ q=[q_i]_n\ \) with positive components such that \(\ Mq = q\ \) and \(\ \sum_{i=1}^n q_i=1\ \). The vector \(\ q\ \) may be computed as the limit of iterations
where \(\ x_0=[x_{0,i}]_n\ \) is any initial vector with positive components such that \(\ \sum_{i=1}^n x_{0,i}=1\ \), and \(\ s=[1/n,\ldots, 1/n]^T\ \).
This theorem does not only tell us that every column-stochastic matrix has a \(\,\) unique \(\,\) eiegenvector for the eigenvalue \(1\) (which results in a unique importance score ranking), \(\,\) but also \(\,\) how \(\,\) it may be computed. And this computation is surprisingly simple! Note also that if we apply the matrix \(\ M\ \) to a vector \(\ x=[x_i]_n\ \) whose entries sum up to one: \(\ \sum_{i=1}^n x_i=1\ \), then
because
This fact significantly decreases the amount of computations that have to be performed. Indeed, to calculate \(\ Mx\ \) it suffices to add the known quantity \(\ ms\ \) to a product \(\ (1−m)Ax\ \), where the matrix \(A\) consists mainly of zeros.
Example 5.
We will compare the results from Example 4. with a construction suggested by the above theorem. The code below takes as the initial vector \(\ x_0=[1/n,\ldots, 1/n]\ \) , where \(n\) is the size of matrix \(A\), and performs \(10\) iterations. See what happens if you change the entries of \(x_0\), number of iterations or the value of \(m\). How good is the approximation of the importance score vector? How many iterations need to be done to obtain the same ranking of web pages as in Example 4.? See also what happens if some entries of \(x_0\) are non-positive or do not sum up to one.
Problem 4.
If a web contains dangling nodes, then the link matrix is not column-stochastic and thus the methods discussed above cannot be applied.
If a web contains websites with no links (i.e. dangling nodes), then the corresponding columns of the link matrix \(A\) will contain only zeros. In such situation \(A\) is column-substochastic, that is, sum of entries of \(A\) is less or equal to one. The eigenvalues of \(A\) still need to be less or equal to one, but \(1\) does not have to be an eigenvalue. However, \(A\) will still have a positive eigenvalue and a corresponding eigenevctor with non-negative entries may be taken as the importance score vector. If instead of a link matrix \(A\) we consider the matrix \(M\) defined by the formula (2), then the eigenvector will be unique:
Perron’s theorem.
Let \(\ A\ \) be a square matrix with positive entries and \(\ \lambda\ \) its greatest eigenvalue. Then:
\(\ \lambda > 0\ \),
algebraic multiplicity of \(\ \lambda\ \) is equal to one,
there exists a unique eigenvector for \(\ \lambda\ \) with all the entries positive (the Perron vector),
entries of eigenvectors for other eigenvalues are not all positive.
More general situation of a matrix with non-negative entries is treated in Perron–Frobenius Theorem, which we do not include here.
Example 6.
Consider the web illustrated by the following graph:
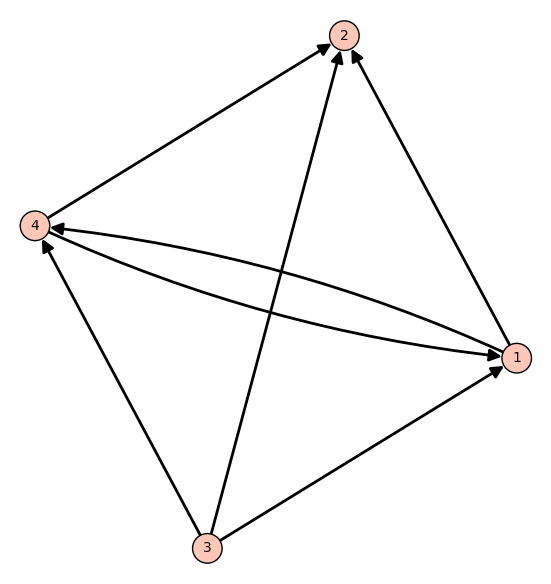
Its link matrix is
We will compute an eigenvector of \(A\) for the greatest eigenvalue using the formula (1) without constructing the matrix \(M\):
sage: A=matrix(QQ,[[0, 0, 1/3, 1/2], [1/2, 0, 1/3, 1/2], [0, 0, 0, 0], [1/2, 0, 1/3, 0]])
sage: l=sorted(A.eigenvectors_right()) # sorted list of eigenvectors
sage: print l, '\n'; l[len(l)-1] # len(l) = length of the list l
[(-1/2, [
(1, 0, 0, -1)
], 1), (0, [
(0, 1, 0, 0)
], 2), (1/2, [
(1, 2, 0, 1)
], 1)]
(1/2, [
(1, 2, 0, 1)
], 1)
