Reakcje Biełusowa-Żabotyńskiego¶
Wstęp: opis reakcji¶
Istnieje wiele przykładów reakcji Biełousowa-Żabotyńskiego (będziemy czasami używali skrótu B-Ż). Są one niezwykłe i mają niezwykłą historię. Dlaczego? Ponieważ są to reakcje oscylacyjne. W 1951 roku Biełousow opisał taką reakcję i napisał pracę na ten temat. Edytorzy czasopisma, do którego został wysłany maszynopis pracy, nie zaakceptowali jej do druku, nie wierząc w jej wyniki. Sześć lat później, Biełousow znowu wysłał pracę do publikacji, ale tym razem do innego czasopisma. I znowu edytorzy byli sceptyczni. Zaproponowali aby przedstawić tylko opis reakcji, ale Bielousow nie zgodził się. Obrażony postanowił nie wysyłać więcej jej do publikacji. W 1961 roku inny adept radzieckiej nauki, Żabotyński odkrył odkrytą już reakcję, ale o tym nie wiedział. Na szczęście opiekun naukowy Żabotyńskiego znał wyniki prac Biełousowa i prosił swego podopiecznego o kontakt z Biełousowem. Niestety, w tamtych czasach nie było ani telefonii komórkowej, ani internetu. Dopiero w 1968 roku, w czasie obrad sympozjum w Pradze, świat zachodni dowiedział się o tych niezwykłych reakcjach.
Reakcje oscylacyjne występują np. w wodnym roztworze w temperaturze pokojowej, w której zachodzą okresowe zmiany barwy roztworu z okresem ok. jednej minuty. Na podstawowy mechanizm reakcji składa się utlenianie kwasu malanowego w środowisku kwaśnym przez jony bromianowe BrO 3 w obecności katalizatora - jonów ceru. Okresowe oscylacje obserwowane są w stężeniu jonów ceru. Oscylacje przejawiają się jako zmiany koloru przy przejściu Ce 3+ w Ce 4+ . Obecnie znanych jest wiele reakcji, które mogą zachowywać się okresowo. Mianem reakcji BŻ nazywa się klasę reakcji, w których związek organiczny jest utleniany przez jony bromianowe wspomagane jonami metalu w środowisku kwaśnym. Jeśli substraty dyfundują mogą się wówczas wytwarzać wzory przestrzenne. Dla katalizatorów będących jonami innych metali np. żelaza Fe 2+ i Fe 3+ zmiany barw mogą być bardziej spektakularne czerwony ↔ niebieski. Istnieją jeszcze inne reakcje tego typu. Np. reakcja Briggsa-Rauschera jest jeszcze atrakcyjniejsza, bo oscylacje są bardzo kontrastowe (bezbarwny-złoty-granatowy) i bardzo szybkie: co kilkanaście sekund; a jej uruchomienie jest bardzo proste. Reagenty: zakwaszony roztwór jodanu, kwasu malonowego, nadtlenku wodoru, katalizowany solą manganawą, z dodatkiem skrobi. Mechanizm tej reakcji jest słabo poznany; prawdopodobnie są to dwie sprzężone reakcje oscylacyjne.
W przykładowej reakcji miesza się trzy wyjściowe roztwory wodne, które zaraz po zmieszaniu dają barwę zieloną, która po chwili przechodzi w niebieską, purpurową, czerwoną aż do powrotu do zieleni. Roztworami tymi są:
0,23 M KBrO 3 (bromian(V) potasu)
0,31 M kwas malonowy (lub kwas cytrynowy) + 0,059 M KBr
0,019 M (NH 4) 2 Ce(NO 3) 6 + 2,7 M H 2 SO 4
Oprócz tego do układu reakcji dodaje się niewielką ilość ferroiny, która zmienia barwę w wyniku ubocznej reakcji redoks, lecz nie wpływa bezpośrednio na przebieg całego procesu.
W sprzyjających warunkach, przy bardzo dokładnym utrzymaniu proporcji i przy zachowaniu idealnej czystości cykl powtarza się kilkanaście razy. Po zmieszaniu zakwaszonego roztworu bromianu, kwasu malonowego, soli ceru oraz wskaźnika - ferroiny, przez pewien czas istnieje stan indukcji. Szczegółowy mechanizm reakcji jest bardzo zawiły. Obejmuje trzy grupy złożonych procesów, które skrótowo opiszemy poniżej.
W roztworze początkowo istnieje pewne stężenie jonów bromkowych, które pełnią kluczową rolę w całym mechanizmie. Jony bromkowe są powoli usuwane w wyniku utleniania bromianem:
2Br – + BrO 3 - + 3CH 2 (COOH) 2 + 3H + = 3CHBr(COOH) 2 + 3H 2 O
W wyniku reakcji A stężenie jonów bromkowych stopniowo maleje. Z chwilą, gdy spadnie ono poniżej pewnej dolnej wartości progowej, zachodzi raptowne utlenienie jonów cerawych do jonów cerowych:
4Ce 3+ + BrO 3 – + CH 2 (COOH) 2 + 5H + = 4Ce 4+ + CHBr(COOH) 2 + 3H 2 O
Jest to reakcja autokatalityczna, która jest skutecznie hamowana przez jony bromkowe. Aby mogła zajść, trzeba poczekać, aż stężenie jonów bromkowych spadnie poniżej pewnej dolnej wartości progowej. W wyniku autokatalizy jony ceru bardzo raptownie przechodzą w postać utlenioną; towarzyszy temu gwałtowna zmiana barwy wskaźnika na niebieski.
W kolejnej fazie powstały kwas bromomalonowy zostaje utleniany, uwalniane są aniony bromkowe, których stężenie rośnie w wyniku reakcji C szybciej, niż ich konsumpcja w reakcji A. Stężenie utlenionej postaci ceru maleje, a wskaźnik stopniowo zmienia barwę na różową.
4Ce 4+ + CHBr(COOH) 2 + 2H 2 O = Br – + 4Ce 3+ + HCOOH + 2CO 2 + 5H +
Po przekroczeniu pewnej górnej wartości progowej stężenia bromku, następuje ponowne zablokowanie autokatalitycznej reakcji B (autoinhibicja). Powstają duże ilości jonów bromkowych. Trzeba odczekać, aż zostaną one skonsumowane w reakcji A. Potem cykl zostaje kolejny raz odtworzony. Oscylacje zachodzą tylko do czasu osiągnięcia minimalnego granicznego odchylenia od stanu równowagi; dalszy przebieg ma charakter monotoniczny.
Sumarycznie reakcja ta sprowadza się do odwracalnego utlenienia kwasu malonowego do dwutlenku węgla przez jony bromianowe, zaś jony ceru pełnią w procesie rolę katalizatora:
3 CH 2 (COOH) 2 + 4 BrO 3 - → 4 Br - + 9 CO 2 + 6 H 2 O
W istocie jednak reakcja ta składa się z dwóch procesów zachodzących cyklicznie jeden po drugim.
Pierwszy proces (A) przebiega sumarycznie wg równania:
BrO 3 - + 5 Br - + 6 H + → 3 Br 2 + 3 H 2 O
i składa się z następujących reakcji elementarnych:
BrO 3 - + Br - + 2 H + → HBrO 2 + HOBr
HBrO 2 + Br - + H + → 2 HOBr
HOBr + Br - + H + → Br 2 + H 2 O
Powstający brom reaguje z kwasem malonowym wg równania:
Br 2 + CH 2 (COOH) 2 → BrCH(COOH) 2 + Br - + H +
Druga reakcja (B) przebiega sumarycznie następująco:
2 BrO 3 - + 12 H + + 10 Ce 3+ → Br 2 + 6 H 2 O + 10 Ce 4+
i składa się z następujących aktów elementarnych:
BrO 3 - + HBrO 2 + H + → 2 BrO 2 • + H 2 O
BrO 2 • + Ce 3+ + H + → HBrO 2 + Ce 4+
2 HBrO 2 → HOBr + BrO 3 - + H +
2 HOBr → HBrO 2 + Br - + H +
HOBr + Br - + H + → Br 2 + H 2 O
Kluczowy wpływ na zmianę barwy ma cykliczna zmiana stężenia jonów Ce 3+ i Ce 4+, które sumarycznie można przedstawić w formie następującego równania:
2 Ce 3+ + BrO 3 - + HBrO 2 + 3 H + → 2 Ce 4+ + H 2 O + 2 HBrO 2
4Ce 4+ + CHBr(COOH) 2 + 2H 2 O = Br – + 4Ce 3+ + HCOOH + 2CO 2 + 5H +
Powstające jony ceru Ce 4+ utleniają atomy żelaza(II) do żelaza(III). Jony Ce 3+ są bezbarwne, jony Ce 4+ posiadają intensywnie żółtą barwę. Kompleks ferroiny z atomami żelaza(II) ma barwę czerwoną, zaś z atomami żelaza(III) niebieską. Kombinacja żółtej barwy jonów Ce 4+ i niebieskiej kompleksu ferroiny z atomami żelaza(III) daje w efekcie barwę zieloną.
Cykliczne zmiany stężenia jonów Ce 3+ i Ce 4+ wynikają z następującej kombinacji zjawisk:
reakcja (B) ma charakter autokatalityczny - początkowo zatem przebiega bardzo powoli, aby w pewnym momencie nagle gwałtownie przyspieszyć
reakcja (A) zachodzi przy odpowiednio wysokim, granicznym stężeniu jonów bromianowych (BrO 3 -), które są generowanie w reakcji (B)
Stężenie początkowych roztworów jest tak dobrane, aby najpierw zaszła szybko reakcja (A), zanim reakcja (B) zdąży nabrać tempa i jednocześnie tak, aby reakcja (B) zdążyła się „rozpędzić”, zanim w układzie całkowicie nie zanikną jony bromkowe Br - i H +. W związku z tym, w układzie dominuje najpierw reakcja (A), która nie ma bezpośredniego wpływu na zmianę barwy, a następnie większą rolę zaczyna odgrywać reakcja (B), która jednak jednocześnie dostarcza substratu dla reakcji (A), co po pewnym czasie powoduje ponowne przyspieszenie (A) i spowolnienie (B).
Równania kinetyczne: oregonator¶
W literaturze opis reakcji B-Ż nie jest jednolity. Można pogubić się w tym, ile jest reakcji elementarnych, ile istotnych, ile pośrednich, itd. Opisane powyżej wszystkie reakcje chamiczne są trudne do modelowania matematycznego. Jednak praktyka i doświadczenie w modelowaniu pokazuje, że należy uwzględnić tylko najbardziej istotne elementy jakie pojawiają się w powyższych reakcjach. Innymi słowy, należy umiejętnie zredukować ilość reakcji i sformułować efektywne reakcje. Jeden z takich zredukowanych modeli został opracowany przez Fielda, Korosa i Noyesa (1974) z University of Oregon. Dlatego nazywa się „oregonatorem” lub mechanizmem FKN. Jest zbudowany z 5 elementarnych reakcji jakie pojawiają sie w reakcjach Biełousowa-Żabotyńskiego. Niech student/studentka (hm, nie jestem pewien: jeżeli minister/ministra to może student/studenta??) postara się je odszukać w powyższym gąszczu i porówna z poniżej zaprezentowanymi 5 reakcjami. Wprowadźmy oznaczenia dla odpowiednich stężeń:
X = [HBrO 2 ] , Y = [Br − ], Z = [Ce 4+], A= [BrO 3 − ], B = [CH 2 (COOH) 2 ], P = [HOBr] lub P=[BrCH(COOH) 2]
Koncentracje A, B oraz P nie zmieniają się (lub zmieniają sie bardzo wolno w porównaniu do zamian stężeń X, Y oraz Z. Efektywne reakcje to reakcje:
A+Y → X +P w tempie \(k_1\)
X + Y → 2P w tempie \(k_2\)
A + X → 2X + 2Z w tempie \(k_3\)
2X → A + P w tempie \(k_4\)
B + Z → u Y w tempie \(k_5\)
Symbol u w ostatniej reakcji to współczynnik stechiometryczny (liczba przypisana do określonego reagenta określająca proporcję w jakiej uczestniczy on w reakcji w stosunku do innych reagentów).
Uwaga: W prawie wszystkich źródłach (ksiązkach, pracach, in ternecie), używa się oznaczenia f na ten współczynnik. Ale my rezerwujemy f do tradycyjnego oznaczania funkcji.
Odpowiedznie równania kinetyczne są postaci:
Należy te równania przeskalować do nowych zmiennych
gdzie
Przeskalowane równania redukują się do postaci zwanej „oregonatorem”:
Ta postać równań jest powszechnie stosowana do opisu reakcji B-Ż. W równanich tych występują 4 parametry: \(c, q, \delta, u\). Rząd ich wielkości jest następujący:
Znalazłem też taki zestaw danych (patrz: http://www.rose-hulman.edu/search.aspx?q=bielousov):
Własności „oregonatora”¶
Reakcje opisywane za pomocą „oregonatora” posiadają bogactwo własności dynamicznych ponieważ „oregonator” to układ dynamiczny opisywany przez układ 3 równań różniczkowych zwyczajnych pierwszego rzędu. Jego tzw. przestrzeń fazowa to zbiór możliwych wartości \(\{x, y, z\}\), a wymiar tej przestrzeni oczywiście wynosi 3. Jak udowodnili nasi przyjaciele matematycy, jest to minimalny wymiar przestrzeni, aby układ mógł wykazywać własności chaotyczne. Dynamika takiego układu może w ogólności wykazywać następujące cechy:
istnienie stanów stacjonarnych
istnienie orbit periodycznych
istnienie orbit chaotycznych
istnienie dziwnych atraktorów
Okazuje się, że oryginalny „oregonator” przedstawiony tutaj, nie wykazuje własności chaotycznych. Oznacza to, że własności 3 oraz 4 nie można zaobserwować dla tego modelu. W 1992 roku, zaproponowano zmodyfikowany model reakcji B-Ż który wykazuje chaos. Szczegóły można znależć w oryginalnej pracy:
Gyorgyi and R. J. Field, (1992) A Three-Variable Model of Deterministic Chaos in the Belousov-Zhabotinsky Reaction. Nature, 355, 808-810.
Stany stacjonarne¶
Zbadajmy, czy istnieją stany stacjonarne i czy są one stabilne. Podobnie jak w analizie dynamiki populacyjnej, warunkiem na istnienie stanów stacjonarnych jest istnienie rozwiązań układu 3 równań algebraicznych otrzymanych jako prawe strony „oregonatora”
czyli
Na szczęście układ tych równań jest łatwo rozwiązać. Z trzeciego równania otrzymujemy równość \(z=x\). Wstawiamy to do drugiego równania, z którego wyznaczamy \(y\) i to wstawiamy do pierwszego równania. W wynku otrzymujemy:
Łatwo spoztrzegamy, że \(x=0\) spełnia trzecie równanie. wstawiając to do pierwszego i drugiego równania otrzymujemy \(y=0\) oraz \(z=0\). Tak więc mamy jeden stan stacjonarmy:
Pozostale stany stacjonarne są wyznaczone przez równania:
Z ostatniego równania wynika, że musi być spełnione równanie kwadratowe:
Wyróżnik tego równania jest zawsze dodatni:
Ponieważ wielkości stacjonarne to stężenia stacjonarne, więc są one dodatnie. Jedyny dodatni pierwiastek równania kwadratowego ma postać:
Badanie stabilności powyższych stanów stacjonarnych wymaga wyznaczenia wartości własnych macierzy Jacobiego, której wymiar wynosi 3. Oznacza to, że otrzymujemy wielomian 3-stopnia dla wartości własnej \(\lambda\). Mamy kilka możliwości:
wykonać obliczenia „na piechotę” (horror z kiepskim scenariuszem, patrz żmudne obliczenia w książce J. D. Murraya); to można zrobić relatywnie łatwo dla stanu stacjonarnego \((0, 0, 0)\), ktory okazuje się być zawsze niestabilny.
posiadać pewną wiedzę na temat pierwiastków wielomianów, jak np. kryterium Routha-Hurwitza albo reguła znaku Kartezjusza (drugi horror, ale scenariusz bardziej wyrafinowany)
zastosować SAGE - i to jest to!
Bedziemy badać stabilność niezerowego stanu stacjonarnego. W stanie tym ustala się stężenie trzech składników: X = [HBrO 2 ] , Y = [Br − ], Z = [Ce 4+ ].
Poniżej jest program, który możemy wykorzystać do „zabawy” jednocześnie się ucząc. Możemy zmieniać wartości różnych parametrów i warunków początkowych. Pamiętajmy, że stacjonarne wartości \(x\) oraz \(z\) są sobie zawsze równe: \(x=z\). Natomiast wartość \(y\) jest na ogół różniąca się.
Proponuję pozostawić wartości \(c, \delta=d, q\), a zmieniać wartość \(u\) oraz wartości początkowe początkowe \(x_0, y_0, z_0\), które są w drugim oknie poniżej. Taka „zabawa” wyrobi w nas intuicję, jaki jest wpływ poszczególnych elementów. Trzecie okno pozwala otrzymywać krzywą fazową na płaszczyżnie \((x, z)\).
Istotny jest zakres parametrów w okolicach
Można zaobserwować bifurkację Hopfa, czyli przejście od stałych wartości stacjonarnych do periodycznie zmieniających się w czasie, czyli oscylacji Biełousowa. Oscylacje te pojawiają się dla poniższych wartości parametrów w oknie wartościach parametru z grubsza z przedziału \(u \in (0.512, 2.35)\).
Proponuję taki ciąg zmian:
\(u=0.1, 0.3, 0.4, 0.5, 0.51, 0.5125, 0.5126, 0.5127 \quad \quad \quad (x_0, y_0, z_0) = (0.8, 0.2, 0.7), (0.08, 0.4, 0.07)\)
Zmieniaj dalej wartość parametru \(u\) do \(u \approx 2.35\) i dalej.
sage: var('x,y,z')
sage: c=0.04
sage: d=0.0004 ## to jest parametr delta
sage: q=0.0008
sage: u=0.512 ## zmiana tego parametru powoduje bifurkacje
sage: f(x,y,z)= (q*y -x*y + x -x*x)/c
sage: g(x,y,z)=(-q*y - x*y +u*z)/d
sage: h(x,y,z)= x-z
sage: T = srange(0, 30,0.001) ## tu można zmieniać czas zmieniając drugą wartość, czyli wydłużać wartość poziomej osi
sage: sol1=desolve_odeint([f,g,h], [0.08,0.5,0.07], T, [x,y,z]) ## w 2 nawiasie są warunki początkowe dla x, y, z
sage: line( zip ( T,sol1[:,2]) ,color='black',legend_label="z") +\
... line( zip ( T,sol1[:,0]) ,color='red',legend_label="x") ## + line( zip ( T,sol1[:,1]) ,color='green',legend_label="y")
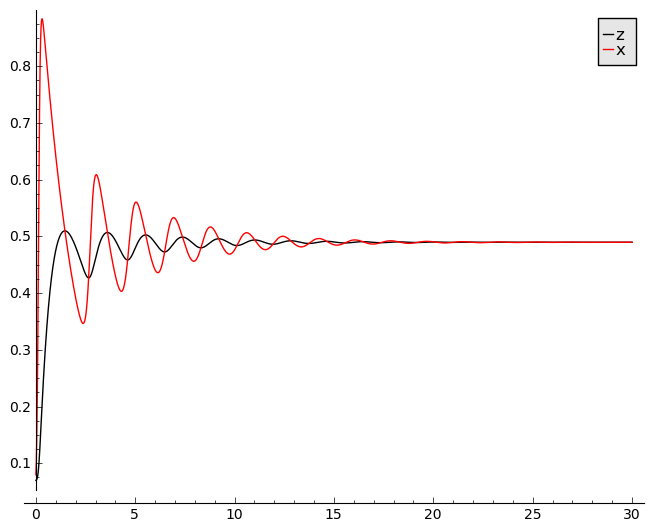
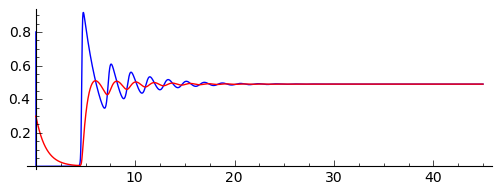
Powyżej przedstawiony jest przebieg czasowy koncentracji substancji \(x\) oraz \(z\).
Aby dołączyć do rysunku ewolucję zmiennej \(y\) należy w oknie powyżej zlikwidować symbol # # w dolnej linii. Czasami wartość \(y\) jest bardzo duża w relacji do pozostałych. W tym przypadku lepiej nie dokładać wykresu dla \(y\).
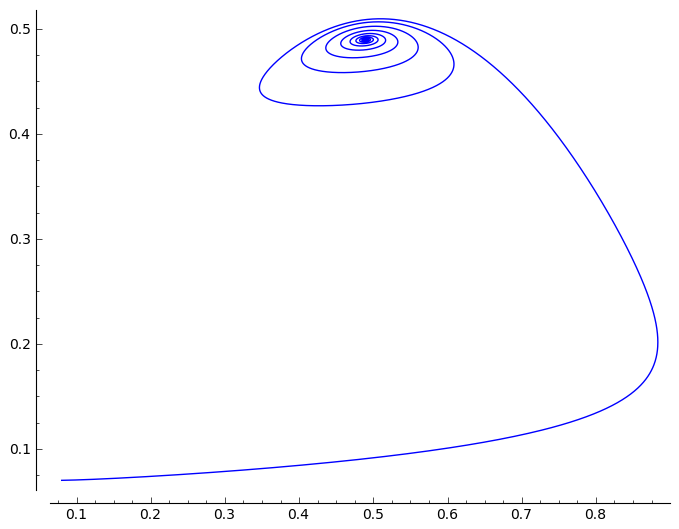
W poniższym oknie możemy obserwować kształt krzywej fazowej dla paramatrów z okna pierwszego i drugiego.
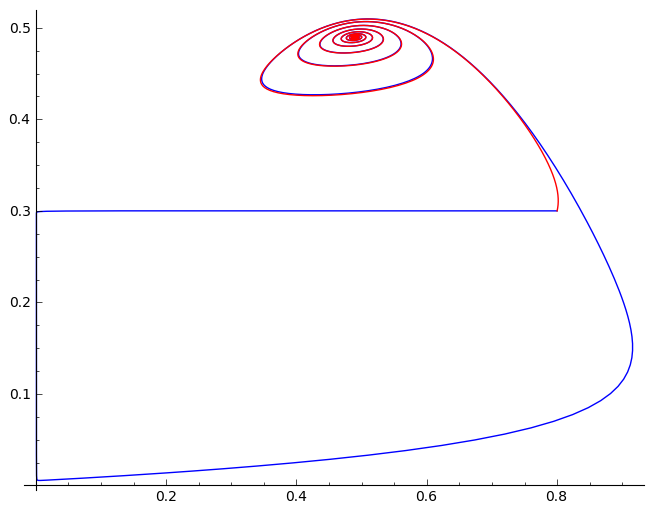
Zamkniętej krzywej fazowej odpowiadają rozwiązania periodyczne. W takim reżimie można obserwować oscylacje, które w 1951 roku odkrył Biełousow.
sage: X = sol1[:,0]
sage: Y = sol1[:,1]
sage: Z = sol1[:,2]
sage: list_plot(zip(X,Z), plotjoined=1)
Układ zredukowany \(\delta =0\)¶
Badanie stabilności „oregonatora” jest dość uciążliwe. Dokonamy teraz przybliżenia układu, dla którego badanie stabilności jest prostsze. Porównamy też wyniki dla pełnego układu i przybliżonego. Zobaczymy, czy pojawiają sie istotne różnice.
W drugim zestawie parametrów:
Zauważmy, że
i dlatego dokonamy przybliżenia \(\delta \approx 0\). Wówczas równania „oregonatora” są postaci:
Z drugiego równania wyznaczamy zmienną \(y\):
i wstawiamy do pierwszego równania otrzymując układ zredukowany:
Stany stacjonarne tego układu pokrywają się ze stanami stacjonarnymi pełnego układu. Tak więc mamy stan stacjonarmy:
Drugi stan stacjonarny określony jest przez równania:
Stan dla \(y\) jest wyznaczony przez równanie (1). Aby zbadać stabilność stanu określonego przez równanie (2), musimy zbadać wartości własne macierzy Jacobiego:
Wartości własne \(\lambda\) określone są przez równanie:
Stąd otrzymujemy równanie dla \(\lambda\). Jest to równanie kwadratowe:
Zauważamy, że \(A+D\) to ślad macierzy Jacobiego \({\text Tr} J\) , a wielkość \(A D - B C\) to wyznacznik macierzy \({\text Det} J\), czyli równanie to przepiszemy w postaci:
Pierwiastki tego równania są dane przez wzór:
Jeżeli przy zmianie parametrów pojawiają się relacje
to dwie wartości własne stają się liczbami urojonymi, czyli obserwuje się bifurkację Hopfa. Obliczamy pochodne cząstkowe funkcji \(F\) oraz \(H\). Warunek \({\text Tr} J = 0\) ma postać
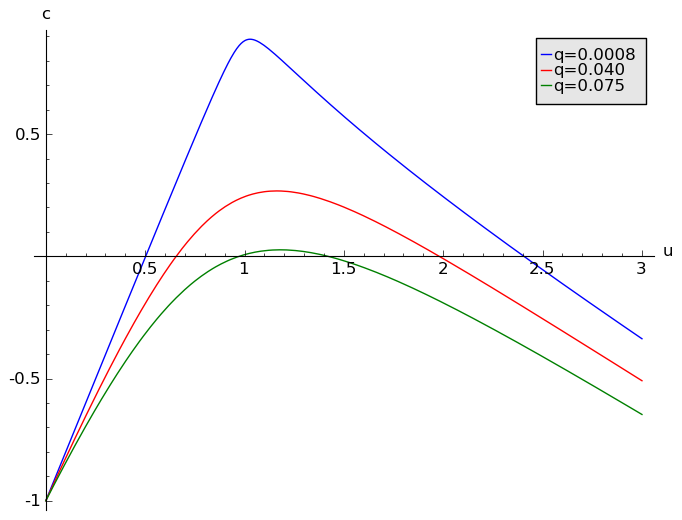
gdzie \(x\) jest wyznaczone przez równanie (2). Te dwa równanie, przy naszej ustalonej wartości \(q = 0.0008\), wyznaczają granicę rozwiązań oscylacyjnych. Na płaszczyźnie (u, c) otrzymujemy diagram bifurkacyjny dla zredukowanego układu. Dla wartości \((u \gt 0, c \gt 0)\) między krzywą a osią poziomą pojawiają się oscylacje. Jak widać z poniższego wykresu, zwiększanie wartości \(q\) powoduje zmiejszanie się obszaru parametrów \((u, c)\) dla których pojawiają się oscylacje. Powyżej pewnej wartości krytycznej \(q \gt q_c\) oscylacje zanikają całkowicie.
sage: var('u,q')
sage: D(u,q)=(1-q-u)^2 + 4*q*(1+u)
sage: x1(u,q)=0.5*(1-q-u+sqrt(D(u,q)))
sage: c(u,q)=1-2*x1(u,q) - 2*u*q*x1(u,q)/(q + x1(u,q))^2
sage: pr1=plot(c(u,0.0008), (u,0,3), legend_label="q=0.0008")
sage: pr2=plot(c(u,0.04), (u,0,3), color='red', legend_label="q=0.040")
sage: pr3=plot(c(u,0.075), (u,0,3), color='green', legend_label="q=0.075")
sage: show(pr1+pr2+pr3, ,fontsize=12 )
Wyprowadzenie powyższych wzorów wykorzystując algebrę komputerową:
sage: var('x u q c z')
sage: F(x, z) =( x*(1-x) + u*z*(q-x)/(q+x) )/c
sage: H(x,z)= x-z
sage: x0 = solve([F(x,z),H(x,z)],[x,z])[1][0].rhs()
sage: J = jacobian(vector([F,H]),(x,z) )
sage: print "Tr(J) łatwo rozwiazać na c!"
sage: show(J.trace())
sage: Tr(u,q,c) = J.trace().subs({x:x0,z:x0})
sage: C(u,q) = Tr(u,q,c).solve(c)[0].rhs().simplify()
Tr(J) łatwo rozwiazać na c!
sage: sum([plot(C(u,q_),(u,.01,3),figsize=(6,4),axes_labels=['u','c'],legend_label="q=%0.4f"%q_) for q_ in srange(0.0001,0.2,0.02) ] )
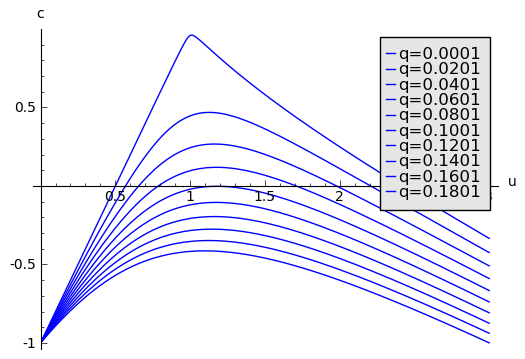
Obszar pod czerwoną krzywą zawiera miejsca gdzie Tr(J)>0 co sugeruje oscylacje (punkt stały jest niestabilny).
sage: contour_plot(C(u,q),(u,.01,3),(q,1e-6,.1), axes_labels=['u','q'],contours=srange(0,.61,0.01),aspect_ratio=30.)+\
... implicit_plot(C(u,q),(u,.01,3),(q,1e-6,.1), axes_labels=['u','q'],color='red')
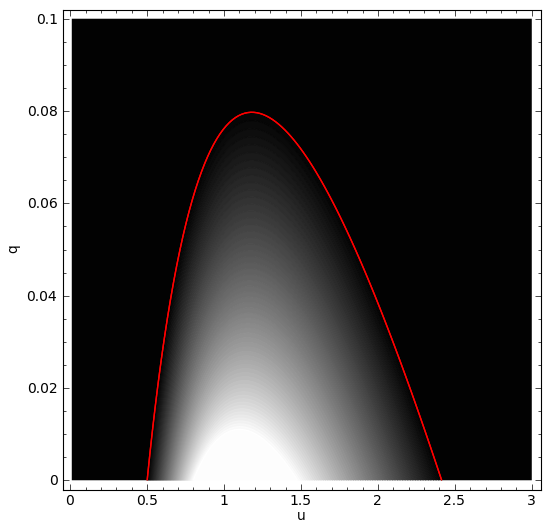
Porównanie rozwiązań pełnego „Oregonatora” i układu zredukowanego¶
sage: var('x,y,z')
sage: c=0.04
sage: d=0.0004 ## to jest parametr delta: zmieniaj go od małej wartości, np. 0.0004 (brak różnic) do np. 0.04 (obserwuje się różnice)
sage: q=0.0008
sage: u=0.51 ## zmieniaj też ten parametr bifurkacyjny
sage: f(x,y,z)= (q*y -x*y + x -x*x)/c
sage: g(x,y,z)=(-q*y - x*y +u*z)/d
sage: h(x,y,z)= x-z
sage: T = srange(0, 30,0.001) ## tu można zmieniać czas zmieniając drugą wartość, czyli wydłużać wartość poziomej osi
sage: sol1=desolve_odeint([f,g,h], [0.08,0.5,0.07], T, [x,y,z]) ## w 2 nawiasie są warunki początkowe dla x, y, z
sage: var('x z')
sage: c=0.04
sage: q=0.0008
sage: u=0.51 ## zmieniaj tę wartość
sage: F(x, z) =(1/c)*( x*(1-x) + u*z*(q-x)/(q+x) )
sage: H(x,z)= x-z
sage: Ts = srange(0, 30,0.001) ## tu można zmieniać czas zmieniając drugą wartość, czyli wydłużać wartość poziomej osi
sage: solR=desolve_odeint([F,H], [0.08,0.07], Ts, [x,z]) ## w 2 nawiasie są warunki początkowe dla x, y, z
sage: line( zip ( T,solR[:,0]),legend_label="zredukowany" )+line( zip ( T,sol1[:,0]), color='red',legend_label="Oregonator")
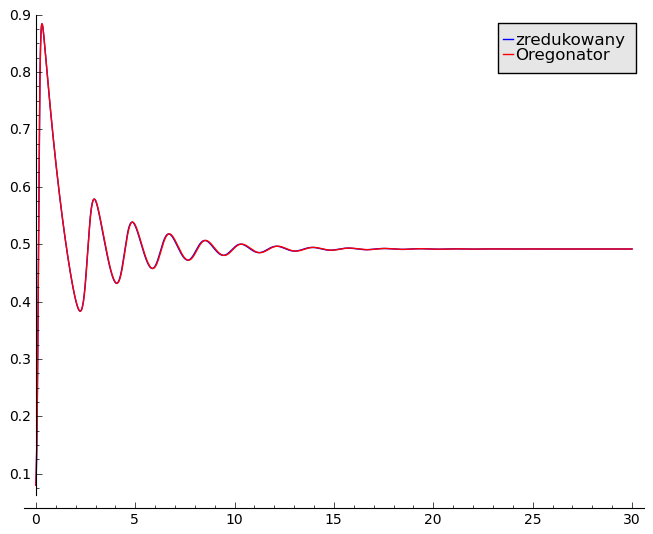
Demostracja użycia CAS do selektywnego uproszczenia wzorów¶
sage: tr = J(x,x).trace()
sage: show(tr)
sage: show( tr.operands()[0] )
sage: show( tr.operands()[0].operands() )
sage: show( (-tr.operands()[0].operands()[0]) )
sage: show( (-tr.operands()[0].operands()[0]).operands() )
sage: show( (-tr.operands()[0].operands()[0]).operands()[0:2] )
sage: show(sum( (-tr.operands()[0].operands()[0]).operands()[0:2] ).factor() )
sage: print "Ma być:"
sage: show( 1-2*x - 2*u*q*x/(q + x)^2 )
Ma być:
Diagram bifurkacyjny układu zredukowanego \(x^*(q)\)¶
sage: var('x u q c z')
sage: F(x, z) =( x*(1-x) + u*z*(q-x)/(q+x) )/c
sage: H(x,z)= x-z
sage: x0 = solve([F(x,z),H(x,z)],[x,z])[1][0].rhs()
sage: J = jacobian(vector([F,H]),(x,z) )
sage: Tr(u,q,c) = J.trace().subs({x:x0,z:x0})
sage: C(u,q) = Tr(u,q,c).solve(c)[0].rhs().simplify()
Narysujmy jak zmienia sie punkt stały z \(q\) przy ustalonych pozostałych parametrach. Kolorem czerwonym zaznaczamy punkt stały niestabilny (\({\text Tr} J \gt 0\)) a niebieskim stabilny.
sage: fix_stable = []
sage: fix_unstable = []
sage: for q_ in srange(.0001,.1,0.0002):
... pars = {c:0.3,q:q_,u:1.1}
... if Tr(u,q,c).subs(pars)<0:
... fix_stable.append((q_,x0.subs(pars)))
... else:
... fix_unstable.append((q_,x0.subs(pars)))
sage: point( fix_stable)+point( fix_unstable,color='red')
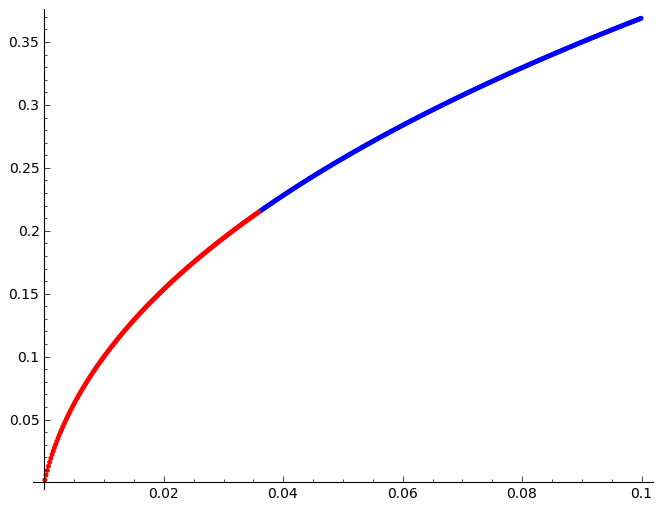
Niestabilny punkt stały i brak innych stabilnych punktów sugeruje możliwość rozwiązań okresowych typu cykl graniczny.
Powtarzając poprzedni algorytm, jeśli punkt jest niestabilny
rozwiązujemy ODE
nanosimy na diagramie ekstremalne wartości trajektorii \(x(t)\) po pewnym czasie umożliwiającym relaksację warunku początkowego.
dodatkowo rysujemy trajektorię na prawym rysunku z wyróżnieniem ostatnich stu punktów. Trajektorią jest wyliczana dla \(t\in(0,T_{end}).\)
sage: fix_stable = []
sage: fix_unstable = []
sage: times = srange(1,125,.2)
sage: IC = (.51,.51)
sage: print "wyliczam diagram bifurkacyjny - chwilka..."
sage: for q_ in srange(.0001,.1,0.002)+srange(.035,.038,0.00001):
... pars = {c:0.3,q:q_,u:1.1}
...
... if Tr(u,q,c).subs(pars)<0:
... fix_stable.append((q_,x0.subs(pars)))
... else:
... sol=desolve_odeint([F.subs(pars),H.subs(pars)],IC,times,[x,z])
... X = sol[sol.shape[0]/2:,0]
... fix_stable.append((q_,X.min()))
... fix_stable.append((q_,X.max()))
... fix_unstable.append((q_,x0.subs(pars)))
sage: print "ok"
sage: @interact
sage: def _(qsel =slider(0.03,0.041,0.000001,default= 0.037),Tend=slider(10,100000,0.1,default= 120)):
... pars[q]=qsel# = {c:0.3,q:qsel,u:1.1}
... times = srange(1,Tend,.2)
... sol=desolve_odeint([F.subs(pars),H.subs(pars)],IC,times,[x,z])
... html.table([[point( fix_stable)+point( fix_unstable,color='red',gridlines=[[qsel],[]]),line(sol)+line(sol[-20:,:],color='red')]])
sage: times = srange(1,125,.2)
sage: IC = (1,1)# (x0.subs(pars),x0.subs(pars)+1e-3)
sage: sol=desolve_odeint([F.subs(pars),H.subs(pars)],IC,times,[x,z])
sage: X = sol[sol.shape[0]/2:,0]
sage: X.min()
sage: X.max()
sage: X = sol[sol.shape[0]/2:,0]#- x0.subs(pars).n()
sage: print X.min(),X.max()
sage: list_plot(list(X))
0.0500712624079 0.506595108388
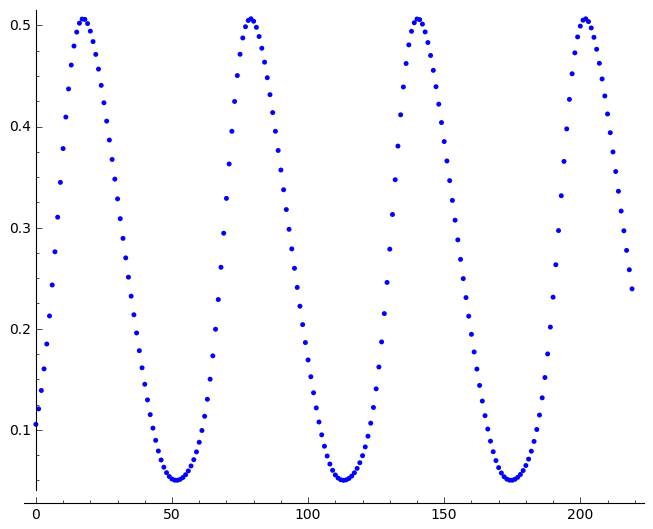
sage: line(zip(times,sol[:,1]),gridlines=[[],[x0.subs(pars).n()]])
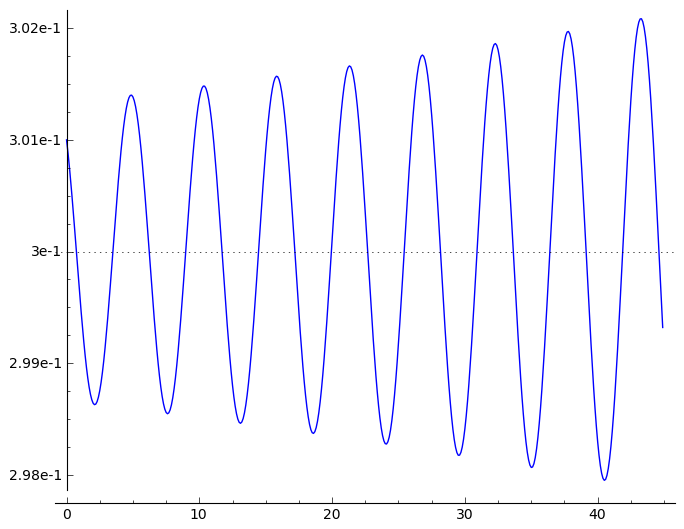
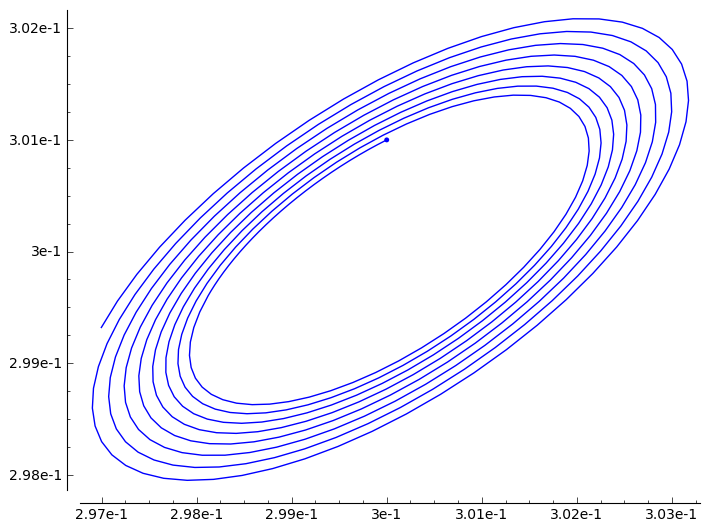
sage: line(sol)+point(IC)
sage: pars = {c:0.04,q:0.0008,u:0.8}
sage: fix_pointsR = solve([F.subs(pars),H.subs(pars)],x,z,solution_dict=True)
sage: plt_fpR = point( [ (x.subs(fp).n(),z.subs(fp).n()) for fp in fix_pointsR],color='red')
sage: plt_fpR
sage: pars = {c:0.04,d:0.0002,q:0.0008, u:0.8}
sage: fix_points = solve([f.subs(pars),g.subs(pars),h.subs(pars)],x,y,z,solution_dict=True)
sage: plt_fp = point( [ (z.subs(fp).n(),z.subs(fp).n()) for fp in fix_points],color='red')
sage: times = srange(0,0.1,.0001)+srange(0.1,1.0,.001)+srange(1,45,.01)
sage: IC = [0.8,120.2,.3]
sage: sol=desolve_odeint([f.subs(pars),g.subs(pars),h.subs(pars)],IC,times,[x,y,z])
sage: p=line(zip(times,sol[:,0])) + line(zip(times,sol[:,2]),color='red')
sage: p.show(figsize=(6,2))
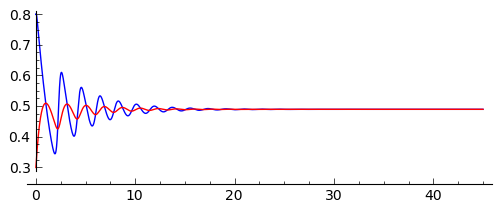
sage: solR=desolve_odeint([f1.subs(pars),h1.subs(pars)],[IC[0],IC[2]],times,[x,z])
sage: p=line(zip(times,solR[:,0]))+line(zip(times,solR[:,1]),color='red')
sage: p.show(figsize=(6,2))
Porównanie układu 2d i 3d:
sage: line(zip(sol[:,0],sol[:,2]))+line(zip(solR[:,0],solR[:,1]),color='red')
sage: surf = implicit_plot3d((-q*y - x*y + u*z).subs(pars),(x,0,1),(y,0,230),(z,0,.4))
sage: traj = line(zip(sol[::1,0],sol[::1,1],sol[::1,2]),color='red',thickness=9)
sage: plt_IC = point(IC,size=20,color='yellow')
sage: surf+traj+plt_IC
Traceback (most recent call last):
...
NameError: name 'y' is not defined
sage: surf_form=solve(-q*y - x*y + u*z,y)[0].rhs().subs(pars)
sage: show(surf_form)
sage: solR_3d = [(x,surf_form(z=z,x=x),z) for x,z in solR]
sage: trajR = point(solR_3d,color='green',size=14)
sage: surf+traj+plt_IC+trajR
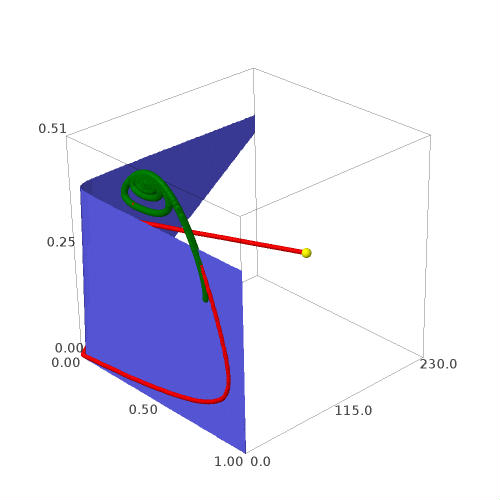
sage: fp_n = [ (x.subs(fp).n(),z.subs(fp).n()) for fp in fix_pointsR]
sage: html.table(fp_n )
−0.604242327531896
−0.604242327531896
0.00344232753189605
0.00344232753189605
0.000000000000000
0.000000000000000
sage: var('x z')
sage: vf = vector( [f1.subs(pars),h1.subs(pars) ])
sage: vf = vf/vf.norm()
sage: domx,domy =(x,-0.0020,0.01),(z,-0.002,.014)
sage: plt_fp = point( fp_n[1:],color='red',size=30)
sage: vec_plt = plot_vector_field( vf, domx,domy)
sage: nullc1=implicit_plot( f1.subs(pars), domx,domy)
sage: nullc2=implicit_plot( h1.subs(pars), domx,domy)
sage: vec_plt+plt_fp+nullc1+nullc2
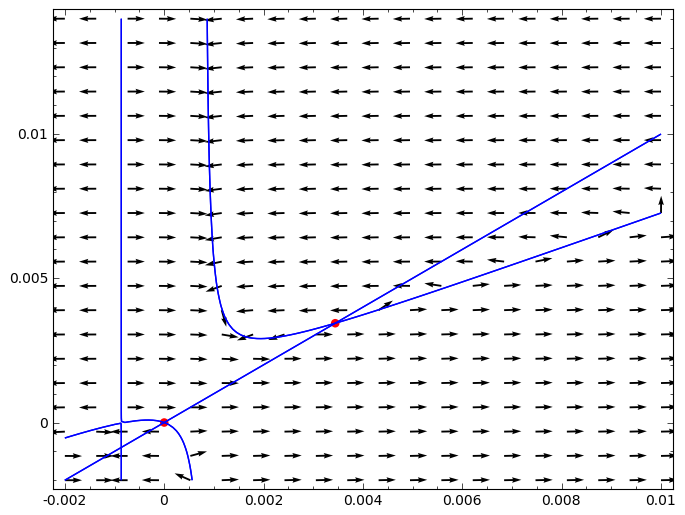
sage: for x_,z_ in fp_n:
... print x_,z_
... A = jacobian([f1.subs(pars),h1.subs(pars) ],[x,y])(x=x_,z=z_)
... show(A)
...
... print map(N,A.eigenvalues())
... print A.eigenvectors_right()
-0.604242327531896 -0.604242327531896
[55.3183153770813, 0.000000000000000] [(56480/1021, [], 1), (0, [(0, 1)], 1)]
0.00344232753189605 0.00344232753189605
[12.5866900175131, 0.000000000000000] [(7187/571, [], 1), (0, [(0, 1)], 1)]
0.000000000000000 0.000000000000000
[0.000000000000000, 25.0000000000000] [(0, [(0, 1)], 1), (25, [(1, 1/25)], 1)]
sage: m=matrix(QQ,[[12.5966,0],[1,0]])
sage: m
sage: m.eigenvectors_right()
sage: var('y')
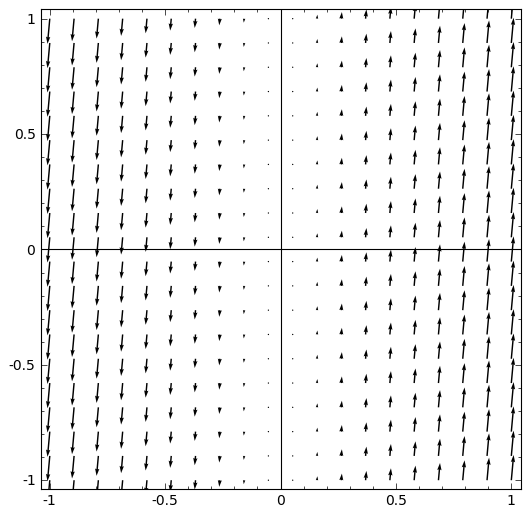
sage: plot_vector_field(m*vector([x,y]),(x,-1,1),(y,-1,1))
Rozwiązania spiralne w układzie reakcji z dyfuzją (Bielousow-Zabotyński)¶
sage: a=1.0
sage: b=0.1
sage: eps=0.1
sage: a = 0.75
sage: b = 0.0006
sage: eps = 0.072
sage: var('u v')
sage: f(u,v) = u*(1-u)*(u-(v-b)/a)
sage: g(u,v) = u-v
sage: V = vector( (1/eps*f,g))
sage: V=V/V.norm()
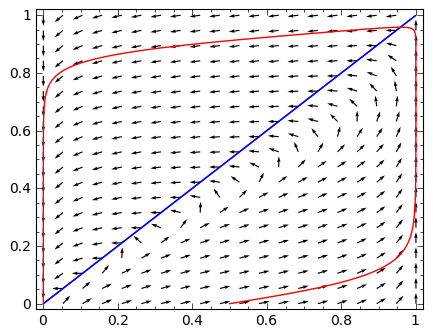
sage: vfield=plot_vector_field(V,(u,0,1),(v,0,1))+implicit_plot(g,(u,0,1),(v,0,1))
sage: t = srange(0,4/eps,0.01)
sage: sol = desolve_odeint([19*f,g], [0.5,0.0], t, [u,v])
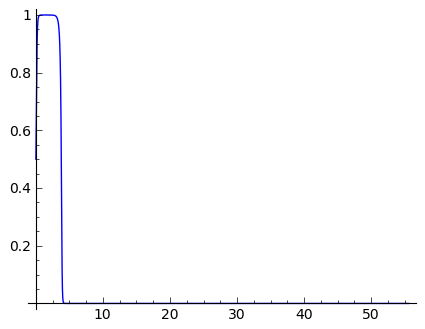
sage: plt_phase = vfield+line(sol,color='red',figsize=5)
sage: plt_time = line(zip(t,sol[:,0]),figsize=5)
sage: html.table([[plt_phase,plt_time]])
sage: %timeit
sage: import numpy as np
sage: sparse = True
sage: slicing = True
sage: Dyf_u = 1.0
sage: Dyf_v = 0.052
sage: Dyf = max(Dyf_u,Dyf_v)
sage: a = 1.0
sage: b = 0.001
sage: eps = 0.072
sage: l = 100.0 # dlugosc ukladu
sage: t_end = 100 # czas symulacje
sage: N = 160 # dyskretyzacja przestrzeni
sage: h = l/(N-1)
sage: dt = 0.052/(Dyf*(N-1)**2/l**2) # 0.2 z warunku CFL, krok nie moze byc wiekszy
sage: dt_dyn = (1.0/eps)/125.0
sage: sps = int(1/dt) # liczba krokow na jednostke czasu
sage: Nsteps=sps*t_end # calkowita liczba krotkow
sage: print "dt,dt_dyn",dt,dt_dyn
sage: dt = min(dt,dt_dyn)
sage: print "sps=",sps,"dt=",dt,'Nsteps=',Nsteps
sage: # warunek poczatkowy
sage: u = np.zeros((N,N))
sage: v = np.zeros((N,N))
sage: #u[int(N/2)-5:int(N/2)+5,int(N/2)-5:int(N/2)+5]=1 # step
sage: #u[:int(N/2)+5,:]=1.0 # step
sage: #u[int(N/2)-5:int(N/2)+5,int(N/2)-20:int(N/2)+20]=1.0
sage: #v[int(N/2)-5:int(N/2)+3,int(N/2)-20:int(N/2)+20]=1.0
sage: #u[int(N/2)-5:int(N/2)+5,int(N/2)-20:int(N/2)+20]=1.0
sage: #v[int(N/2)-5:int(N/2)+5,int(N/2)-22:int(N/2)+18]=1.0
sage: #u[-20:-1,int(N/2)-5:int(N/2)+5]=1.0
sage: #v[-20:-1,int(N/2)-6:int(N/2)+4]=1.0
sage: #u[:5,:]=1.0
sage: #v[:4,:]=1.0
sage: #u[-10:,:]=1.0
sage: #v[-4:,:]=1.0
sage: u[:int(N/2),int(N/2)-5:int(N/2)+5]=1.0
sage: v[:int(N/2),int(N/2)-6:int(N/2)+4]=1.0
sage: # aby wymusic ruch falowy, przesuwamy u wzgledem v
sage: def essential_boundary_conditions(u):
... u[:,0] = 0.0
... u[:,-1] = 0.0
... u[-1,:] = 0.0
... u[0,:] = 0.0
... v[:,0] = 0.0
... v[:,-1] = 0.0
... v[-1,:] = 0.0
... v[0,:] = 0.0
...
sage: Tlst=[]
sage: Tvlst=[]
sage: essential_boundary_conditions(u)
sage: for i in range(Nsteps):
... if not i%sps:
... Tlst.append(u.copy())
... Tvlst.append(v.copy())
...
... u[1:-1,1:-1] = u[1:-1,1:-1] + dt*(1.0/eps*u[1:-1,1:-1]*(1-u[1:-1,1:-1])*( u[1:-1,1:-1]-(v[1:-1,1:-1]+b)/a ) + \
... Dyf_u*(N-1)**2/l**2*(np.diff(u,2,axis=0)[:,1:-1]+np.diff(u,2,axis=1)[1:-1,:]))
... v[1:-1,1:-1] = v[1:-1,1:-1] + dt*( (u[1:-1,1:-1]-v[1:-1,1:-1]) )
... # + \
... # Dyf*(N-1)**2/l**2*(np.diff(v,2,axis=0)[:,1:-1]+np.diff(v,2,axis=1)[1:-1,:]))
... essential_boundary_conditions(u)
...
sage: print "Saved ",len(Tlst), " from ", Nsteps
sage: anim=animate([matrix_plot(u,cmap='jet',figsize=(4,4)) for u in Tlst[:]])
sage: anim.show()
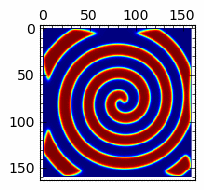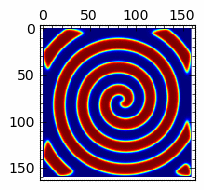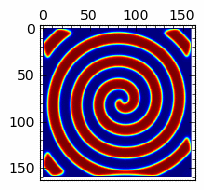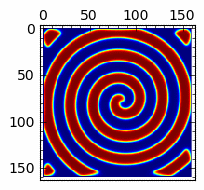
sage: import pylab
sage: @interact
sage: def _(ti=slider(range(len(Tlst)))):
... print r"t=",dt*ti*sps
... if True:
... pylab.subplot(1,2,1)
... pylab.imshow(Tlst[ti],vmin=0,vmax=1,origin='top')
... pylab.subplot(1,2,2)
... pylab.imshow(Tvlst[ti],vmin=0,vmax=1,origin='top')
... pylab.savefig('1.png',dpi=70)
... else:
... p = matrix_plot(Tlst[ti])
... p.show(figsize=(4,4))
sage: anim=animate([matrix_plot(u,cmap='jet',figsize=(2,2)) for u in Tlst[40:72:2]])
sage: anim.show()