Jak skomplikować proste i popaść w kłopoty z funkcją tangens

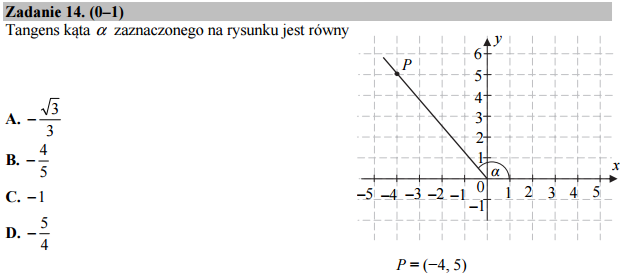
Wynik otrzymujemy natychmiast bez komputera metodą przez „ogląd”:, łatwo widać, że ostatnia odpowiedz jest prawdziwa. Mówiąc inaczej korzystamy z definicji tangensa: \(tan(\alpha)=\frac{y}{x}\) dla \(x=-4\) i \(y=5\).

Wyobraźmy sobie jednak, że zapomnielismy co to tangens, ale pamiętamy, że Sage posiada funkcję odwrotną arctan, która pozwoli nam rozwiązać zadanie „od końca” przez wyliczenie kątów i narysowanie wszystkie odpowiedzi w tescie. Będziemy do tego potrzebowali jeszcze odległości od początku układu wspólrzędnych, którą wyliczymy z Twierdzenie Pitagorasa: \(r=\sqrt{x^2+y^2}=\sqrt{5^2+4^2}\). Z definicji sinusa i cosinusa wiemy też, że współrzędne spełniają:

\[\begin{split}x = r \cos(\phi) \\ y = r \sin(\phi)\end{split}\]

Wystarczy więc dla każdej odpowiedzi z testu obliczyć kąt i narysować odpowiadający punkt na wykresie (np. funkcją point((x,y)). Właściwą odpowiedź rozpoznamy graficznie.

Nasuwa się pytanie: czy można jeszcze bardziej skomplikować to zadanie?

Napiszmy więc:

Jednak wykres nie jest zbyt piękny, fajnie by było ustawić takie same zakresy osi jak w zadaniu. Aby precyzyjnie odczytać położenie punktu z wykresu dorysujemy też siatkę z lini pionowych i poziomych gridlines.

No to mamy już nasz program gotowy, dodajemy jeszcze @interact by sprawdzać odpowiedzi kliknięciem w odpowiedni klawisz:

Co się okazuje, żadna odpowiedź daje punktu w tym samym miejscu jak w zadaniu? Co poszło nie tak?

Okazuje się że zawiniła właność funkcji \(\tan\). Jej okres to \(\pi\) - a nie \(2 \pi\) jak u poczciwego sinusa. Oznacza to, że jeżeli:

\[a = \tan(\phi),\]

to także zachodzi:

\[a = \tan(\phi+\pi)\]

Czyli działając funkcją odwrotną:

\[\arctan(a) = \phi+\pi!\]

Dodajmy więc do naszego rysunku drugi punkt dlą kąta \(\phi+\pi\):

I zgadza się! W ostatnim przypadku otrzymujemy wszystkie punkty dla których \(\tan(\phi)=-\frac{5}{4}\) i \(r=\sqrt{41}\). Jednym z tych punktów jest ten z rysunku w zadaniu.

Jak to działa: gridlines

Opcja gridlines pozwala na narysowanie pionowych i poziomych lini na dowolnym wykresie w Sage. Składnia wygląda tak:

gridlines = [ [x1,x2,...,xn], [y1,y2,...,yn] ]

gdzie x1,x2,… to położenia prostych pionowych a y1,y2,… poziomych. Jest to zagnieżdżona lista, dwuelementowa, na której znajdują się dwie listy ze współrzędnymi. Przykłady:

• gridlines=[[1,2,5],[]] - trzy linie pionowe

• gridlines=[ range(1,20),[3]] - 19 lini pionowych i jedna pozioma