Narzędzia i metody pracy¶
Technologiczne aspekty korzystania z SageMath¶
Czym jest SageMath¶
Pakiet SageMath jest wolnym i otwartym (GNU GPL) oprogramowaniem matematycznym. Został on oparty na języku Python i oferuje pełne spektrum interfejsów dostępu, począwszy od terminala tekstowego po interfejs graficzny wykorzystujący przeglądarkę internetową.
SageMath jest dystrybuowany jako dość pokaźny pakiet instalacyjny (ok 1GB), zawierający następujące narzędzia:
Python 2.7
NumPy
SciPy
matplotlib
Sympy
Maxima
GAP
FLINT
R
Ambicją grupy programistów tworzących SageMath jest stworzenie pełnowartościowej otwartej alternatywy dla komercyjnych pakietów: Magma, Maple, Mathematica oraz Matlab.
Linia poleceń¶
Terminal tekstowy jest tradycyjną metodą korzystania z systemów komputerowych. Pomimo, że terminal jest technologią sięgającą swych początków w latach siedemdziesiątych XX wieku, to sposób pracy ugruntował sobie miejsce w nowoczesnych świecie technologii informatycznych. Współczesnie, terminal to tak zwany softwarowy emulator terminala tekstowego. Sposób korzystania jest oparty na koncepcji edycji pojedyńczej linii i wysłania jej do wykonania programowi, który jest uruchomiony. Przykładem może być powłoka systemu operacyjnego (windows shell, bash) lub interpreter Pythona lub SageMath. Praca w takim trybie jest szczególnie przydatna podczas eksploracji naukowych i jest powszechnie stosowania na całym świecie.
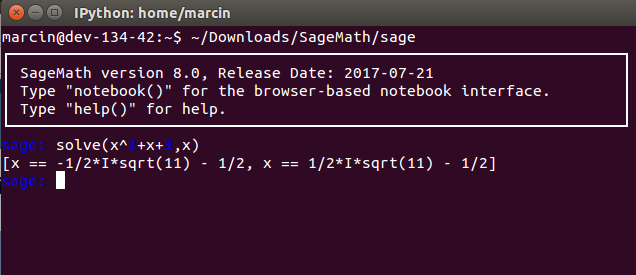
Rys. 7 Przykładowa sesja w linii poleceń w systemie SageMath.¶
Notatnik¶
System typu notatnik łączy w sobie dwie koncepcje. Pierwszą jest dokument zawierający bogaty (np. ilustrowany) sformatowany tekst oraz kod programu komputerowego. Ponadto tzw. wyjscie programu może być zarówno tekstem (jak w przypadku terminala tekstowego) jak i formułą, rysunkiem czy też interaktywnych elementem (np. suwakiem). Drugą koncepcją jest system dostępny przez przeglądarkę internetową pozwalającą na edycję powyższego dokumentu i wykonywanie zawartych w mim bloków kodu.
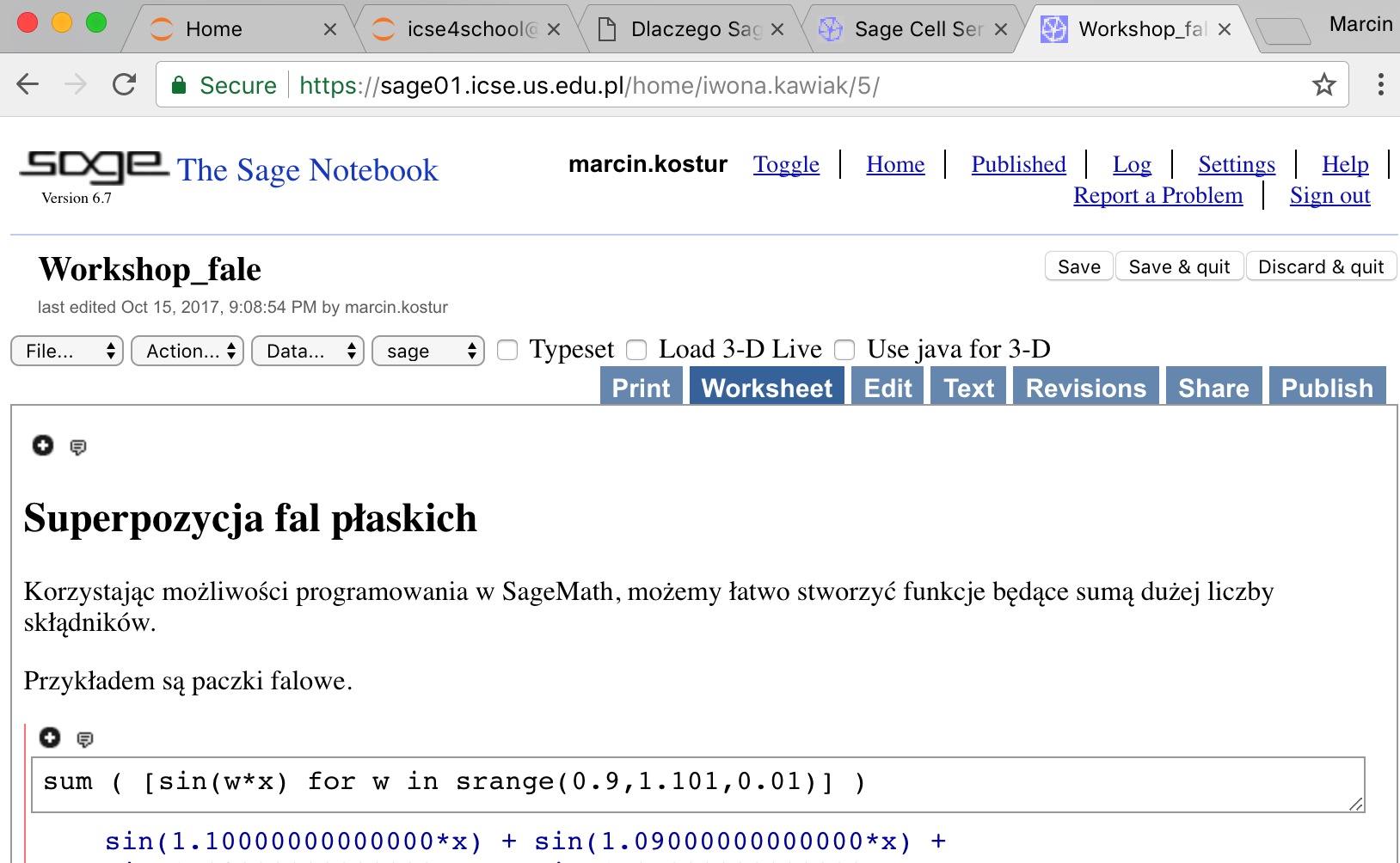
Rys. 8 Przykładowy notebook w systemie SageMath.¶
W projekcje iCSE4school notatnik SageMath (tzw. sagenb) był podstawowym narzędziem pracy. Jako aplikacja „webowa” oferował on dwa sposoby pracy:
praca w „chmurze” - korzystanie ze wspólnego serwera notatników skonfigurowanego dla szkół partnerskich.
praca lokalna na na własnej instalacji SageMath zawierająca notatnik sagenb.
Pierwszy sposób pracy oferuje oprócz samego notatnika system logowania, uwspólniania dokumentów oraz zarządzania kontami. Okazało się to bardzo przydatne w pracy na lekcji. Uczeń i nauczyciel mając jakiekolwiek urządzenie z dostępem do internetu mógł bez wykonywania żadnych instalacji oprogramowania w dowolnej chwili rozpocząć pracę z SageMath. Podandto bradzo przydatną cechą była możliwość uwspólniania notatników i ich publikacji. Na przykład można podejrzeć listę tzw. opublikowanych prac nauczycieli i uczniów na serwerach:
Interaktywne strony internetowe: system SageMathCell¶
Oprogramowanie SageMathCell umożliwia umieszczenie na dowolnej stronie internetowej okienka z kodem w SageMath z możliwością jego interaktywnego uruchamiania przez użytkowników (patrz rys. Rys. 9.). Wykonanie kodu nie wymaga logowania się co znakomicie deleguje tą technologie to zastosowań jako element w materiałach interaktywnych umieszcznych online. W przeciwieństwie do większości rozwiązań w których obliczenia wykonywane są po stronie klienta, SageMathCell korzysta z zainstalowanej centralnie instancji SageMath. Zaletą takiego rozwiązania jest bezkompromisowy dostęp do pełnej funkcjonalności SageMath z pośrednictwem dowolnego urządzenia.
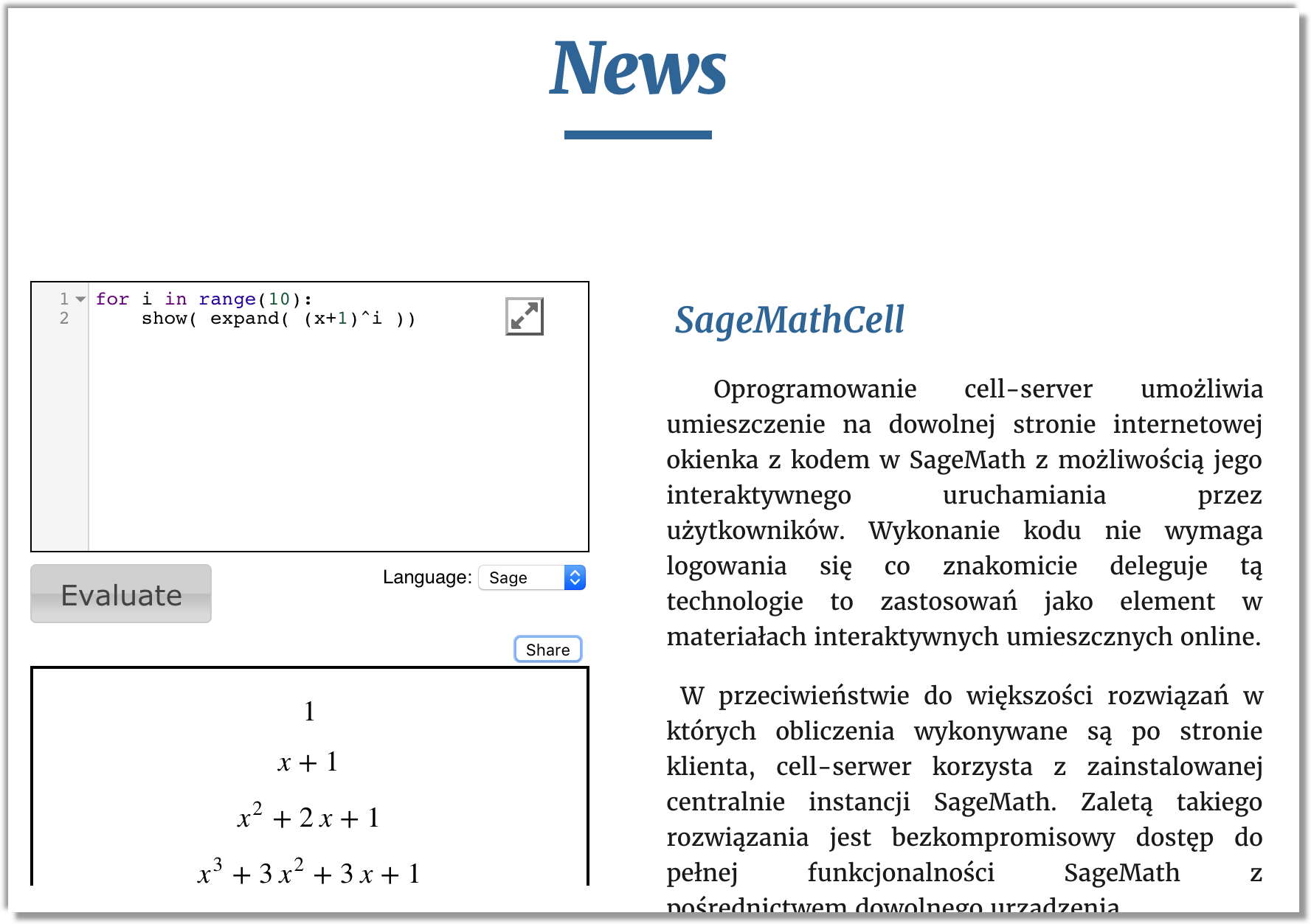
Rys. 9 Przykładowa strona (dla przykładu stworzona w google sites) zawierająca iframe z zanurzonyą komórką SageMathCell.¶
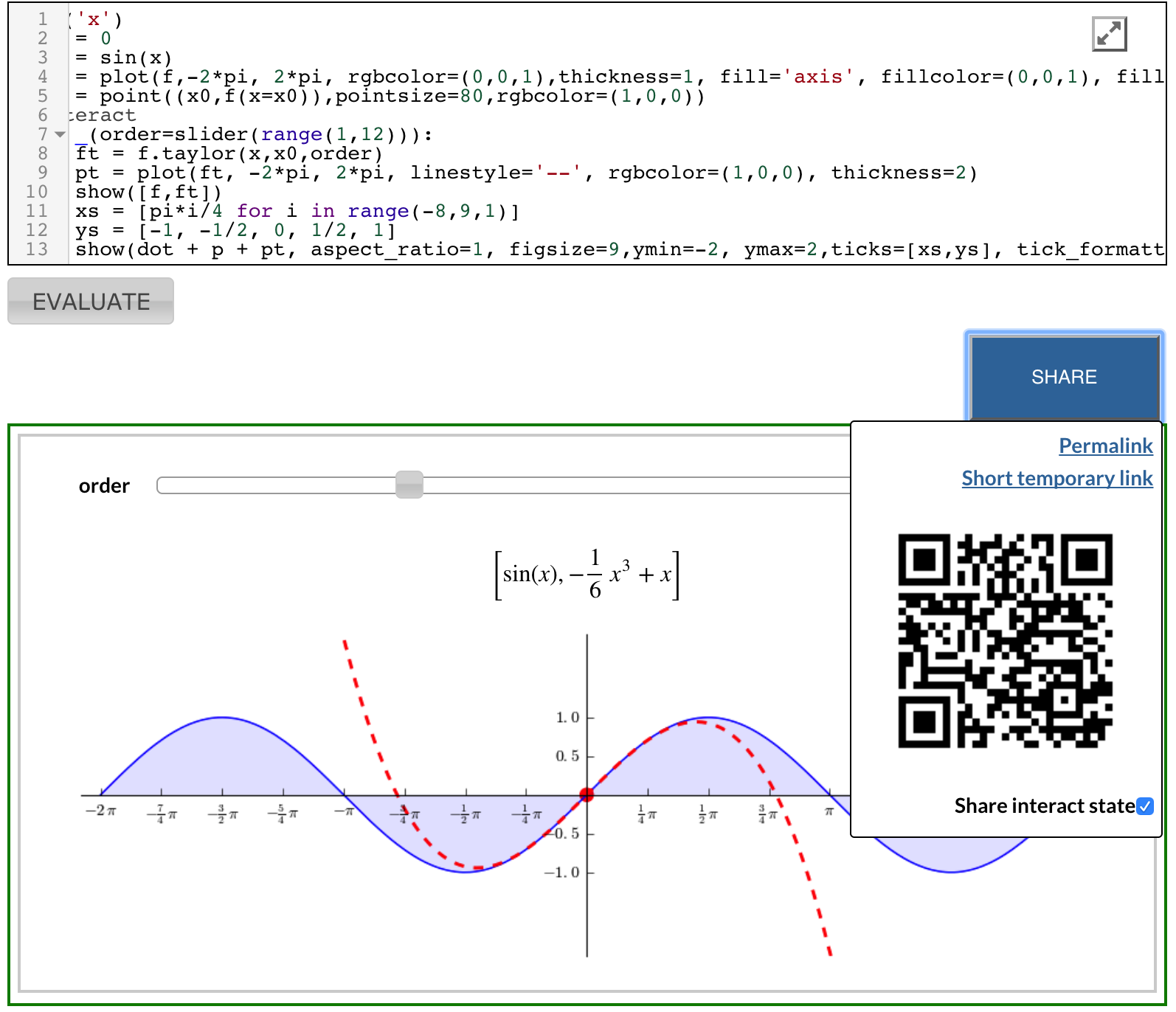
Rys. 10 Przykładowy element typu interact uruchomiony w systemie cell-server. Widoczne jest pojedyńcze okno z kodem programu a poniżej wynik jego działania: interaktywny suwak i wykres. Po prawej stronie rysunku widzimy możliwość stworzenia linku zawierającego powyższy program. Kod QR zawiera ten sam link. Link występuje w dwóch postaciach, krótkiej i długiej - zawierającej w url spakowany cały kod.¶
SageMathCell różni się tym od notatnika SageMath, że nie posiada możliwości zapisu edytowanego kodu. Istnieje jednak możliwość odtworzenia całej komórki wraz z kodem za pomocą linka (patrz rys. Rys. 10). Przekazanie takiego linka może odbyć się za pomocą kodu QR i wystarczy telefon komórkowy z dostępem do internetu by moć kod ten wykonać i edytować.
Stosowanie SageMath w praktyce szkolnej¶
Podczas pracy z SageMath w trakcie projektu iCSE4school, wykrystalizowało się kilka sposobów jego użycia. Po pierwsze dostęp przez konsolę - jako najbardziej zaawansowany - nie został użyty. Powszechnie stosowano notatnik sagenb. Spotkał się on z bardzo pozytywnym przyjęciem przez zarówno uczniów jak i nauczycieli. W naturalny sposób nauczyciele używali go do różnych celów. Można wyróżnić następujace rodzaje pracy:
Praca wyłącznie z komórkami z kodem Sage lub Python. W tym trybie notatnik praktycznie pełnił rolę oprogramowania znanego pod nazwą IDE (Integrated Development Environment). Jest to oprogramowie umożliwiające pisanie i wykonywanie kodu.
Intensywne użycie komórek tekstowych i narzędzi formatowania tekstu. W tym trybie zdarzało się wykorzystywać notatnik Sage jako edytor tekstu. Przydatną cechą okazała się możliwość opublikowania i uwspólniania dokumetnów na serwerze.
Stosowanie zarówno komórek tekstowych ji kodu. Duża część notatników zapisanych przez uczniów zalicza się do tej kategorii. Jednym z przykładów takiego użycia są sprawozdania z pracowni fizycznej.
Trzecia metoda interakcji z SageMath - cell server była stosowana podczas tworzenia materiałów - takich jak na przykład ten manuskrypt.
Należy zdecydowanie stwierdzić, że centralna instalacja serwera notatników jest bardzo przydatnym rozwiązaniem. Wpisująca się najnowsze trendy praca w „chmurze” ma następujące zalety dla użytkowników:
Wszechobecność materiałów. Można pracować w systemie SageMath wszędzie tam gdzie jest przeglądarka internetowa. Dzięki dostępności taniego internetu mobilnego jest to warunek spełniony praktycznie wszędzie.
Mniejsze ryzyko utraty danych przez zwykłe zgubienie lub awarię dysku twardego. Oczywiście to tego niezbędny jest sprawny system kopii zapasowowych działający na instalacji chmurowej. W naszym przypadku zastosowano rozwiązanie umożliwiające zapis codziennego stanu serwera. W przypadku całkowitego zniszczenia serweru lub np. skasowania danych przez złośliwe oprogramowanie czy cyberatak, można było odtworzyć stan dokumentów z dowolnego dnia przed tym wydarzeniem.
System notatnik «sagenb» ma cechy systemu e-learningowego, umożliwia dystrybuję materiałów, możliwy jest wgląd nauczyciela w pracę ucznia oraz tzw. publikacja materiałów przez zarówno uczniów jak i nauczycieli. Zaobserwowano intesywne wykorzystywanie tych możliwości podczas projektu.
Warto zauważyć, że największa obawa przed korzystaniem z rozwiązań chmurowych czyli wyciek danych nie stanowi problemu w przypadku używania SageMath w pracy. Z reguły bowiem treści notatników nie sa poufne. Jedynym zagrożeniem jest utrata danych, która może być praktycznie wyeliminowana poprzez stosowanie systemu kopii zapasowych.
Notatnik oparty na przeglądarce internetowej jest technologią, która jest intensywnie rozwijana w świecie nauki. Najnowocześniejszym rozwiązaniem jest tzw. Jupyter notebook 1. Został on włączony do projektu SageMath i w najnowszych wersjach zastępuje klasyczny notatnik sagenb. W trakcie projektu Jupyter notebook nie oferował jeszcze krytycznych dla realizacji dydaktyki cech takich jak uwspólnianie dokumentów czy ich publikacja. Dlatego projekt został przeprowadzony na poprzednim rozwiązaniu.
- 1
Projekt ma stronę internetową http://jupyter.org
Modele i metody nauczania z wykorzystaniem SageMath¶
Z punktu widzenia aktywności ucznia modele nauczania można podzielić na grupy:
podający (uczeń jest biernym słuchaczem),
podający interaktywny, (uczy myślenia logicznego, wnioskowania),
bezpośredni (uczeń wykonuje ćwiczenia, poznaje algorytmy i procedury, dyskutuje),
poszukujący (twórcze rozwiązywanie problemów),
współpracy z innymi, w tym uczenie innych.
Flipped Classroom (Flipped Teaching) - model odwróconej szkoły (klasy)¶
Odwrócone uczenie, bardzo ogólnie, stanowi zamianę tego, co tradycyjnie przekazywane było uczniom w postaci wykładu oraz dyrektywnych instrukcji, do czasu poza lekcją. Uczniowie w dowolnym czasie (rano, wieczorem, w podróży, itp.) zapoznają się ze wskazanymi przez nauczyciela materiałami multimedialnymi (filmy edukacyjne, nagrane wykłady, prezentacje, podcasty, ebooki, itp.) zamieszczonymi w Internecie, analizują je dyskutując w razie potrzeby z rówieśnikami, a czas lekcyjny poświęca się na dodatkowe wyjaśnienia nauczyciela oraz wykonywanie ćwiczeń pogłębiających wiedzę i utrwalających umiejętności. Uczniowie uczący się szybko mogą w krótszym czasie zgłębić daną wiedzę, z kolei uczniowie pracujący powoli mogą dostosować naukę do swojego tempa (zapoznając się z materiałami w Internecie mogą zatrzymać nauczyciela, cofnąć nagranie, przewinąć je wielokrotnie). Podczas lekcji uczniowie pracują w oparciu o przeanalizowany wcześniej materiał zachęcani przez nauczyciela do myślenia na wyższym poziomie. Czas lekcyjny przy zastosowaniu metody Flipped Teaching można dzięki temu wykorzystać mądrzej i bardziej wartościowo, dopasowując go do indywidualnych potrzeb uczniów. Nauczyciele stosujący metodę wskazują na nietypowy wygląd takich lekcji, podczas których każdy z uczniów pracuje we własnym tempie. Dla obserwatora mogą one stwarzać wrażenie chaosu, choć jest to zamierzone i dla indywidualnych uczniów efektywne. Metoda ta to przykład „blended learningu”, kiedy wiedza teoretyczna dostarczona w postaci e-contentu poprzedza warsztat z trenerem. Podczas stosowania metody Flipped Teaching uczniowie wyposażeni są w narzędzia, umiejętność myślenia, analizowania i przetwarzania informacji oraz rozwiązywania problemów, niezależnie od tego, co w przyszłości będą robić. Metoda ta skutecznie przygotowuje do samodzielności i uczenia się przez całe życie (LLL), zatem jest uniwersalna, niezależnie od przedmiotu na którym jest stosowana.
Metody nauczania¶
W literaturze przedmiotu możemy napotkać wiele sposobów podziału metod nauczania. Dla przykładu Franciszek Szlosek proponuje podział metod nauczania na pięć głównych grup:
Podające: wykład, opis, wyjaśnienia.
Eksponujące: prezentacja, pokaz, demonstracja, film, ekspozycja.
Programowane: z użyciem edukacyjnego programu komputerowego, podręcznika interaktywnego lub programowanych urządzeń dydaktycznych.
Problemowe: wykład problemowy, wykład konwersatoryjny, klasyczna metoda problemowa, symulacje, metody aktywizujące.
Praktyczne: ćwiczenia przedmiotowe, ćwiczenia laboratoryjne, warsztaty, eksperymenty, metoda projektów.
Przykłady zastosowań poszczególnych metod¶
Prezentacja i pokaz możliwości zastosowań SageMath¶
Metody eksponujące w postaci pokazów, prezentacji i demonstracji zostały wykorzystane jako pierwszy kontakt uczniów z aplikacją SageMath. Miały na celu zaciekawienie uczniów, zaintrygowanie ich a także przekonanie, że z SageMath będą w stanie sprawdzić każdą pracę domową z matematyki, czy innego przedmiotu, wymagającą obliczeń czy wykresów.
W XXXIII LO M. Kopernika w Warszawie uczniowie mogli zobaczyć różnorodne możliwości SageMath podczas pierwszych zaplanowanych dla uczniów uczestników projektu Erasmus+ zajęć. Zajęcia trwały jedną godzinę, wybrane do prezentacji zagadnienia w sposób bardzo atrakcyjny pokazywały kolorowe wykresy i animacje, ciekawe problemy rozwiązane z wykorzystaniem narzędzi SageMath - problem “wilki i króliki”, szyfr RSA czy symulacje z fizyki. Ale co najważniejsze, uczniowie mogli ze swoich telefonów komórkowych czy tabletów sprawdzić sami i wykonać polecenia w SageMath.
Na tych zajęciach został także zaprezentowany szkolny serwer SageMath, uczniowie otrzymali konta, omówione zostały kolejne zajęcia a także projekt do samodzielnego wykonania na serwerze SageMath.
Uwaga metodyczna:
Warto zadbać aby uczniowie na początku cyklu zajęć widzieli ich cel w postaci zadania, jakie stawia przed nimi nauczyciel. Równie ważne jest aby uczniowie zobaczyli jakim sposobem ten cel można osiągnąć a także zainteresowali się twórczo nowo poznawanym tematem. Jeśli chodzi o nowe technologie czy narzędzia informatyczne bardzo ważne jest aby nauczyciel zapytał uczniów jakie oni sami mieliby pomysły na zastosowanie i wykorzystanie nowego narzędzia. Uczniowie wówczas mogą się wykazać czasem zaskakującą kreatywnością, czasem bardzo praktycznym podejściem.
Warsztaty - ćwiczenia praktyczne z wykorzystaniem SageMath¶
Warsztaty umożliwiają kształtowanie umiejętności zastosowania wiedzy w praktyce. Polegają przykładowo na rozwiązywaniu zadań, wykonywaniu doświadczeń i eksperymentów, planowaniu i wykonywaniu pomiarów, obliczeń oraz interpretowaniu wyników badań, wykonywaniu symulacji praktycznych i teoretycznych, analizowaniu i praktycznym poznawaniu zjawisk z różnych dziedzin nauki.
Warsztaty służą kształtowaniu umiejętności twórczego wykorzystania wiedzy w praktyce (np. samodzielne poznawanie cech konstrukcji, systemów, procesów, zjawisk), co zmusza ucznia do odkrywania, analizowania, pomysłowości, rozwija naturalną ciekawość, zadawanie pytań i poszukiwanie odpowiedzi.
W XXXIII LO im. M. Kopernika w Warszawie metoda warsztatów została wykorzystana jako kolejne zajęcia po prezentacji możliwości SageMath. Posłużyła do nauki praktycznego wykorzystania i sprawdzenia przez uczniów prezentowanych możliwości. Nauczyciel wybrał najpierw zestaw poleceń do wykonania przez uczniów jednocześnie prezentując na ekranie z rzutnika ich wykonanie. Następnie nauczyciel przedstawił uczniom zestaw zagadnień do samodzielnego wykonania. Takie zajęcia odbywały się zarówno podczas zajęć lekcyjnych jak i pozalekcyjnych dla grupy uczniów uczestników projektu Erasmus+. Zajęcia warsztatowe zostały również przeprowadzone do nauki tworzenia skryptów Python, które były uruchamiane w środowisku SageMath.
Zakres godzinowy i tematyczny zajęć warsztatowych był różnorodny, były prowadzone w wielu grupach. Zajęcia zostały poddane ewaluacji. W ankietach ewaluacyjnych zostały zbadane poszczególne elementy warsztatów: trudność zagadnień, przystępność materiałów dla ucznia, przydatność SageMath z punktu widzenia wykorzystania jego narzędzi do prac domowych, projektów czy przyszłych zastosowań. Uczniowie wypowiadali się także temat sposobu przeprowadzenia zajęć. Wszyscy wypowiedzieli się za tym, aby więcej było zadań do samodzielnego wykonania w grupach.
Uwaga metodyczna:
Podczas warsztatów takie polecenia dla ucznia, które są w formie powtarzania poleceń wykonywanych przez nauczyciela nie mogą trwać długo, ponieważ uczniowie poczują się znudzeni. Takie zajęcia muszą być przeplatane aktywnym zadaniem dla ucznia, wymagającym od niego kreatywności. Uczniowie preferują pracę w grupach podczas warsztatów.
Metoda projektu, projekty grupowe¶
Spośród metod praktycznych stosowanych podczas zajęć szkolnych, na szczególną uwagę zasługuje metoda projektów. Aktywizuje ucznia do kreatywnych poszukiwań i rozwiązywania problemów, uczy współpracy i odpowiedzialności oraz dokumentowania i prezentowania wyników prac. Dlatego warto sięgać po tę metodę na każdym etapie edukacyjnym.
Potrzeby społeczne są niżej w piramidzie potrzeb i dlatego każda praca w grupie angażuje ucznia bardziej niż praca indywidualna, każdej pracy w grupie towarzyszą emocje, a emocje z kolei sprawiają, że uczenie się nabiera innego oblicza, dlatego uczniowie często nie określają swojej pracy w projekcie jako „uczenie się”.
Metoda projektów powstała w latach 20-tych, jako przeciwwaga do nauczania przedmiotowego i systemu klasowo-lekcyjnego Taki system nauczania zrywał z przedmiotowym układem, skupiał naukę z różnych dziedzin w jeden problem do rozwiązania zagadnień np. badawczych i wiązał działalność praktyczną z pracą intelektualną. Twórcą metody projektów był W. H. Kilpatrick, którego ideą było uczenie się przez działanie. Obecnie nauczanie zintegrowane, które jest wykorzystywane w wielu szkołach niepublicznych, nawiązuje do tej metody.
Założeniem metody projektów jest wdrażanie uczniów do twórczego i problemowego myślenia i działania. Pomaga przygotowywać uczniów do rozwiązywania realnych problemów, korzystania z różnorodnych źródeł informacji, pozwala dostrzegać związki pomiędzy różnymi dyscyplinami nauki, pomaga łączyć teorię i praktykę oraz myślenie i działanie - daje możliwość uczenia się za pomocą wielu aktywności.
Metoda projektów stwarza pole do działań ucznia:
rozpoznanie i opis sytuacji problemowej,
formułowanie celów i zadań,
kreatywność, generowanie pomysłów,
integrowanie wiedzy z różnych przedmiotów nauczania,
uruchamianie wyobraźni,
odpowiedzialność, samodzielność,
planowanie zadań, ocena złożoności i trudności zadań,
wytrwałość w poszukiwaniu rozwiązań i realizacji zadań,
samokształcenie,
przygotowanie i prowadzenie publicznych wystąpień,
W zakresie zdobywania informacji:
korzystanie z różnych źródeł informacji,
analizowanie jakości informacji i ocena ich wiarygodności,
klasyfikowanie przydatności informacji z punktu widzenia celów,
wykorzystanie informacji zgodnie z prawem autorskim,
prezentowanie informacji.
Projekty grupowe pozwalają dodatkowo kształtować umiejętności współdziałania:
komunikowania się, (także elektronicznego),
planowania i organizowania własnej pracy i pracy w grupie,
wymiany zasobów, (np. elektronicznej)
wyrażanie własnych opinii i korzystania z opinii wyrażanych przez innych członków grupy,
rozwiązywanie konfliktów.
Założeniem metody projektów jest wdrażanie uczniów do twórczego i problemowego myślenia i działania. Polega na planowaniu i wykonywaniu przez uczniów zadań określonych w ramach projektu (np. w instrukcji do projektu), poprzez samodzielne poszukiwanie i rozwiązywanie problemów pod opieką nauczyciela. Opiera się na praktycznym działaniu: rozpoznawaniu problemów, stawianiu tez i pytań, dowodzeniu, poszukiwaniu odpowiedzi przez obserwacje, badania, analizy, obliczenia, symulacje, eksperymenty czy inne aktywności, np. działania lokalne, społeczne. Uczestnicy realizują temat projektu rozłożony w czasie, pracują samodzielnie lub w zespołach, czy grupach np. klasy, szkoły, z innych szkół czy krajów.
Przygotowanie przez nauczyciela projektu przedmiotowego (lub międzyprzedmiotowego) obejmuje:
wybór zagadnienia do realizacji z wykorzystaniem metody projektów na podstawie analizy efektów kształcenia i ewentualnych możliwości podejmowania działań międzyprzedmiotowych,
przygotowanie instrukcji dla uczniów, zawierającej: określenie celów, metod pracy, terminy realizacji poszczególnych etapów i całości, zadań uczniów, wymagań co do rezultatu pracy, sposobu prezentacji wykonanych zadań i kryteria oceniania,
przygotowanie uczniów do pracy metodą projektów, szczególnie jeśli wcześniej nie wykonywali projektów, omówienie z uczniami zadań i wyników prac,
motywowanie uczniów do zaangażowania się w projekt, podanie przykładów tematów projektów, badań wykonanych przez uczniów, odpowiedzi na pytania problemowe, pokazanie opisów projektów, prezentacji, sprawozdań czy filmów zrealizowanych przez innych uczniów.
wprowadzenie uczniów w wybrane zagadnienie wzbudzenie ich zainteresowania, wskazanie możliwych do rozważenia problemów, przykłady narzędzi, które można użyć do realizacji projektu.
przygotowanie planu doboru grup do realizacji projektów – nauczyciel wybiera sposób podziału na grupy, szczególnie jeśli chciałby zbalansować grupy według wybranego kryterium. Mogą to być:
grupy jednorodne ze względu na wybrane kryterium np. osiągnięcia szkolne, aktywność, umiejętności lub zainteresowania,
grupy o pełnym zróżnicowaniu - każda grupa ma pełny zbiór wg założonego kryterium,
grupy koleżeńskie, chętnie wybierane przez uczniów, ale trudniejsze do zarządzania przez nauczyciela i niekiedy powodujące problemy integracyjne klasy,
grupy doboru celowego lub zadaniowego,
grupy według kolejności na liście klasy,
grupy losowe
Metoda projektów wymaga od nauczyciela wcielenia się w nieco inną rolę. Z osoby dominującej, wyznaczającej tok pracy ucznia oraz głównego źródła informacji (szczególnie jeśli nauczyciel pracuje najczęściej metodami podającymi, mało zostawiając miejsca na aktywność i samodzielność uczniów) - nauczyciel powinien się zmienić w dyskretnego przewodnika, obserwatora i pomocnika. Warto tak zorganizować projekt, aby lwia część prac została wykonana jako praca domowa uczniów i poświęcić np. 15 minut kilku lekcji na pokaz postępów prac. Uczniowie mogą zaplanować wspólne spotkania w szkole, poza szkołą, albo wykorzystać techniki informacyjne i komunikacyjne. Nauczyciel monitoruje postępy realizacji projektu, zgłasza uwagi i doradza.
Z moich obserwacji wynika, że zarówno praca w grupach dwuosobowych, jak i praca w większych grupach jest przez uczniów bardzo chętnie podejmowana. Uczniowie lubią wyzwania, inspirują się wzajemnie, uczą się od siebie, poddają pomysły krytycznej ocenie, w grupie są bardziej aktywni i twórczy. Ale z punktu widzenia nauczyciela praca grupowa uczniów jest trudniejsza do przygotowania i zarządzania, wymaga wnikliwej analizy przy wyborze celów i przemyśleń sposobu ich realizowania.
Wielokrotnie namawiam do współpracy w projekcie międzyprzedmiotowym nauczycieli innych przedmiotów. Dopytuję ich, czy realizują projekty na swoich lekcjach i niestety z przykrością muszę stwierdzić, że nie jest to metoda chętnie wybierana przez nauczycieli. Na pytanie „dlaczego nie?”, odpowiadają najczęściej, że „projekty zabierają wiele godzin, które powinni wykorzystać na realizację materiału” lub, że „projekty niczego nie uczą i na takie zabawy nie mają czasu” albo, że uczniowie znajdują jednego pracowitego ucznia w grupie, który wszystko zrobi a reszta nie robi nic, albo też, że nauczyciel przesuwa termin oddania projektu po raz kolejny, uczniowie się tłumaczą, że część projektu jeszcze nie jest gotowa, ponieważ ktoś był chory albo ma angielski po południu i nie mogli się spotkać. Nauczyciele uważają tę metodę za zbyt pracochłonną i trudną do realizacji. Dlatego niezbyt chętnie sięgają po metodę projektu. Rzeczywiście to niełatwe i wymaga wnikliwych przemyśleń, a sama metoda ma też wady i pułapki, czyhające zarówno na nauczyciela, jak i na uczniów.
Najczęściej podnoszone jest pytanie, czy metodę projektów da się zastosować do skutecznej realizacji obowiązkowego programu nauczania czyli zawartej w nim wiedzy (pojęć, faktów). Szczególnie w kontekście wielu godzin poświęconych na omawianie, wykonywanie i prezentowanie projektów. Wątpliwości budzi także mała skuteczność zdobywania wiedzy przez ucznia na podstawie prezentacji projektów wykonanych przez inne grupy czy innych uczniów.
Ale chyba największy problem jest taki, że duża część nauczycieli jest przywiązana do tradycyjnych metod nauczania i rzadziej wybiera metody aktywne podczas zajęć.
Na obronę metody projektów należy podkreślić, że większości zagrożeń da się uniknąć, jeśli się je zna.
W XXX III LO im. M. Kopernika w Warszawie metoda projektu została wykorzystana podczas zajęć informatyki. Projekty zostały wykonane w trzech grupach uczniów z klasy drugiej, tematem projektu było badanie funkcji.
Zaprezentowane zostały materiały w postaci instrukcji do projektu, opisu przeprowadzonych zajęć i przykładowych prac uczniów. Ponadto realizacja projektu w trzech grupach została zaplanowana tak, aby posłużyła do wykonania badań ewaluacyjnych porównujących wykorzystane metody. To badanie pokazało, że projekt został bardzo dobrze oceniony przez uczniów, uznali, że dużo się nauczyli przydatnych rzeczy i była to dla nich twórcze zadanie.
Uwaga metodyczna:
SageMath ma bardzo bogate możliwości, które mogą posłużyć nauczycielowi do zaplanowania zadań o szerszym charakterze, niż pojedyncza lekcja czy cykl lekcji. Można zaplanować długoterminowe prace o charakterze problemowym, kiedy uczniowie sami dochodzą do zbadania lub udowodnienia teorii, praw czy zasad. Sformułowane problemy, pytania, zagadnienia, łącznie z poznaniem teorii można zlecić uczniom jako tematy do odwróconych lekcji czy prac grupowych lub projektów indywidualnych. Ponadto w oddziałach, w których uczniowie znają język Python można zaplanować zagadnienia wymagające napisania skryptów, które pozwolą na realizację zaplanowanego algorytmu do rozwiązania problemu. W ten sposób można zrealizować wiele celów zarówno dotyczących realizacji materiału jak i dać uczniom okazję do kreatywności. Warto nabywać doświadczeń i w każdym kolejnym projekcie eliminować napotkane problemy. Zaś zdobywane przez ucznia umiejętności podczas pracy metodą projektów są ogromnie istotne w procesie nauczania jako całości.
Podsumowanie tego rozdziału¶
Nasze doświadczenia pokazują, że znajomość możliwości SageMath pozwala na zorganizowanie ciekawych zajęć zarówno lekcyjnych, jak i pozalekcyjnych, w formie warsztatów, pracy problemowej, w formie odwróconej lekcji czy projektów przedmiotowych, międzyprzedmiotowych, indywidualnych i grupowych. Jeśli nauczyciel chciałby urozmaicać metody dydaktyczne, sięgać po nowe technologie oparte na doświadczeniach innych nauczycieli aby stale rozwijać zainteresowania uczniów - z pewnością znajdzie w proponowanej metodyce i przygotowanych materiałach (rezultatach naszego projektu) cenne inspiracje wzbogacające jego warsztat pracy.