Optimisation problem in analytical geometry

Problem

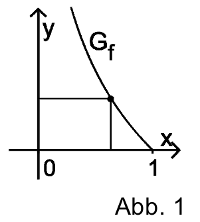
Consider all rectangles in a coordinate system (cf. figure 1) which fulfill the following conditions:

1. Two sides lie on the coordinate axes.

2. One vertex lies on the graph \(G_f\) of the function \(f : x\mapsto -\ln x\) with \(0<x<1\).

Figure 1 depicts such a rectangle.

Among the considered rectangles there exist one with the largest area. Calculate the side lengths of this rectangle.

Solution

The area of the considered rectangles is obtained as product of height and width. The width is given by the \(x\)-value of the vertex lying on the function’s graph. The height corresponds to its \(y\)-value, i.e. \(f(x)\). The area of a rectangle with a given value for \(x\) is therefore obtained as

\[A(x)=xf(x)=-x\ln(x).\]

In order to determine the the rectangle with the biggest area, we need to find the extremum of \(A(x)\) which is obtained from

\[A'(x_0)=-\ln(x_0)-1 = 0.\]

Because of \(A''(x)=-1/x <0\) this extremum is always a maximum. It lies at \(x_0=1/\mathrm{e}\) with \(f(x_0)=1\). The corresponding rectangle therefore has a width of \(1/\mathrm{e}\), a height of \(1\) and circumscribes an area \(1/\mathrm{e}\).

We can determine the rectangle with maximum area also with the help of Sage by asking for a zero of the derivative of the area.

The following two figures show the rectangle under the graph \(G_f\) on the left and the corresponding area as a green point in the right figure as a function of the variable width \(x_0\).