6. Instrumenty stałego dochodu

6.1. Depozyt na rynku pieniężnym

Depozyty rynku pieniężnego to instrumenty stałego oprocentowania, które to kontrakty są zawierane na określony okres czasu i nie mogą być likwidowane przed terminem zapadalności.

Ponieważ są instrumentami rynku pieniężnego ich okres do zapadalności jest mniejszy od jednego roku. Powoduje to potrzebę przeliczania rocznej stopy procentownia na okresy mniejsze od roku. Sumę odsetek na koniec okresu depozytu wyliczyc można ze wzoru:

\[R = D d \frac{n}{360}\]

Gdzie:

• R = suma odsetek

• D = wartość depozytu

• d = oprocentowanie depozytu (annualizowane)

• n = ilość dni pomiędzy początkiem okresu depozytu a jego zapadalnością

Należy zwrócić uwagę, że przyjęto tutaj standard roku liczącego 360 dni. Gdyby standard był inny (a jest to częsty przypadek) należy uwzględniać inną wartość dni w roku. Efektywną stopę zwrotu na depozycie można wyliczyć ze wzoru na wartość pieniądza w czasie.

6.2. Instrumenty dyskontowe

Są to typowe instrumenty rynku pieniężnego wyceniane na zasadzie dyskonta tzn. są handlowane z dyskontem w stosunku do wartości nominalnej. Jak już to było wykazane, ich cena aktualna jest równa

\[P =\frac{FV}{(1+Y \frac{DDW}{360})}\]

gdzie:

• P - cena rynkowa

• FV - wartość nominalna

• Y - rentowność

• DDW - ilość dni do wykupu,

Przyjęto standard roku liczącego 360 dni- standard dla Bonów Skarbowych na polskim rynku.

6.3. Wycena obligacji

Obligacja jest to papier wartościowy (instrument finansowy), stwierdzający zaciągnięcie przez emitenta obligacji długu wobec posiadacza obligacji - zwanego obligatariuszem i zawierający zobowiązanie, wobec obligatariusza do wykupu obligacji - jako zwrotu zaciągniętego długu oraz wypłacenia odsetek za korzystanie z użyczonych pieniędzy oraz terminowość wypłat. Odsetki mogą być wypłacane w określonych momentach (tzw. kupony) lub w postaci dyskonta w momencie emisji (obligacja zerokuponowa). Innymi słowy jest to dokument potwierdzający zaciągnięcie długu i zobowiązanie do jego spłacenia.

Dlaczego emitent wybrał taki sposób pozyskania kapitałów na finansowanie swych projektów? Dlaczego nie zaciągnął kredytu bankowego? Pytania te wskazują na podstawowe różnice w sposobie finansowania przy pomocy rynku kapitałowego a rynku usług bankowych.

Pierwsza różnica uniknięcia pośrednictwa banków wykorzystując obszar marży bankowej dla korzyści uczestników rynku. Banki oferują depozyty dla klientów (płacąc im w zamian odsetki) by mieć środki na udzielanie kredytów. Marża banku to różnica oprocentowania między oprocentowaniem depozytów a oprocentowaniem kredytów. Emitent obligacji chce uzyskać niższe oprocentowane kredytu oferując dla uczestników rynku wyższe oprocentowanie niż oprocentowanie depozytów bankowych (szansa dla obligatariuszy) ale uzyskując dla siebie niższe oprocentowanie niż w przypadku oprocentowania kredytów bankowych (korzyść emitenta).

Druga różnica wiąże się kształtem strumieni przepływów środków pieniężnych w obu przypadkach. Typowy kredyt polega na początkowym transferze kapitału od banku do kredytobiorcy i kolejnych regularnych (najczęściej) spłatach części kapitału wraz z odsetkami od niezwróconego do tego momentu kapitału. W przypadku obligacji (najczęściej) w chwili początkowej następuje przepływ środków od obligatoriusza do emitenta, następnie w równych czasowych okresach emitent płaci odsetki od pożyczonego kapitału. Wraz ze spłatą ostatniej kwoty odsetek emitent spłaca całą kwotę, którą jest dłużny obligatariuszom.

Trzecia różnica to korzyść z tego, że obligacja jest papierem wartościowym będącym w obrocie. Właściciel obligacji, jeśli potrzebuje gotówki nie musi czekać na spłatę przez emitenta ale może uzyskać środki pieniężne sprzedając obligacje na rynku komuś innemu.

Cechy charakterystyczne określające obligacje:

• wartość nominalna - jest to wartość zaciągniętego długu, od której nalicza się odsetki i która jest płacona w momencie wykupu przez emitenta posiadaczowi obligacji;

• termin wykupu - jest to termin, w którym obligatariusz otrzymuje od emitenta kwotę równą wartości nominalnej; w terminie wykupu obligacja podlega wykupowi;

• oprocentowanie - stopa procentowa określająca wielkość odsetek wypłaconych obligatariuszowi;

• terminy płacenia odsetek, - czyli częstotliwość wypłat odsetek. Przykładowo: raz na rok, raz na pól roku, kwartalnie.

• cena emisyjna - to cena, po której obligacja jest sprzedawana jej pierwszemu posiadaczowi w momencie emisji. Cena ta może być zarówno niższa jak i wyższa od ceny nominalnej. Decyzja emitenta zależy w tym przypadku do przewidywanego zainteresowania i oprocentowania obligacji.

W charakterystycznych cechach obligacji wymienione zostały dwie cechy związana z wartością obligacją. Były to cena (wartość) nominalna i cena emisyjna. W rynkowym obrocie obligacjami używa się jeszcze terminów ceny rynkowej i rozliczeniowej. «»Cena rynkowa»» (kurs giełdowy), jest ustalana na codziennych sesjach giełdowych, jako wypadkowa popytu i podaży. Oczywiście dotyczy to obligacji dopuszczonych do obrotu publicznego i notowanych na giełdzie. Określana jest w procentach wartości nominalnej. Nie jest to jednak faktycznie ta cena, jaką faktycznie płaci kupujący i otrzymuje sprzedający obligacje, ponieważ nie uwzględnia narosłych odsetek przypadających w danym dniu. «»Cena rozliczeniowa»», czyli cena giełdowa powiększona o narosłe odsetki, to rzeczywista kwota transakcyjna, jaką płaci kupujący i otrzymuje sprzedający obligacje. Aby ją obliczyć, należy po prostu dodać do ceny rynkowej należne w tym dniu odsetki. Wartość obligacji na rynku (a zatem jej cena), jak zostało wcześniej wspomniane, kształtuje się w wyniku popytu i podaży, które z kolei zależą od różnych czynników. Najważniejszym czynnikiem kształtującym wartość obligacji jest poziom stóp procentowych.

Inwestorzy często dokonują wyceny obligacji. Wycena obligacji polega na określaniu tzw. „godziwej ceny obligacji” (fair price), która powinna odzwierciedlać wartość obligacji. Najczęściej stosowaną metodą przy wycenie jest metoda dochodowa, inaczej zwana metodą zdyskontowanych przepływów pieniężnych.

Wycena obligacji - polecana literatura poszerzająca, objaśniająca ten rozdział to: Joanna Place- „Basic Bond Analysis”- Handbook in Central banking- nr.20- Bank of England,2000; raz pozycja autorstwa Jerzego Dzieży - «Instrumenty stałego dochodu- AGH- dostepne w sieci Internet, oraz David Blake - Financial Market Analysis- McGraw- Hill.

6.4. Cena godziwa (fair price)

Aktywo , jakim jest obligacja, generuje zdefiniowane strumienie pieniężne w czasie. Inwestor kupuje te strumienie oceniając ich wartość dla siebie. Jeśli mamy obligację, której emitent zobowiązuje się do płacenia odsetek regularnie raz do roku i zamierza zwrócić zaciągnięte zobowiązanie (wartość nominalną) w chwili wykupu, na koniec życia zobowiązania, to godziwa cena dla inwestora takiego instrumentu jest wynikiem zdyskontowanej wartości bieżącej przepływów pieniężnych generowanych przez takie zobowiązanie. Stopa dyskontowa jest określana przez rynek.

\[P_o=\sum\limits_{i=1}^n\frac{C}{(1+r)^i} +\frac{P_N}{(1+r)^n},\]

gdzie

• \(C\) - odsetki (ang. coupon)

• \(P_o\) - wartość obligacji

• \(P_n\) - wartość nominalna

• \(r\) - stopa dyskontowa

Przykład (obligacja ze stałym kuponem)

Jaka jest wartość obligacji o terminie wykupu przypadającym za dwa lata. Wartość nominalna tej obligacji wynosi 100, oprocentowanie 6%, odsetki płacone są, co rok. Wymagana stopa dochodu określona przez inwestora wynosi 7% w skali roku.

Po podstawieniu do wzoru otrzymujemy:

\(\ P_o=\frac{6}{(1+0,07)^1} +\frac{106}{(1+0,07)^2}.\)

W naszym przypadku:

\(C=0,06x100 = 0,06\)

\(R = 7\% = 0,07.\)

Wartość nominalna wynosi 100 czyli w 2 roku nastąpi wpływ \(\frac{100+6}{(1+0,07)^2}\)

Dla naszego inwestora wartość tej obligacji wynosi 98, 2 jednostek pieniężnych.

6.5. Cena godziwa dla obligacji wieczystych

Obligacje wieczyste zwane konsolami nie są nigdy wykupywane, a ich posiadacz otrzymuje nieskończony strumień odsetek, zwany rentą wieczystą. W tym przypadku \(n\to\infty\).

Więc cena godziwa:

\[P_o = \frac {C}{r}\]

jest to sumą szeregu geometrycznego.

6.6. Obligacja zerokuponowa

Obligacje zerokuponowe to typowe instrumenty dyskontowe. Ich cena jest wyznaczana poprzez dyskontowanie ich wartości nominalnej do dnia wyceny. Wzór stosowany dotychczas do wyceny obligacji przybierze postać:

\[P_o=\sum\limits_{i=1}^n\frac{C}{(1+r)^i} +\frac{P_N}{(1+r)^n}= \sum\limits_{i=1}^n\frac{0}{(1+r)^i} +\frac{P_N}{(1+r)^n}\ = \frac{P_N}{(1+r)^n}\]

Podany wyżej wzór dotyczy obligacji wypłacającej kupon jeden raz na rok. Dla większej ilości okresów odsetkowych aby obliczyć wartość obligacji należy zdyskontować strumienie pieniężne, jakie generuje do czasu wykupu.

Jej wartość można wyrazić następująco:

\[P_o=\sum\limits_{i=1}^n\frac{C_i/m}{(1+r/m)^i} +\frac{P_N}{(1+r/m)^n}\]

Gdzie:

• \(m\) - liczba płatności odsetkowych w roku

• \(n\) - to liczba okresów odsetkowych w roku, \(n=mT\)

• \(T\) - długość życia obligacji w latach

• \(P_n\) - wartość nominalna obligacji.

• \(C_i\) - wysokość kuponu w i-tym okresie odsetkowym.

• \(i\) - i-ty okres odsetkowy (i zawiera się między 1 a n) - \(r\) - stopa dyskontowa.

6.7. Wycena przy kapitalizacji ciągłej

Powyższe wyliczenia dotyczą kapitalizacji dyskretnej obligacji . Dla ciągłego procesu kapitalizacji i stałego kuponu wartość obligacji będzie opisywana zależnością:

\[P_o=\sum\limits_{i=1}^n {(C/m)}{e^{-r t_i}} +\ {P_N}{e^{-rt_n}},\]

gdzie:

• \(t_i\) - moment wypłaty i-tego kuponu

pozostałe oznaczenia jak wyżej.

6.8. Rentowność obligacji

Obligacja jest instrumentem dłużnym. Jeśli inwestor zainwestował pieniądze w czyjś dług spodziewa się nagrody za czas, w którym jego pieniędzmi dysponuje ktoś inny. Oczywiście w przypadku obligacji inwestor oprócz kwoty nominalnej pożyczki, której zwrot następuje po zakończeniu życia zobowiązania, dostaje regularnie wypłacane, co okres odsetki. Ale obligacja może zmienić właściciela miedzy okresami wypłaty kuponu. Każdy z posiadaczy tej obligacji rości sobie prawo do partycypacji w tym kuponie, gdyż każdy z inwestorów przez określoną ilość dni finansuje dług. Każdy z nich chce udziału w kuponie proporcjonalnie do czasu, w jakim był posiadaczem obligacji w okresie miedzy wypłatą kuponu. Cena rozliczeniowa obligacji to pewna wartość zwana ceną czystą obligacji plus należne odsetki za okres posiadania. Zależność jest liniowa.

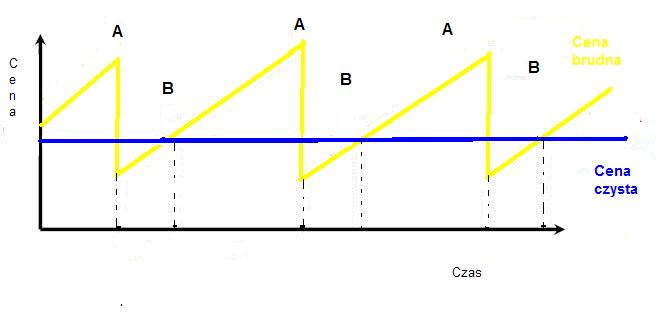
Tak zdefiniowana cena nazywa się cena „brudna” i po takiej cenie rozliczają się tak naprawdę uczestnicy rynku. Cena brudna, a właściwie jej zachowanie w czasie posiada kształt przypominający zęby piły.

Dodatkowo należy wspomnieć o następującej sytuacji. Kupon jest wypłacany właścicielowi obligacji. Właścicielowi, w dniu naliczania kuponu. Jeśli miedzy dniem naliczenia kuponu a dniem wypłacenia fizycznego pieniędzy obligacja zmieni właściciela to nowy można powiedzieć, że stary właściciel dostaje pieniądze za czas, kiedy obligacja do niego nie należy. W takiej sytuacji nowy właściciel jest „wynagradzany” przez starego właściciela tym, że cena brudna w tym czasie jest niższa od ceny czystej. Rysunek obok modelowo obrazuje taką sytuację i zachowanie się w czasie cen obligacji.

Zgodnie z (David Blake - Fin. Mark. Analysis), dla roku o 365 dniach, narosłe odsetki są równe:

\[A_i =d\frac{{N_a}-{N_b}}{365},\]

Gdzie :

• \(Ai\) - należne odsetki

• \(N_a\) - ilość dni miedzy dniem naliczenia odsetek i datą wypłaty kuponu

• \(N_b\) - liczba dni miedzy data naliczenia kuponu a dniem transakcji

• \(d\) - wartość płatności kuponu

6.9. Stopa zwrotu z obligacji

Ze względu na często skomplikowane strumienie pieniężne, jakie generują obligacje, trudne jest je (obligacje) porównywać na podstawie ceny, raczej robi się to poprzez porównywania stopy zwrotu. Istnieje kilka różnych stóp zwrotu.

6.9.1. Stopa bieżąca

Najprostszym sposobem oceny obligacji jest określenie stopy bieżącej.

Jest ona definiowana, jako stosunek kuponu, czyli oprocentowania obligacji w skali roku do ceny czystej:

\[r_c=\frac{d}{P},\]

gdzie:

• \(r_c\) - bieżąca stopa

• \(P\) - cena czysta

• \(d\) - oprocentowanie obligacji w skali roku

Właściwszym byłoby, w zasadzie używać ceny brudnej do takiej oceny, gdyż właściwie taką cenę płaci się za obligacje. Jednakże należy pamiętać o jej podobieństwie do piły i stopa bieżąca też miałby taki charakter.

6.9.2. Stopa zwrotu w terminie do wykupu (Yield to maturity)

Do tego momentu mówiąc o cenie obligacji używano wzoru:

\[P_o=\sum\limits_{i=1}^n\frac{C_i/m}{(1+r/m)^i} +\frac{P_N}{(1+r/m)^n}\]

Wyceniając ciąg płatności zakładaliśmy wartość stopy dyskontowej.

Na rynku mamy sytuacje nieco inną, znamy raczej bieżące ceny rynkowe obligacji. Aby wiec wycenić jej stopę zwrotu, czyli stopę od chwili nabycia do końca życia instrumentu, powinno się za stronę lewą równania wstawić wartość rynkowa obligacji i wyliczyć stopę zwrotu.

Tak wyliczona stopa zwrotu to jest nic innego niż wewnętrzna stopa zwrotu (IRR) z inwestycji.

Stopa zwrotu w terminie do dnia wykupu (YTM) liczona przy założeniu reinwestowania kuponów po rentowności YTM.

Stopę tą wylicza się rozwiązując powyższe równanie względem \(r\).

Łatwiej jest napisać „rozwiązując” niż to zrobić. Nie znamy analitycznej postaci rozwiązania - stosuje się w tym przypadku metody przybliżone.

6.10. Interpretacja koncepcji stopy zwrotu w terminie do wykupu

Takie zdefiniowanie powyższej wielkości ma szereg implikacji i wskazuje na wiele istotnych aspektów.

Po pierwsze stopa zwrotu do wykupu to metoda określenia ceny obligacji. Mając ceną rynkową potrafimy (bardziej lub mniej dokładnie) wyliczyć stopę zwrotu i odwrotnie, (co łatwiejsze) mając stopę YTM można wyznaczyć cenę obligacji.

Druga interpretacja to taka, że YTM odpowiada „ekwiwalentnej” stopie procentowej depozytu bankowego. Tzn. że gdyby zdeponować środki na depozycie bankowym oprocentowanym stopą YTM to zachowywać się będzie jak inwestycja w obligacje (i odwrotnie).

Ta analogia ekwiwalentu stopy depozytowej stwarza możliwość używania YTM, jako sposobu porównywania rożnych obligacji o różnych kuponach, czasie życia i różnych cenach rynkowych.

Innymi słowy, przykładowo, daje to inwestorowi łatwy wybór czy ma zainwestować, w które konto czy oprocentowane np. na 6% czy na 5,5% (oba porównywalnie, co do ryzyka i sposobu naliczania procentu). Jeśli stanie przed takim wyborem z pewnością wybierze konto wyżej oprocentowane.

W przypadku stopy oprocentowania rachunku, która jest jedyną miarą inwestycji, w przypadku YTM nie można powiedzieć, że jest to jedyna i ostateczna wielkość pomiaru wartości inwestycji. W kontekście porównania do rachunku bankowego należy wskazać trzy zasadnicze miejsca gdzie analogia załamuje się (S. Homer i L. Leibowitz-„Inside yield book”-PRENTICE -HALL, Inc & N.Y Insitute of Finance).

Pierwszy punkt to, to, że inwestor sam dowolnie decyduje o wypłatach ze swojego konta, (co do wielkości i terminów). Tak nie jest w przypadku obligacji, którą inwestor nabywa wraz ze specyficzną dla niej realizacją kuponu i datą zapadalności. Ponadto inwestor działa w ramach swoich potrzeb finansowania i pod względem czasu, wielkości i kierunku przepływów środków. W związku z tym nawet mając do wyboru dwie obligacje o tym samym YTM, ale generujących różne czasowo przepływy, wybierze tą, której właśnie przepływy będą bardziej mu odpowiadały.

Szukanie podobieństwa zawodzi w przypadku stałości oprocentowania rachunku bankowego. Inwestor nie martwi się o poziom przyszłych stóp procentowych, bo ma je ustalone. Nie jest tak w przypadku obligacji, gdy wpływy z kuponów są inwestowane na bieżąco w dostępne rynkowo instrumenty, których stopa zwrotu nie musi być równa stopie YTM pierwszego instrumentu.

Dalej, ciągnąc tę myśl, jest to, że wypłata nominału jest związaną z datą zapadalności. Różnica występuje, gdy właściciel nominału zainwestowane chce go wyciągać przed data zapadalności. Właściciel konta bankowego zna wielkość nominału depozytu w każdym czasie bez względu na poziom stóp procentowych. W przypadku obligacji jedyne, co może zrobić to sprzedać obligacje po cenach rynkowych. Inwestor w obligacje wie jedynie, że rynek obligacji stwarza możliwości i ryzyka związane z jego kapitałem w czasie do zapadalności.

Należy jeszcze zwrócić uwagę na jeden aspekt. YTM, jako stopa procentowa w określeniu wartości przyszłej, dzisiejszej inwestycji. W tym miejscu często popełniane są błędy. W określeniu wartości przyszłej stopa procentowa jest stopą, po której zostanie zainwestowany (reinwestowany) kupon w chwili, kiedy stanie się dostępny. Mimo podobnej konstrukcji matematycznej, YTM nie jest prognozą stopy reinwestycji i nie może (chyba, że przypadkowo) reprezentować stopy wzrostu wartości przyszłej. Tak naprawdę może reprezentować tę stopę tylko wtedy, gdy reinwestycje nastąpią ze stopą równa stopie YTM.

Stopa YTM jest stopą określoną w danym dniu dla danej ceny. Jest niezwykle pomocnym instrumentem przy podejmowaniu decyzji, ale nie jedynym parametrem uzasadniającym decyzje inwestycyjne.

6.11. Ryzyko stopy procentowej

6.11.1. Ryzyka inwestycji w obligacje

Ryzyko inwestycji w obligacji wiążę się z kilkoma jego źródłami.

Ryzyko wiąże się, bowiem, z:

• Możliwością niedotrzymania umowy przez emitenta (ryzyko bilansu)(default risk)

• Zmianami cen obligacji na rynku związanymi ze zmianą stóp procentowych.

Pierwsze ryzyko można poznać albo przez dokładna analizę sytuacji finansowej emitenta wykonaną osobiście albo korzystając z ocen agencji ratingowej. Wykonanie analizy pozwala na dokonanie oceny ryzyka, ale nie usuwa jego istnienia.

Ryzyko drugie, czyli ryzyko zmian stóp procentowych wiążę się z obiektywnie istniejącymi na rynku pieniężnym zmianami cen instrumentów. Rynek finansowy podlega szeregowi wpływów a ceny obligacji, podobnie jak każdego instrumentu wycenianego przez rynek, reagują na każdą istotną informację gospodarczą. Nawet intuicyjnie widać, że ryzyko zmiany stóp procentowych dla obligacji jest większe im dłuższy jest czas życia tego instrumentu. Różne rodzaje obligacji są narażone na tego typu ryzyko w różnym stopniu. Najbardziej wrażliwe są ceny obligacji o stałym oprocentowaniu oraz obligacje o najdłuższych terminach do wykupu. Ryzyko wiąże się z niepewnością, co do wielkości dochodu z obligacji w przyszłości, jak i możliwością niekorzystnej zmiany ich ceny. Ceny obligacji o stałym oprocentowaniu (w tym zerokuponowych) spadają, gdy rosną oficjalne i rynkowe stopy procentowe. Przy spadających stopach procentowych rosnąć będą ceny tych obligacji, ale także tych o zmiennym oprocentowaniu, które zapewniają odsetki wyższe niż nowo emitowane papiery.

Przykład

Aby zilustrować mechanizm zmiany ceny obligacji przy zmianie stóp procentowych zanalizujmy poniższy przykład: Inwestor zakupił 10 letnią obligację oprocentowaną na 8% rocznie. Oznacza to tyle, że przez najbliższe 10 lat będzie otrzymywał roczne odsetki w wysokości 8 zł. To gwarantuje mu zakupiona obligacja, bez względu na poziom stóp procentowych na rynku. Niech wartość nominalna obligacji wynosi 100 PLN. Jednakże stopy procentowe zostały np. decyzją Rady Polityki Pieniężnej, podniesione. Zaraz po tej decyzji emitent wypuścił nową obligację oprocentowaną na 10% rocznie. Inwestor widzi, że jego inwestycja nie jest tak dobra jak byłaby nowa inwestycja w nową obligacje. Rozsądnie postępując powinien on sprzedać „starą” obligację i kupić nową, bardziej dochodową.

Ale jak sprzedać starą nisko oprocentowaną, gdy na rynku dostępne są obligacje o wyższej rentowności? Aby sprzedać Inwestor musi obniżyć cenę posiadanej obligacji tak by nowa cena kompensowała nabywcy niższe odsetki. Jest to możliwe, gdy zaoferuje posiadaną obligację (o wartości nominalnej 100PLN) za 80 PLN. Przy takiej cenie nowy inwestor widzi, że może kupić albo „starą „ obligację za 80 PLN od Inwestora i przynoszącą 8 PLN rocznie, (czyli 10%) albo nową obligację z rynku o wartości 100 zł przynoszący 10 zł zysku. W każdym przypadku zarobi 10 procent. Czyli, przy takiej cenie obligacji może brać pod uwagę propozycje sprzedaży Inwestora.

Inwestor doznał konsekwencji efektu ryzyka zmiany stopy procentowej i przy jej wzroście poniósł stratę na swojej inwestycji. Ryzyko inwestycji w obligacje istnieje mimo, że uważane są za instrumenty finansowe należące do grupy bezpiecznych.

Zastanawiając się nad tym ryzykiem popatrzmy na trzy obligacje zero kuponowe. Roczną, 2-letnią i 10-letnią obligacje zerokuponową. Wartość nominalna P=1,000 jednostek pieniężnych. Roczna stopa R=10%,.Policzmy zmianę stopy procentowej i cenę obligacji przy zmianie oprocentowania o 1%. Otrzymamy następującą tabelę wiążącą zmiany stopy procentowej i cenę obligacji biorąc pod uwagę zmiany o 1%:

Związek między ceną obligacji a jej rentownością pokazuje krzywa na rysunku:

Jej zamieszczenie ma na celu pokazanie, że związek miedzy ceną a rentownością nie jest liniowy, gdyż, aby podać jej cenę należy wyliczyć jej \(P_o\) czyli wartość aktualną ze wzoru przytaczanego wcześniej gdzie stopa procentowa występuje w mianowniku ułamka dyskontującego. Kształt tej krzywej jest różny dla różnego czasu życia obligacji (w wyliczeniach należy wtedy brać pod uwagę więcej okresów kuponowych, czyli sumować więcej wyrazów, w których stopa procentowa występować będzie w wyższych potęgach). Innymi słowy obligacje o długim okresie zapadalności mają bardziej stromą krzywą rentowność/ cena niż obligacje o krótkim okresie życia. Zatem są bardziej wrażliwe na zmiany rynkowych stóp procentowych niż te o krótszym życiu . Zatem czas do zapadalności nie jest najlepszą miarą wrażliwości obligacji. W tym miejscu można zadać jeszcze jedno pytanie czy zmiana stopy o +1% ma taki sam wpływ na cenę jak o jak o-1%?

Aby ocenić ryzyko zmiany stóp procentowych w przypadku obligacji można użyć kilku metod.

Informacja

Bardzo ciekawe opracowanie zawiera link http://home.agh.edu.pl/~dzieza/fixed_income/tp_not_agh.pdf. Opracowanie to było inspirujące również przy pisaniu niniejszego tekstu.

Jak powinien wyglądać sposób na pomiar ryzyka obligacji?

Zmiana ceny obligacji posiada pewne cechy, które należy brać pod uwagę myśląc o ryzyku stopy procentowej.

• Ceny obligacji zmieniają odwrotnie do zmian stóp procentowych. (nie jest to zależność liniowa).

• Jeśli wszystkie inne czynniki są stałe ryzyko stopy procentowej obligacji rośnie z długością czasu do zapadalności . (Zmienność cen obligacji i czas do zapadalności są z sobą związane. )

• Zmiana ceny będąca skutkiem równego wzrostu/zmalenia rentowności (YTM) obligacji jest asymetryczna.

• Czas życia obligacji (czas do zapadalności ) nie jest najlepszą miarą ryzyka. Jak widać bowiem im dłuższy czas do zapadalności tym więcej strumieni płatności generuje obligacja i wzór na jej wartość staje się wielomianem coraz to wyższego rządu.

O ile zmienność ceny obligacji zmienia się odwrotnie do jej kuponu i zgodnie z jej czasem do zapadalności, staje się koniecznym zdefiniowanie kombinacji obu czynników by móc lepiej zapanować nad ryzykiem ceny. Potrzebna jest taką wielkość kompozytowa, uwzględniająca zarówno kupon jak i zapadalność.

Porównując przepływy pieniężne generowane przez obligacje widać, że dla różnych obligacji strumienie te różnią się długością czasu generowania jak i wielkością kuponu obligacji, czyli co za ty idzie ich wartością bieżącą (wynikającą z wartości pieniądza w czasie). Należy więc skonstruować wielkość pozwalającą na porównywanie tych strumieni.

W tym celu wprowadzono średni, ważony pieniędzmi (kapitałem) czas do zapadalności. Wielkość taką nazywa się „duration”.

6.11.2. Duration

Ze względu na efekt ważenia będzie to moment czasu przypadający między pierwszą a ostatnią płatnością. Obligacja kuponowa będzie miała duration krótsze od czasu do zapadalności.

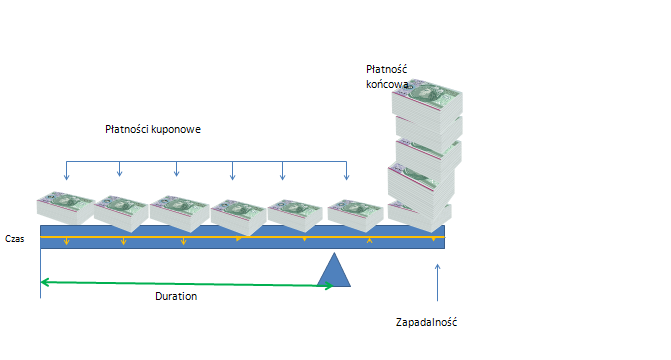
Dla obligacji zero kuponowej jest on równy czasowi życia czyli czasowi do zapadalności.

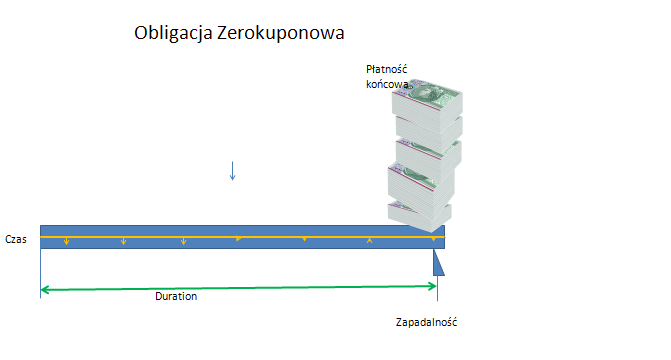
Zamieszczone tu dwa obrazki maja służyć ilustracji sensu „ duration” jako punktu równowagi strumieni pieniężnych generowanych przez obligacje. Ilustracja ta jednak nie pokazuje znanego dobrze efektu zmiany wartości pieniądza w czasie.

Dyskontując płatności generowane przez obligacje widzimy, że wartość aktualna (present) tych przepływów zachowuje się podobnie do schematu przedstawionego na rysunku. Ostatnie płatność to kupon wraz z nominałem. Duration (\(D\)) instrumentu o stałym dochodzie możemy zdefiniować, jako średnią ważoną chwil czasowych, w których dokonywane są płatności gotówkowe. Wagami są wartości aktualne (present) poszczególnych przepływów gotówkowych. Przypuśćmy, że przepływy gotówkowe otrzymywane są w chwilach \(t1, t2, . . ., t_n\). Wtedy duration takiego strumienia płatności dane jest następująco:

\[D=\frac{PV(t_1)t_1+PV(t_2)t_2 + … PV(t_N)t_N}{P_o}\]

Gdzie:

• \(P_o\) to wartość aktualna strumienia płatności czyli wartość obligacji

• \(PV(t_i)\) - to wartość aktualna i- tej płatności kuponu w chwili \(t_i\)

Ilustracją idei tych wyliczeń jest rysunek poniżej. Ilustruje on sens duration.

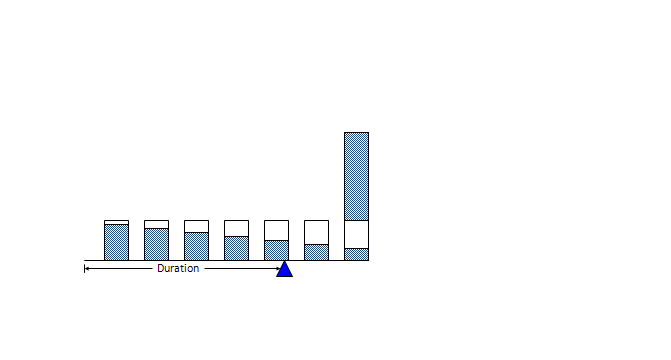
Podsumowując:

Tak zdefiniowane duration (\(D\)) to średnia czasu wpłat ważonych ich wielkością. Duration obligacji kuponowej jest zawsze mniejsza niż jej okres do zapadalności ponieważ pośrednie płatności są ważone.

Duration dla obligacji zerokuponowej jest równy jej okresowi do zapadalności.

• Widać negatywną relacje między duration a kuponem.

• Widać dodatnią relacje między czasem do zapadalności i duration.

• Widać odwrotną zależność miedzy YTM i duration.

6.11.3. Duration według Macaulay’a - Duration obligacji przy kapitalizacji dyskretnej

Cena obligacji jako aktualna wartość płatności generowanych przez obligacje opisana jest wzorem:

\[P_o = \sum\limits_{i=1}^n\frac{C_i/m}{(1+r/m)^i} +\frac{P_N}{(1+r/m)^n}\]

Jeśli policzymy pierwszą pochodną ceny względem stopy to otrzymamy:

\[\frac{dp}{dr} = \sum\limits_{i=1}^n\frac{(-i/m)C_i/m}{(1+r/m)^i+1} +\frac{P_N}{(1+r/m)^n+1}\]

Wyłączając czynnik \(\frac{1}{1+y/m}\) przed nawias a następnie dzieląc obie strony przez cenę obligacji możemy przekształcić wzór do postaci:

\[\frac{dp}{dr}1/P=\sum\limits_{i=1}^n\frac{(-i/m)C/m}{(1+r/m)^i} 1/P+\frac{P_N}{(1+r/m)^n}1/P\]

Patrząc na wyrażenie po prawej stronie równania widać, że jest to nic inne jak Duration \(D\) zdefiniowana już poprzednio jako średni ważony okres do zapadalności.

Czyli, z dokładnością do znaku,

\[\frac{dp}{dr}\frac{1}{P}=-D\frac{1}{1+r}\]

Lewa strona równania określa elastyczność ceny względem zmiany stopy procentowej. Duration ilustruje stromość, nachylenie krzywej w punkcie \(r\). Oznacza to, że aktywa o takiej samej duration są tak samo czułe na zmianę stopy procentowej.

Poeksperymentuj z duration!

Możemy wykonać obliczenia Duration dla pewnej obligacji z FV=100 i kuponie PMT=12.0.

6.11.4. Zmodyfikowane duration \(M_D\)

Zmodyfikowane duration jest zdefiniowane jako:

\[M_D = \frac{D}{(1+r)}\]

Znaczy to, że między ceną obligacji a zmodyfikowaną duration zachodzi związek:

\[\Delta P = -P M_D \Delta r\]

Tak więc \(M_D\) mierzy czułość zmian % zmiany ceny obligacji względem zmiany jej rentowności.

Jest to niezłe narzędzie oceny ryzyka instrumentów dłużnych.

6.11.5. Wypukłość

O ile duration jest miarą pierwszego rzędu stopy procentowej bo mierzy nachylenie krzywej wartości bieżącej dla danej stopy YTM, to wypukłość jest miarą drugiego rzędu. Mierzy ona krzywiznę krzywej wartości bieżącej stopy procentowej. Duration służy do oceny ryzyka stopy procentowej. Lepszą ocenę ryzyka można jednak uzyskać dodając wyraz drugiego rzędu rozwinięcia funkcji ceny obligacji P w szereg Taylora. Wyraz drugiego rzędu w tym rozwinięciu związany jest z wypukłością (convexity) obligacji i odpowiada za stopień krzywizny relacji ceny od wartości YTM.

Pojęcie wypukłości jest zwykle przydatne przy omawianiu metod zarządzania portfelem obligacji.

Cena obligacji zależy od stopy procentowej, terminu zapadalności. Różniczkując dwukrotnie funkcje ceny obligacji względem \(r\) czyli:

\[P_o=\sum\limits_{i=1}^n\frac{C_i/m}{(1+r/m)^i} +\frac{P_N}{(1+r/m)^n}\]

Rozwijając funkcje w szereg Taylora i ograniczając się do drugiego wyrazu rozwinięcia można wykazać równość:

\[F(x + \Delta x) = \ f(x) +\Delta x\frac{\delta f}{\delta x} + 1/2! \frac{\delta^2 f(x)}{\delta x^2}(\Delta x)^2\]

Gdy za funkcje \(f(x)\) weżmiemy cenę obligacji, możemy rozwinięcie tej funkcji doprowadzić do postaci:

\[\Delta P_d =-M_D P_d (\Delta r) + (C/2)P_d (\Delta r)^2\]

gdzie \(C\) - jest wypukłością obligacji.

Można wykazać, że wypukłość wzrasta z kwadratem zapadalności. Maleje ze wzrostem wartości kuponu i rentowności.

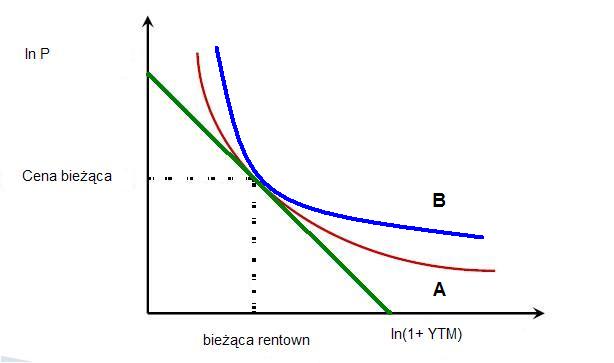
Rysunek obok pokazuje cechy tej miary ryzyka stopy procentowej na przykładzie dwu obligacji, obligacji A i obligacji B.

Obligacje te są na rynku w tej samej cenie i maja taką samą rentowność do zapadalności (YTM) i maja taka samą „duration”. Obligacja B jest bardziej wypukła niż obligacja A. Obligacja B jest bardziej pożądana przez inwestorów w porównaniu z A. Dlatego, że będzie zawsze generować lepsze wyniki inwestycji bez względu na to co stanie się ze stopami na rynku. Jeśli, przykładowo stopy wzrastają, cena B spadnie mniej niż cena A, a jeśli stopy spadają, cena B rośnie więcej niż wzrasta cena A.

Wysoka wypukłość to niezwykle pożądana cecha obligacji z punktu widzenia ryzyka.