7. Struktura terminowa stóp procentowych

7.1. Podstawowe zależności

Jeśli mamy do czynienie z instrumentem dłużnym generującym określoną stopę zwrotu w określonym czasie. Ponadto, jeśli inwestujemy kwotę inwestycji na końcu każdego etapu na okres następny, w którym stopa procentowa może być inna albo taka sama to mamy do czynienia z inwestycją wieloetapową.

Jeśli zdefiniujemy zwrot z inwestycji jako:

(1)\[R = \frac{S - S_0}{S_0},\]

gdzie: \(S\) końcowa wartość naszego portfela a \(S_0\) to jego wartość początkowa.

Jeśli w portfelu mamy instrument dłużny (instrument stałego dochodu) o stopie procentowej w danym okresie \(i\) równej \(r_i\), to licząc wartości portfela w kolejnych etapach inwestowania otrzymujemy:

\begin{alignat*}{4} S_1 = &\; S_0 (1+ r_1) \\ S_2 = &\; S_1 (1+ r_2) = S_0 (1+ r_1) (1+ r_2) \\ S_3 = &\; S_2 (1+ r_3) = S_0 (1+ r_1) (1+ r_2) (1+ r_3)\\ \dots\quad\ & \\ S_n = &\; S_{n-1} (1 + r_n) = S_0 (1 + r_1) (1+ r_2) (1+ r_3)\cdots (1+ r_n) \end{alignat*}

Korzystając ze wzoru definiującego (1) widać, że zwrot z takiej wieloetapowej inwestycji wynosi:

(2)\[R = \prod_{i=1}^n (1+ r_i) - 1\]

Stopa średnia roczna to wielkość stopy, która stosowana do każdego roku inwestycji da końcowy wynik równy \(R\). Czyli:

(3)\[(r_s+1)^n = \prod_{i=1}^n (1+ r_i)\]

Stąd wynika wzór:

(4)\[r_s = \sqrt[n]{\prod_{i=1}^n (1+ r_i)} - 1\]

Inaczej \(r_s\) nosi nazwę średniej geometrycznej stopy zwrotu

Przypominamy, że w finansach występuje wiele rodzajów „średnich”. Należy zawsze pamiętać jak się je liczy i wiedzieć, że nie są to raczej średnie arytmetyczne. Średnia arytmetyczna w przypadku wieloetapowej inwestycji w instrument stałego dochodu była by średnią arytmetyczną gdyby w każdym etapie inwestowana była ta sama wartość portfela. Dla takich samych \(r_i\) i takich samych \(i\) średnia geometryczna stopa zwrotu jest zawsze mniejsza lub równa średniej arytmetycznej stopie zwrotu.

7.2. Krzywa dochodowości

Związek miedzy dochodowościami obligacji a czasem ich życia określa krzywa zwana krzywą dochodowości. Konstrukcja krzywej dochodowości jest tylko łatwa jeśli dysponujemy jednorodnymi obligacjami o różnych datach zapadalności pozwalających na konstrukcje tejże krzywej. Ten zbiór danych powinien zawierać wszystkie kolejne daty zapadalności. Największy problem to właśnie założenie istnienia jednorodnego zbioru obligacji o różnej zapadalności. Obligacje raczej nie są jednorodne czyli mogą charakteryzować się nie tym samym ryzykiem i nie musi charakteryzować ich dużą i taka sama płynność. Z tych przykładowo powodów strukturę terminowa stóp procentowych określa się na podstawie krzywej dochodowości dla wybranych obligacji, przykładowo o tym samym oprocentowaniu, czy też biorąc pod uwagę stopę zwrotu do zapadalności.

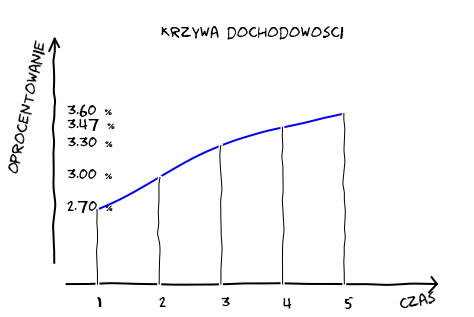
Krzywa dochodowości

Stopy spot to stopy oprocentowania pożyczek dzisiaj: rok, 2 lata, 5lat, 10 lat, etc… Krzywa rentowności to pokazanie aktualnych stóp spot dla różnych zapadalności. Z kształtu krzywej rentowności inwestorzy optymalizują swe działania inwestycyjne. Decydują czy lepiej reinwestować środki na okresy krótsze czy dłuższe. Stopy spot to stopy realnie występujące na rynku.

Stopy forward to stopy, których okres odsetkowy rozpocznie sie w przyszłości. Stopy forward sa implikowane przez instrumenty finansowe. Stopy forward można wyliczyć z wartości stóp spot. Wyliczanie stop forward ilustrować może poniższy przykład. Przykładowo, przyjmijmy hipotetycznie istniejące instrumenty dłużne, które obserwujemy na hipotetycznym rynku. Instrumenty te są instrumentami emitowanymi przez Skarb Państwa (hipotetycznego) więc możemy przyjąć, że są to instrumenty o minimalnym ryzyku na naszym rynku i o ryzyku podobnym. Przyjmijmy ponadto, że instrumenty te mają wartość nominalna jednakową - powiedzmy 100 000.

Tak więc bierzemy pod uwagę:

1. Jednoroczny bon skarbowy sprzedawany na rynku po 86 956.

2. Skarbową obligację dwuletnią wypłacającą kupon 15.5% i handlowaną po 100060

3. Trzyletnią obligację skarbową o kuponie 16.2% handlowaną po 100680.

Aby określić stopy forward postępuje się następująco. Z danych bonu skarbowego wyliczamy stopę roczną:

\[86956 = \frac{100 000}{1+r_1}\]

stąd \(r_1 = 15\%\).

Z danych obligacji dwuletniej wyliczamy stopę roczną za drugi rok - \(r_2\):

\[100060 = \frac{15500}{ 1 + r_1} + \frac{115500}{( 1+r_1)(1+r_2)}\]

stad \(r_2 =16\%\).

Z danych obligacji trzyletniej otrzymujemy:

\[100680 = \frac{16200}{1 + r_1} + \frac{16200}{ (1+r_1) (1+r_2)} + \frac{116200}{(1+r_1)(1+r_2)(1+r_3)}\]

Stad \(r_3 = 17\%\).

Sprawdźmy te obliczenia wykorzystując Sage:

Przy czym należy podkreślić, że \(r_2\) to stopa roczna dla roku drugiego życia obligacji, a \(r_3\) to roczna stopa oprocentowania „za dwa lata” na rok trzeci.

W przypadku stóp forward użytecznym jest następujące oznaczenie:

Stopy forward to oprocentowanie dla pożyczki zawartej w przyszłości - \(F\):

• \(F(1,1)\) oprocentowanie rocznej pożyczki zawartej w terminie 1 rok od dziś

• \(F(1,2)\) oprocentowanie 2 letniej pożyczki zawartej w terminie rok od dziś.

• \(F(2,1)\) oprocentowanie jedno rocznej pożyczki zawartej w terminie 2 lat od dziś

Stopa spot to szczególny przypadek - \(S(1) = F(0,1)\)

Zasadę tę ilustruje rysunek poniżej:

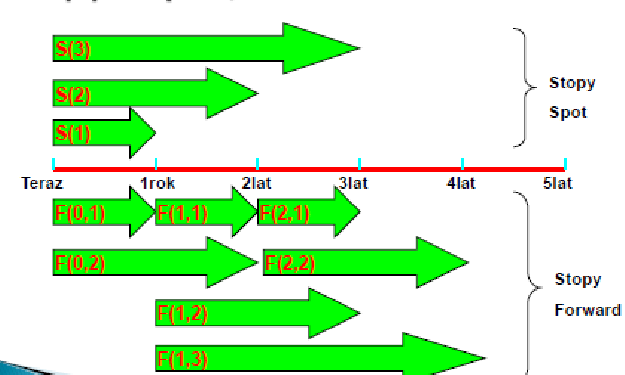
Zbiór stóp forward i związanych z nimi stóp „spot”.

Przyjmijmy, że na rynku znajdujemy dwuletni bon skarbowy A o rentowności rocznej 3.52% a bon roczny B, ma roczną rentowność równa 3.12%. Aby określić stopę forward \(F(1,1)\), widzimy że inwestując w bon A jednostkę pieniędzy otrzymujemy:

\[\text{Bon A: }\; ( 1 + 0.0352)( 1 + 0.0352)= 1.0716\]

Czyli ok. 7.2% zwrotu. Inwestując natomiast w bon B na rok jednostkę pieniędzy inwestujemy ja na 3.15% ale możemy otrzymany wynik reinwestować na kolejny rok na stopę \(F(1.1)\). Zakładając, że na rynku nie istnieje możliwość arbitrażu, to obie te strategie muszą dać ten sam efekt inwestycji. Czyli:

\[(1+ 0.0312) ( 1+ F(1.1)) = ( 1 +0.0352)( 1 + 0.0352)\]

Stąd:

\[( 1 + F(1.1,) )= ( 1 + 0.0352)( 1 + 0.0352)/1.0312 = 1.0392\]

Czyli \(F(1.1)\) musi wynosić 3.92 % rocznie.

Można postąpić również odwrotnie. Znając zestaw stóp forward możemy wyliczyć stopy spot. Załóżmy, że stopa \(F(0.1)\) wynosi 2.5% a \(F(1.1)\)) wynosi 3.2%. Należy wyliczyć \(S(2)\). Postępujemy tak jak poprzednio i porównujemy do siebie dwie możliwe strategie inwestycyjne. Inwestujemy jednostkę pieniężną albo:

1. Na dwa lata przy stopie \(S(2)\), co daje:

   \[(1+ S(2))( 1+ S(2))= (1+ S(2))^2\]

2. Inwestujemy jednostkę pieniężną na pierwszy rok przy stopie \(F(0.1)\) a następnie efekt inwestycji reinwestujemy na kolejny rok przy stopie \(F(1.1)\) czyli:

   \[(1+ 0.02)(1+ 0.032)=1.05264\]

   około 5.27% a to powinno być równe inwestycji 1.

Innymi słowy:

\[(1+ S(2))^22 = (1+ 0.02)(1+ 0.032).\]

Stąd

\[(1+S(2)) = \frac{1}{2}[(1+ 0.02)(1+0.032)]= 1.027\]

czyli \(S(2) = 2.7\%\).

W ostatnim przykładzie wyliczona stopa spot jest średnią geometryczną stóp zwrotu forward. Czego należało się spodziewać, mając na uwadze wzór (4).

Wiedząc, że:

\[\sqrt[n]{a_1 a_2\dots a_n} \le \frac{1}{n}\sum_{i=1}^n a_i\]

Możemy używać średniej matematycznej do szacowania średniej geometrycznej.

7.3. Modele dyskretne ewolucji stóp procentowych

Stopa forward to stopa terminowa czyli „pojawiająca” się za pewien czas. Można interpretować ją jako ewolucje stopy spot. Gdyby nie istniała niepewność na rynku co do scenariusza dalszego jego rozwoju to stopa foward byłaby nielosowa i z góry znana. Jednakże istniejąca niepewność przyszłości zmusza nas do ustawicznego modelowania ewolucji stopy forward jako procesu stochastycznego.

Stopy forward pokazują ewolucje stóp na rynku. Więc należy tą ewolucje śledzić mając na uwadze efektywne zarządzanie portfelem instrumentów dłużnych. Temu celowi służy tworzenie modelu aby wyjaśnić ruch stóp forward. Następnie wyliczamy krzywą rentowności wynikającą ze stóp forward i porównujemy ją z krzywą stóp aktualnych. Modelowanie polega przykładowo na stworzeniu modelu dwumiennego (stopa zmieniać się może okresowo poprzez wzrost lub zmalenie) albo modelu trójmiennego, gdy wartośc stopy w kolejnym okresie czasu z określonym prawdopodobieństwem zmienia się w górę lub w dół albo nie zmienia się w ogóle.

Rozważając modele dwumienne, należy odróżnić dwa zasadnicze typy - drzewa rekombinujące i nierekombinujące. Te pierwsze mają w każdym kolejnym okresie dokładnie o jedną unikalną wartość stopy procentowej więcej. Te drugie mają po każdym okresie dwa razy więcej wartości stopy procentowej, co implikuje wzrost liczby stanów z liczbą okresów jak \(2^n\).

Rozważmy przykład drzewa binarnego rekombinującego. Niech w chwili \(t=0\) stopa procentowa wynosi \(4\%\). Czyli \(F(0,1) = S(1)\). Stopa może ewoluować w czasie i przyjmujęmy regułę, że z prawdopodobieństwem \(50\%\) może wzrosnąć o \(0.7\%\) do wartości \(4.7\%\) albo spaść o \(0.2\%\) do wartość \(3.8\%\) z tym samym prawdopodobieństwem \(50\%\). Graficznie przedstawiamy to w następujący sposób:

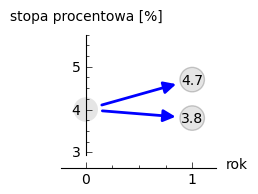
Mamy więc dwa scenariusze, nazywane tutaj ścieżkami:

Ścieżka 1,

w której stopa wzrasta ze skumulowanym zwrotem \(1.04\times1.047 = 1.089\)

Ścieżka 2,

w której stopa maleje ze skumulowanym zwrotem \(1.04\times1.038 = 1.08\).

Skumulowany średni zwrot z dwu lat będzie średnią arytmetyczną z dwóch powyższych scenariuszy i wynosi:

\[\frac{1}{2} \text{Ścieżka 1} + \frac{1}{2} \text{Ścieżka 2} = \frac{1}{2} 1.09 + \frac{1}{2} 1.079 = 1.085\]

czyli \(8.5\%.\) Zanualizowany zwrot czyli \(S(2)\) jest równy:

\[1.085\frac{1}{2} = 1.042\]

czyli \(4.2\%\).

W kolejnym okresie mamy trzy stany i cztery różne scenariusze dojścia do nich:

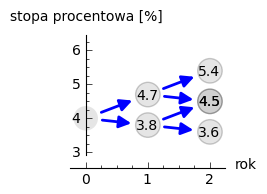
Policzmy rentowności.

• Ścieżka 1

  \(1.04\times1.047\times1.054 = 1.148 \text{ czyli } 14.8 \%\)

• Ścieżka 2

  \(1.04\times1.047\times1.045 = 1.138 \text{ czyli }13.8 \%\)

• Ścieżka 3

  \(1.04\times1.038\times1.045 = 1.128 \text{ czyli }12.8 \%\)

• Ścieżka 4

  \(1.04\times1.038\times1.036 = 1.118 \text{ czyli } 11.8 \%\)

Skumulowany zwrot po trzech okresach (np. latach) wynosi:

\[\frac{1}{2} \langle 1.148 + 1.138 + 1.128 + 0.25 x 1.118 \rangle = 1.133\]

Zanualizowany zwrot po trzech okresach \(S(3)\) wynosi:

\[\sqrt[3]{ 1.128} - 1 = S(3) \text{ czyli około } 4.25\%\]

W podobny sposób dla dowolnych ścieżek możemy obliczać odpowiednie stopy. Jednak ze względu na wykładniczy wzrost liczby ścieżek z liczbą okresów warto zastosować komputer do obliczenia średniej po ścieżkach. Spróbujmy więc zaimplementować powyższy algorytm korzystając z systemu Sage.

Po pierwsze zdefiniujmy sobie procedurę, która będzie generowała rekombinujące drzewo binarne. Nazwijmy tą funkcję gen_recombining(), jej szczegółowy opis znajduję się w Dodatek: Komputerowa analiza drzew binarnych.

Drzewo w którym wszystkie wartości rekombinują posiada \(n+1\) wartosci w \(n\) - tym okresie. Mamy dwie proste reguły prowadzące do tego typu drzew. Jedną jest odejmowanie i dodawania tych samych wartości, co ma to jednak tę wadę, że możemy wygenerować ujemną stopę procentową. Drugą możliwością jest mnożenie wartości stopy procentowej w przypadku wzrostu przez pewną liczbę większą od jednego, a w przypadku zmalenia przez jej odwrotność. Łatwo się przekonać, że takie działanie zawsze prowadzi do drzewa rekombinującego.

Poeksperymentuj sam

Wykonaj poniższy kod!

Do wizualizacji danych możemy wykorzystać również system Sage i przykładowa procedura rysującą drzewa w obu formatach ma następującą postać:

Teraz możemy narysować drzewo do np. czwartej generacji i tak wywołanie:

print( gen_recombining(SP=4,3) )

powinno dać:

\[\left[4.0\right] \left[4.7, 3.4\right] \left[5.5, 4.0, 2.9\right] \left[6.5, 4.7, 3.4, 2.5\right]\]

Poeksperymentuj sam

Wykonaj poniższy kod dla różnych parametrów, niter,SP,q=0.175,delta1,delta2!

Obliczanie wartości średnich w modelu dwumiennym wiąże się z sumowaniem po wszystkich ścieżkach. Ponieważ rozważania dla stóp procentowych mają sens dla kilku - maksymalnie kilkunastu lat to można sobie pozwolić na dokładne wykonanie takich obliczeń. Liczba składników sum będzie np. \(65536\) dla \(n=16\).

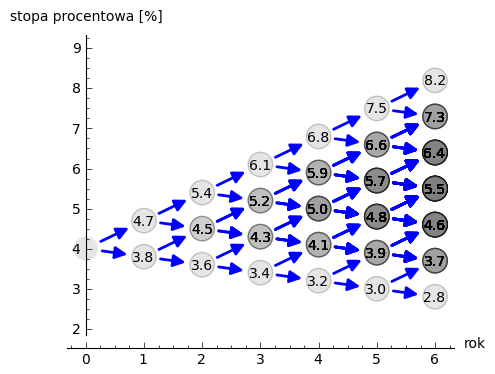
Mając drzewo binarne, możemy policzyć średnią zanulizowaną stopę procentową. Algorytm, można zapisać w trzech liniach:

SP = gen_recombining(N,delta1=0.7,delta2=0.2)
all_paths = map(lambda x:[0]+np.cumsum(x).tolist(), map(list,cartesian_product(N*[[0,1]]).list() ))
mean( [prod([(1+0.01*SP[i][p]) for i,p in enumerate(path_)]) for path_ in all_paths] )

Opis programu

Chcemy policzyć średnią z iloczynów \(\prod_{i=1}^{n} (1+r_i)\) po wszystkich ścieżkach. Postępujęmy w następujący sposób:

• linia 1: - generujemy drzewo (rekombinujące) wszystkich wartości stóp: SP = gen_recombining(N,...

• linia 2: - wyliczamy wszystkie ścieżki w formacie np. [0,1,2,1,…], gdzie kolejne liczby oznaczają pozycję danej stopy w odpowiednim okresie. W przykładzie, w trzecim okresie mamy stopę numer „2” na liście stóp. Obliczenia te wykorzystują iloczyn kartezjanski, który w Sage mamy w postaci funkcji np. dla dwóch list: cartesian_product([[0,1],[0,1]])

  • zauważmy, że pierwsza gwiazdka „rozpakowywuje argumenty” z N*[[0,1]].

  • użycie np.cumsum umożliwia z zapisu względnych ruchów stopy w okresach [0,1,0,0,1] do jej bezwględnych indeksów wartości [0, 1, 1, 1, 2].

• linia 3: - mając już zapis każdej ścieżki w powyższym formacie, wykonujemy odpowiedni iloczyn oraz uśredniamy wynik po ścieżkach

Możemy sprawdzić czy powyższy program obliczy poprawnie testując go na przeliczonym w uprzednio przykładzie:

Wykonując powyższą komórkę powinniśmy otrzymać wynik taki sam jak w rachunkach „na piechotę”. Po co nam więc algoryym? Rachunków „na piechotę” nie da się przeprowadzać dla zbyt dużej ilości okresów, bo liczba scieżek rośnie wykładniczo jak \(2^N\)! A w następnym rozdziale będziemy potrzebowali wyników dla \(N>10\).

7.3.1. Krzywa dochodowości w modelu dyskretnym

Mając napisany algorytm do oblicznania średniej zanualizowanej stopy, możemy policzyć krzywą dochodowości w modelu dwumiennym. W tym celu liczymy, zakładając ewolucję stopy zgodnie z regułami- multyplikatywną lub addytywną, stopę \(r_s\) dla różnych ilości okresów i nanosimy otrzymane wartości na wykresie \(r_s(N)\). Mamy:

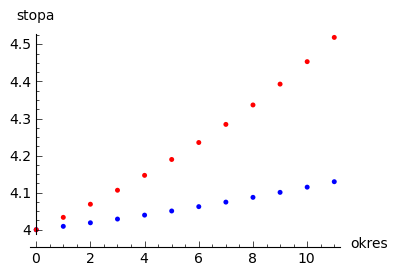
Krzywa rentowności dla ewolucji stopy procentowej modelowanej procesem binarnym

Implementacja algorytmu w zasadzie polega na umieszczeniu kodu liczącego zanulizowaną średnią stopę po \(N\) okresach wewnątrz funkcji, w której parametrem będzie właśnie liczba okresów.

Poeksperymentuj sam

W funkcji forward_rate(N = 2,**kpars) oznaczenie **kpars umożliwia przekazanie dowolnej ilości argumentów, które będą potem przekazane dalej do gen_recombining(N,**kpars). Można na przykład zastosować wywołanie z drzewem addytywnym. Jak wtedy będzie wyglądała ta krzywa?

7.4. Modele ciągłe ewolucji stóp procentowych

Ewolucję stopy procentowej można też modelować procesem losowym z czasem ciągłym. Modele takie dzielą się na:

• jednofaktorowe: takie w których mamy jedno równanie stochastyczne

• wielofaktorowe: mamy dwa lub więcej równań stochastycznych

Wszystkie te modele są zbudowane na podstawie teorii o bardzo podobnych założeniach jak model Blacka-Scholesa. Rozważmy, bezkuponową obligację skarbową istniejący na rynku z ciągła kapitalizacją odsetek. Yield to Maturity takiej obligacji spełnia równanie:

gdzie \(P(t,t+T)\) to cena tej obligacji w chwili \(t\) a \(T\) to okres czasu po jakim on zapada. Rozwiązując to równanie na YTM dostajemy:

(5)\[Y(t,T) = -\frac{1}{T}\log(P(t,t+T)).\]

Z drugiej strony średnia po czasie z ciągłej stopy forward daje wewnętrzną stopę zwrotu w okresie do zapadalności:

(6)\[Y(t,T) = \frac{1}{T}\int_t^{t+T} F(t,s)ds.\]

Z powyższych dwóch równań otrzymujemy związek między ciągłą stopą forward a ceną rozważanej obilgacji:

(7)\[F(t,s) = -\frac{\partial}{\partial s} \log P(t,s).\]

Załóżmy, że chwilowa stopa procentowa jest procesem losowym spełniającym następujące równanie stochastyczne

(8)\[dr = \mu(r,t) dt + \sigma(r,t) dW\]

Ponieważ cena obligacji jest funkcją tego procesu, zastosujemy wzór Ito (patrz skrypt Dynamika Stochastyczna:

\[dP = \left( \frac{\partial P}{\partial t} + \mu(r,t) \frac{\partial P}{\partial r} +\frac{\sigma(r,t)^2}{2} \frac{\partial^2 P}{\partial r^2} \right) dt + \sigma(r,t)\frac{\partial P}{\partial r} dW\]

Dzieląc przez \(dt\) i uśredniając po realizacjach procesu losowego otrzymujemy:

(9)\[\langle \frac{dP}{dt}\rangle = \frac{\partial P}{\partial t} + \mu(r,t) \frac{\partial P}{\partial r} +\frac{\sigma(r,t)^2}{2} \frac{\partial^2 P}{\partial r^2}\]

Teraz należy poczynić założenia co do ewolucji wielkości oczekiwanej: \(\langle \frac{dP}{dt}\rangle\). Można by przypuszczać, że średnia cena takiej obligacji powinna rosnąć zgodnie z równaniem:

\[\langle \frac{dP}{dt}\rangle = r P,\]

Jednak przyjmuje się, że w sytuacji gdy mamy ryzyko wzrost ten powinien być większy by skompensować ewentualne straty. Dlatego wprowadza się dodatkowy parametr, który jest zwany risk premium i równanie to przybiera postać:

(10)\[ \langle \frac{dP}{dt}\rangle = r (1-\lambda) P.\]

Podstawiając do równanie (10) do (9) otrzymujemy cząstkowe równanie różniczkowe na cenę obligacji bezkuponowej z losową stopą procentową daną przez (8).

(11)\[\frac{\partial P}{\partial t} + \mu(r,t) \frac{\partial P}{\partial r} +\frac{\sigma(r,t)^2}{2} \frac{\partial^2 P}{\partial r^2} - r (1-\lambda) P\]

Powyższe rozważania są dość ogólne, zauważmy, że nie podaliśmy jawnych postaci funkcji \(\sigma(r,t)\) i \(\mu(r,t)\). Jednym z podstawowych modeli jednofaktorowych jest tzw. model Vasicek’a, w którym chwilowa stopa zwrotu dana jest równaniem:

(12)\[\frac{dr}{dt} = \alpha \left( \gamma - r(t) \right) + \sigma \xi(t),\]

gdzie:

• \(r(t)\) - chwilowa stopa zwrotu

• \(\lambda\) - prędkość relaksacji

• \(\gamma\) - wartość asymptotyczna procesu

• \(\xi(t)\) - biały szum Gaussowski z funkcją korelacji: \(\langle x(t) x(t+\tau) \rangle = \delta(\tau)\)

Informacja

Proces ten jest też zwany procesem Ornsteina-Uhlenbecka i w fizyce może być interpretowany jako dynamika przetłumionego oscylatora harmonicznego z szumem.

Jesli zastosujemy model Vasicka (12) to równanie (11) upraszcza się do:

(13)\[\frac{\partial P}{\partial t} + \alpha \left( \gamma - r \right) \frac{\partial P}{\partial r} +\frac{\sigma^2}{2} \frac{\partial^2 P}{\partial r^2} - r (1-\lambda)P\]

Okazuje się, że to równanie można rozwązać dokładnie i rozwiązanie bez czynnika risk premium jest w postaci:

\[P(r,0,T) = Ae^{-Br},\]

gdzie:

\[\begin{split}B = \frac{1}{\alpha} (1-e^{-\alpha T}) \\ A = \exp\left\{ (\gamma-\frac{\sigma^2}{2 \alpha^2}) (B-T) - \frac{\sigma^2}{4\alpha} B^2 \right\}\end{split}\]

Uwzględnienie czynnika \(\lambda\) sprowadza się do zastąpienia pamametrów \(\alpha,\gamma\):

\[\begin{split}\alpha \to \alpha + \lambda\sigma \\ \gamma \to \alpha \frac{\gamma}{\alpha+\lambda \sigma}\end{split}\]

Poeksperymentuj sam

Wykonaj poniższy kod implementujący wzór na cenę zerokuponowej obligacji. Narysuj krzywą dochodowości, czyli Yield to Maturity dla tej obligacji. Poeksperymentuj z poniższą komórką i parametrami.

Możemy sobie łatwo skonstruować algorytm, który będzie symulował to równanie stochastyczne (12). Ponieważ potrzebujemy wiele realizacji procesu losowego, najlepiej będzie symulować jednocześnie \(M\) trajektorii.

Opis programu

Wykorzystujemy stochastyczny algorytm Eulera w którym całka z białego szumu jest równa:

\[\int_0^h \xi(t) dt = \sqrt{h} N(0,1),\]

gdzie \(N(0,1)\) jest zmienną losową o rozkładzie Gaussowskim ze średnią zero i wariancją \(1\).

• inicjalizujemy macierz x w której będziemy przechowywać wszystkie \(N\) kroków dla \(M\) trajektorii

• w pierwszej kolumnie tej macierzy umieszczamy wartości początkowe dla wszystkich realizacji - x[:,0] = r0*np.ones(M)

Mając już wygenerowane trajektorie możemy je narysować:

Pozostaje tylko obliczenie krzywej dochodowości z symulacji stochastycznej i porównanie jej z wynikiem analitycznym:

Opis programu

• wykonujemy równoczesną symulację \(N\) trajektorii

• w linii P = np.average(np.exp(-np.cumsum(x,axis=1)*h),axis=0) obliczamy cenę obligacji dla każdej z realizacji procesu stopy i uśredniamy

• linia pDR = -np.log(P)[1:]/time[1:] oblicza YTM dla obligacji z jej ceny.

7.5. Podsumowanie

Struktura terminowa rynku stóp procentowych jest jednoznacznie opisana przez każdą z poniższych wielkości:

• cenę obligacji zerokuponowych \(P(t,s)\)

• Yield to Maturity tych obligacji \(Y(t,s)\)

• stopy forward \(F(t,s)\)

Formuły P_YTM (5) (7) (6), oraz ich dyskretne odpowiedniki umożliwiają przeliczenie jednej wielkości w drugą.

W modelowaniu struktury stop procentowych zazwyczaj zakłada się pewien model ewolucji stochastycznej chwilowej stopy procentowe. Z tego modelu metodami analitycznymi lub poprzez symulacje wycenia się obligaję zerokuponową. Mając wyznaczoną tą wielkość (\(P(t,s)\)) struktura terminowa rynku stop procentowych jednoznacznie określona.

Stopy forwards są potrzebne do obliczania parametrów FRA