Dynamika populacyjna: ciągłe modele jednowymiarowe¶
Model Malthusa¶
W przyrodzie występuje wiele gatunków zwierząt i roślin. Ich liczebność ciągle się zmienia: procesy są dynamiczne, powiązane między sobą, oddziaływania są skomplikowane, często losowe. Można powiedzieć, że jest to niewątpliwie przykład realnego układu złożonego z wielu elementów połączonych z sobą w skomplikowaną sieć. Opis takich układów jest trudny. Jak to często bywa w naukach przyrodniczych, stosuje się opis przybliżony, „gruboziarnisty”, pomija się elementy mniej istotne i uwzględnia się najważniejsze składniki układu. Jest to metoda idealizacji nagminnie stosowana przez fizyków do opisu rzeczywistości. Historia pokazuje, że metoda ta nie jest zła. Ba, czasami bardzo dobra i nawet znakomita.
Podobne podejście zastosujemy do opisu dynamiki populacyjnej. Zaczniemy od najprostszego modelu: jedna populacja. Może to być populacja ludzi na określonym obszarze, populacja zajęcy, bakterii czy populacja komórek nowotworowych. Może to być „populacja” związku chemicznego (molekuł). Populację określa się liczbami naturalnymi: jest 4 tys. ludzi, 3 mld bakterii, 10 20 molekuł. Posługiwanie się liczbami całkowitymi jest trudne w modelowaniu. Postąpimy podobnie jak w opisie dynamiki płynów, np. wody czy krwii. Woda w szklance składa się z dyskretnej liczby molekuł. Ale nikt do charakterystyki wody nie stosuje opisu bazyjącego na liczbach naturalnych. Stosujemy przybliżenie ośrodka ciągłego scharakteryzowanego gęstością wody: ilością molekuł w jednostkowej objętości. Podobny opis zastosujemy w modelowaniu dynamiki populacyjnej. Liczba N charakteryzująca liczbę osobników w populacji będzie nieujemną liczbą rzeczywistą, interpretowaną jako względna liczba osobników (liczba osobników w stosunku do np. średniej liczby osobników w ostatnich 50 latach lub maksymalnej liczby osobników w poprzednim roku, itp.). Liczba ta może zmieniać się w sposób ciągły. Liczba N(t) będzie charakteryzować liczbę osobników populacji w chwili czasu t. Zmiana w czasie tej funkcji wynika z zastosowanego modelu.
Modele będziemy budować bazując na wiedzy z teorii funkcji i obserwacjach otaczającego nas świata. Nie trzeba być wybitnym matematykiem, żeby umieć zinterpretować różnicę dwóch prędkości samochodu A i samochodu B gdy samochód A jedzie z prędkością 40 km/h, a samochód B jedzie z prędkością 150 km/h. Wielkość, która mówi o tempie zmiany położenia w czasie to pochodna położenia jako funkcji czasu, czyli prędkość. To właśnie pochodna mówi nam, w jakim tempie zmienia się dana wielkość. Jeżeli pochodna jest dodatnia, to funkcja rośnie; gdy pochodna jest ujemna, to funkcja maleje. Oto niezbędna wiedza, aby zacząć modelowanie.
Pierwszy krok modelowania: dlaczego zmienia się liczba osobników N(t) w danej populacji? Można wyróżnić trzy podstawowe procesy: ktoś się rodzi, ktoś umiera, jeszcze inny „wyjeżdża”, emigruje, opuszcza populację, a jeszcze inny „przyjeżdża”, imigruje. W języku matematyki możemy to zapisać w postaci relacji:
Lewa strona tej relacji opisuje tempo zmiany populacji: \(dN(t)/dt\)
przyrost populacji wskutek urodzin nowych osobników jest rosnącą funkcją \(f(N)\) liczby osobników \(N\) w populacji: W populacji 1 mln rodzi się więcej osobników niż w populacji 50 tys. (jak można zaobserwować w ostatnich latach, w populacji ludzi nie musi to być prawdą). Najprostszą funkcją jest funkcja liniowa:
gdzie współczynnik \(a \gt 0\) nazywa się tempem rozmnażania (wzrostu) populacji.
ubytek populacji wskutek śmierci osobników jest rosnącą funkcją \(g(N)\) liczby osobników w populacji: W populacji 1 mln umiera więcej osobników niż w populacji 50 tys. Najprostszą funkcją jest funkcja liniowa:
gdzie współczynnik \(b \gt 0\) jest tempem śmiertelności (zaniku) populacji .
Pominiemy na obecnym etapie procesy migracji (zaczynamy od najprostszego modelu!). Z powyższych rozważań wynika taki oto model:
Otrzymaliśmy liniowe równanie różniczkowe zwyczajne pierwszego rzędu. Aby otrzymać jego jednoznaczne rozwiązanie, musimy jeszcze zadać warunek początkowy:
Jest to proste równanie różniczkowe, które można rozwiązać metodą rozdzielenia zmiennych:
Z rozwiązania tego wynika, że:
jeżeli tempo rozmnażania jest takie samo jak tempo śmiertelności, \(k=0\) czyli \(a=b\), to populacja utrzymuje sie na tym samym poziomie liczebności: \(N(t) = N(0)\).
jeżeli tempo rozmnażania jest większe niż tempo śmiertelności, \(k\gt 0\) czyli \(a \gt b\), to populacja rozrasta się: \(N(t) \gt N(0)\).
jeżeli tempo rozmnażania jest mniejsze niż tempo śmiertelności, \(k\lt 0\) czyli \(a \lt b\), to liczba osobników w populacji maleje: \(N(t) \lt N(0)\).
Powyższy model został zaproponowany przez Malthusa w 1798 roku. Wynika z niego eksponencjalnie szybkie tempo wzrostu (gdy a>b) lub eksponencjalnie szybki zanik populacji (gdy a<b). Są takie przykłady, dla których model Malthusa realizuje się w pewnych przedziałach czasu, w szczególności w początkowych fazach wzrostu (np. wzrost kolonii bakterii w odpowiednich warunkach).
Wykorzystanie Sage do analizy modelu Malthusa¶
Rozwiązanie analityczne
W SAGE można bardzo łatwo otrzymać postać analityczną rozwiązania równania Malthusa, patrz poniżej:
sage: var('t k')
sage: #k=1
sage: assume(t>0)
sage: N = function('N',t)
sage: row = N.diff()== k*N
sage: rozw = desolve(row,N,ivar = t)
sage: rozw
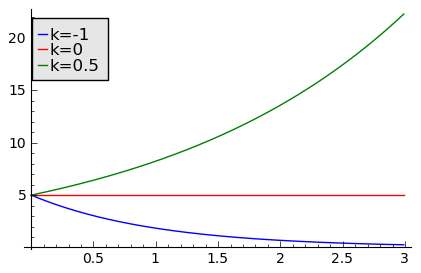
Wykres pokazujący wzrost, brak zmian i zanik populacji w zależności od wartości parametru k=a-b
sage: var('N1,N2,N3')
sage: T = srange(0,3,0.01)
sage: sol=desolve_odeint( vector([-N1, 0, 0.5*N3]), [5,5,5],T,[N1,N2,N3])## rozwiązania dla różnych wartości k=-1, 0, 0.5
sage: line( zip ( T,sol[:,0]) ,figsize=(5, 3),legend_label="k=-1") +\
... line( zip ( T,sol[:,1]) ,color='red',legend_label="k=0")+\
... line( zip ( T,sol[:,2]) ,color='green',legend_label="k=0.5") ## pokazujemy rozwiązania dla różnych wartości k=-1, 0, 0.5
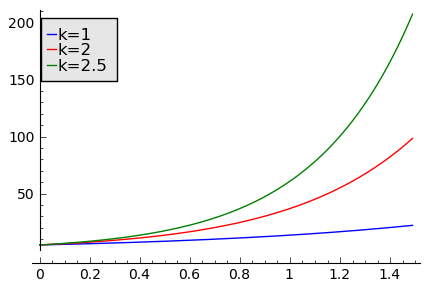
Wykres pokazujący różne tempo wzrostu w zależności od wartości parametru k=a−b > 0
sage: T1 = srange(0,1.5,0.01)
sage: sol1=desolve_odeint( vector([N1, 2*N2, 2.5*N3]), [5,5,5],T1,[N1,N2,N3])
sage: line( zip ( T1,sol1[:,0]) ,figsize=(5, 3),legend_label="k=1") +\
... line( zip ( T1,sol1[:,1]) ,color='red',legend_label="k=2")+\
... line( zip ( T1,sol1[:,2]) ,color='green',legend_label="k=2.5") ## pokazujemy rozwiązania dla dodatnich wartości k=1, 2, 2.5
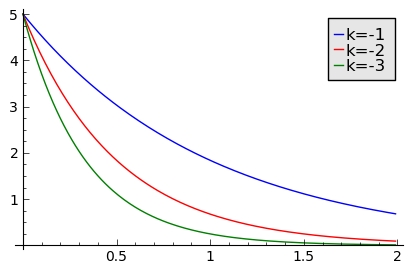
Wykres pokazujący różne tempo zaniku populacji w zależności od wartości parametru k=a−b < 0
sage: T2 = srange(0,2,0.01)
sage: sol2=desolve_odeint( vector([-N1, -2*N2, -3*N3]), [5,5,5],T2,[N1,N2,N3])
sage: line( zip ( T2,sol2[:,0]) ,figsize=(5,3),legend_label="k=-1") +\
... line( zip ( T2,sol2[:,1]) ,color='red',legend_label="k=-2")+\
... line( zip ( T2,sol2[:,2]) ,color='green',legend_label="k=-3") ## pokazujemy rozwiązania dla ujemnych wartości k=-1, -2, -3
ZADANIE: Dane eksperymentalne dotyczące wzrostu bakterii Vibrio natrigens są nastepujace (patrz http://mathinsight.org/bacteria_growth_initial_model)
t (min)
N (gęstość)
0
0.022
16
0.036
32
0.060
48
0.101
64
0.169
Vibrio natrigens
Sprawdź, czy model Malthusa opisuje powyższy wzrost kolonii bakterii. Oceń rzetelność tego modelu.
sage: t = [0 , 16 , 32 , 48 , 64 ]
sage: X = [0.022, 0.036, 0.060, 0.101, 0.169 ]
W modelu Malthusa, wzrost jest eksponencjalny. Więc w skali logarytmicznej otrzymujemy prostą:
\(y(t) = \ln N(t) = \ln N_0 + k t = c + k t\)
Przedstawiamy dane wzrostu bakterii na skali logarytmicznej:
sage: point(zip(t,map(log,X)),color='red',figsize=4)
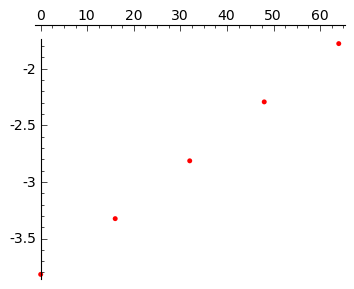
Z grubsza wygląda to na linię prostą. Aby to sprawdzić, wykonamy procedurę dopasowania danych eksperymentalnych do krzywej: \(n(t) = c \; e^{ k t}\):
sage: var('x a b')
sage: model(x) = c * exp(k * x )
sage: fit = find_fit (zip(t,X), model, solution_dict=True,initial_guess=(.1,.1))
sage: fit
Parametr initial_guess ustala punkt startowy dla rozpoczęcia iteracji procedury nieliniowej optymalizacji.
sage: fit2 = find_fit (zip(t[:2],X[:2]), model, solution_dict=True)
sage: print fit2
sage: plot( model(x).subs(fit), (x,-20,70)) + plot( model(x).subs(fit2), (x,-20,70),color='green') + point(zip(t,X),color='red',figsize=4)
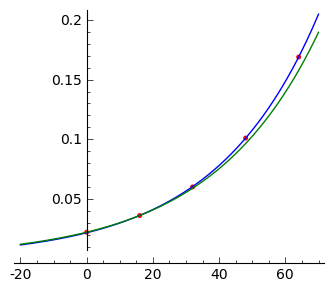
sage: log(0.036/0.022)/16
Ostatnia liczba to wartość \(k\) obliczona z danych dla wzrostu bakterii. Jest on bardzo bliska wartości b obliczonej z dopasowania danych do krzywej eksponencjalnej: \(n(t) = c \exp(k t)\). Stała \(c\) też jest bliska wartości \(0.022\) z danych.
ZADANIE: W modelu Malthusa występują 2 parametry: a i b. W rozwiązaniu pojawia się tylko różnica a-b. Przeprowadzić dyskusję dotyczącą bezwymiarowej postaci równania Malthusa. Ile istotnych parametrów zawiera model Malthusa?
ZADANIE: W roku 1960 liczba ludności wynosiła 3 mld. W roku 1970 - 3.7 mld ludzi. Zakładając, że zmiana populacji następuje zgodnie z powyższym modelem Malthusa, oblicz liczbę ludności w roku 1980. Porównaj wynik modelu ze stanem faktycznym (skorzystaj z danych demograficznych zamieszczonych na stronie internetowej).
Model Verhulsta¶
Załóżmy, że w modelu Malthusa uwzględniamy tylko procesy urodzin i pomijamy procesy śmierci, tzn. b=0. Wówczas populacja wzrasta w tempie wykładniczym:
co ilustruje powyższy rysunek dla przypadku k>0. Tak szybkie tempo wzrostu może być obserwowane dla pewnych układów tylko w niewielkim przedziale czasu. W ogólności zbyt szybkie tempo wzrostu populacji spowodowałoby zachwianie równowagi w przyrodzie. Na przykład w roku 1859 farmer Thomas Austin wypuścił w swoich włościach w Australii 24 króliki europejskie, licząc na to, że będzie mógł oddawać się przyjemnościom polowania. Inni farmerzy podchwycili pomysł i rzeczywiście - polować mogli wkrótce do woli. W roku 1869 królików w Australii było już tyle, że odstrzeliwano ich dwa miliony rocznie, bez żadnych widocznych ubytków w liczebności populacji. Króliki zdewastowały przyrodę Australii. Pożerały roślinność, przez co wymarło wiele gatunków australijskich ssaków. Udało się je wytępić dopiero w latach pięćdziesiątych ostatniego stulecia, sprowadzając na wyspę chorobę: myksomatozę. Wirus w ciągu dwóch lat zabił pół miliarda z sześciuset milionów królików. Pozostałe króliki były na chorobę odporne i ich liczebność znowu zaczęła wzrastać, dlatego w latach dziewięćdziesiątych ludzie pognębili je kolejną plagą, zwaną chińskim pomorem królików.
Z reguły nadmierny rozrost populacji na ograniczonym terenie powoduje trudny dostęp do pożywienia i tempo wzrostu populacji zaczyna spowalniać. Model uwzględniający ten efekt ograniczonego dostępu do pożywienia został po raz pierwszy zaproponowany przez Verhulsta w roku 1838. W modelu tym tempo wzrostu \(a\) nie jest stałe, ale zależy od stanu populacji:
i równanie ewolucji przyjmuje postać:
Zależność funkcyjna \(a(N)\) od \(N\) powinna mieć następującą własność: jeżeli populacja wzrasta, tempo wzrostu powinno maleć. Oczywiście jest wiele funkcji o tej własności: to są funkcje malejące. Verhulst zaproponował taką oto zależność:
gdzie \(r \gt 0\) jest parametrem o podobnej interpretacji jak parametr \(a\) w modelu Malthusa (charakteryzuje tempo wzrostu) oraz stała \(K \gt 0\) charakteryzuje zasoby pożywienia i czasami nazywa się pojemnością środowiska. Zauważmy, że stała \(K\) pojawia się w ilorazie \(N/K\) i jest charakterystyczną liczbą osobników \(K=N_c\) w populacji. Jeżeli \(N \gt K\) to \(a(N) \lt 0\) i populacja maleje. Z kolei jeżeli \(N \lt K\) to \(a(N) \gt 0\) i populacja rozrasta się.
Jak zmiana K wpływa na tempo wzrostu populacji? Jeżeli K rośnie to N/K maleje. Z kolei to powoduje, że 1-N/K rośnie, czyli a(N) rośnie. Oznacza to, że tempo wzrostu rośnie i populacja rozrasta się szybciej. Stąd wniosek: Wzrost parametru K powoduje szybsze tempo wzrostu populacji.
Z powyższych rozważań otrzymujemy równanie ewolucji w postaci równania Verhulsta:
Równanie to zawiera 2 parametry: r oraz K. Natomiast istotne, jakościowe a nie ilościowe własności układu nie zależą od tych parametrów. Aby pokazać od ilu parametrów zależą własności układu, należy przekształcić równanie Verhulsta do postaci bezwymiarowej. W tym celu zdefiniujemy względną liczbę osobników w populacji
oraz bezwymiarowy czas
W nowych zmiennych równanie Verhulsta przyjmuje postać:
Jak widać, w równaniu tym nie pojawiają się żadne parametry. Jest to istotne, gdyż własności układu nie zależą jakościowo od jakichkolwiek wartości r oraz K.
Zadanie
Znaleźć stany stacjonarne układu i zbadać ich stabilność.
\(f(x) =0\), tzn. \(x(1-x)=0\),
stąd otrzymujemy 2 stany stacjonarne \(x_1=0\) oraz \(x_2=1\)
ich stabilność: \(\lambda = f'(x) = 1- 2 x\),
czyli \(\lambda_1= f'(x_1) = 1 \gt 0\) (niestabilny), \(\lambda_2= f'(x_2) =-1 \lt 0\) (stabilny)
Ponieważ otrzymujemy jeden stabilny stan stacjonarny \(x=1\), wszystkie rozwiązania \(x(s)\) z warunkiem początkowym \(x_0 \gt 0\) dążą do tego stanu.
Gdy warunek początkowy \(x_0=0\) to rozwiązaniem jest \(x(s)=0\), ale dowolnie małe zaburzenie powoduje, że układ „wyskoczy” z tego stanu i zacznie ewoluować do stanu \(x=1\).
Powyższe równanie Verhulsta można rozwiązań analitycznie metodą separacji zmiennych:
Następnie całkujemy obustronnie:
Końcowa postać rozwiązania to funkcja
Jeżeli \(x_0=0\) to \(x(s)=0\). Jeżeli \(x_0 \gt 0\) to \(x(s)\) dąży do stanu stacjonarnego \(x_2=1\).
Chcemy teraz powrócić do „starych” zmiennych \(N=N(t)\) oraz czasu \(t\). Wstawiając \(x=N/K\) oraz \(s=rt\) otrzymamy
Stabilnym stanem stacjonarnym jest stan \(x=1\) czyli \(N=K\). Jest to charakterystyczna liczba osobników jaka ustala się po długim czasie. W modelu Verhulsta obserwujemy nie eksponencjalny wzrost populacji, ale efekt nasycenia: przy danej dostępności populacji do pożywienia, ustala się stabilna liczba osobników w populacji. Wynosi ona \(K\), czyli tyle co parametr \(K\) w równaniu Verhulsta. Dlatego też model ten wydaje się być bardziej zbliżony do realnych warunków.
Na wykresie pokazano 3 charakterystyczne krzywe w zależności od warunku początkowego:
\((A) \quad N_0 \in(0, K/2), \quad \quad N(t) \quad\mbox{jest funkcją rosnącą do wartości K}\)
\((B) \quad N_0 \in [K/2, K), \quad \quad N(t) \quad\mbox{jest funkcją rosnącą do wartości K}\)
\((C) \quad N_0 \gt K, \quad \quad \quad \quad N(t) \quad \mbox{jest funkcją malejącą do wartości K}\)
W przypadku (A), krzywa ma kształt zdeformowanej litery S i dlatego nazywana jest czasami funkcją sigmoidalną (z j. ang. sigmoid function), popularna w zagadnieniach sztucznej inteligencji i sieciach neuronowych.
Poeksperymentuj z Sage!
Rozwiązanie rówania Velhulsta można otrzymać stosując system algebry komputerowej. Sage ma trochę problemów z uzyskaniem postaci jawnej rozwiązania (tzn. \(x(t)=...\)), ale pomaga wykonanie radykalnego uproszczenia - full_simplify() na równaniu.
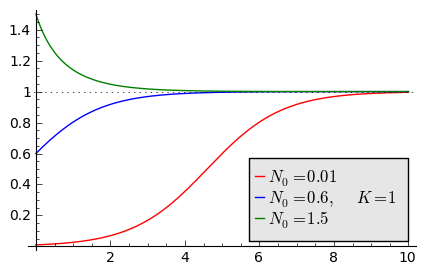
Ewolucja czasowa populacji w modelu Verhulsta dla różnych warunków początkowych
sage: var('n1, n2, n3, t, T4')
sage: T4 = srange(0,3,0.01) ## uwaga: K=1
sage: n1= 0.01*exp(t)/(1+0.01*(exp(t)-1))
sage: n2= 0.6*exp(t)/(1+0.6*(exp(t)-1))
sage: n3= 1.5*exp(t)/(1+1.5*(exp(t)-1))
sage: p10=plot(n1,(t,0,10),figsize=(5,3),color='red', legend_label="$N_0=0.01$")
sage: p20=plot(n2,(t,0,10),color='blue',legend_label="$N_0=0.6, \quad K=1$")
sage: p30=plot(n3,(t,0,10),color='green',legend_label="$N_0=1.5$",gridlines=[[],[1]])
sage: show(p10+p20+p30)
Uogólnienia modelu Verhulsta¶
(A) Model z funkcją Hilla (model Ludwiga)
W modelu Verhulsta uwzględnia się pośrednio naturalny proces śmierci poprzez wartości parametru \(r \gt 0\). Ale jest to sytuacja, gdy w modelu Malthusa \(a \gt b\), czyli tempo urodzin jest większe od tempa śmierci. Model ten można uogólnić na przypadek obecności drapieżników, które zjadają osobników rozważanej populacji. Ponieważ w procesie tym liczba osobników maleje wskutek śmierci spowodowanej przez drapieżników, to w równaniu Verhulsta odzwierciedla to wyraz ujemny \(F(N)\):
Funkcja \(F(N)\) opisująca malenie populacji wskutek istnienia drapieżników powinna spełniać następujące warunki:
\(F(N=0)=0\) - oznacza to tyle, że drapieżnik nie ma co zjadać gdy populacja jest zerowa, N=0.
dla dużych wartości N, funkcja \(F(N)\) powinna się nasycać, to znaczy dążyć do stałej wartości gdy \(N\to \infty\). Oznacza to tyle, że drapieżnik może zjeść pewną maksymalną ale skończoną liczbę ofiar.
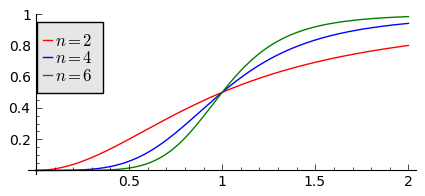
Gdy populacja jest zbyt mała, drapieżnik woli zmienić teren i poszukać populację o większej liczbie osobników. W modelowaniu stosuje się funkcję Hilla, znaną z kinetyki reakcji chemicznych w procesie transkrypcji (proces syntezy RNA na matrycy DNA przez różne polimerazy RNA, czyli przepisywanie informacji zawartej w DNA na RNA). Ma ona postać:
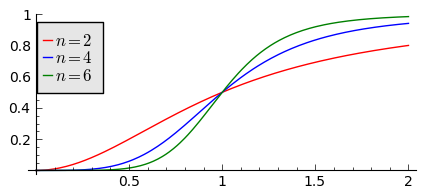
Poniżej pokazujemy jej kształt dla 3 wartości wykładnika \(n=2, 4, 6.\) Przypadek \(n=2\) był zastosowany do opisu populacji motyli z rodziny zwójkowatych (Choristoneura occidentalis), które należą do największych szkodników lasów amerykańskich i kanadyjskich. Model ten, czasami nazywany modelem Ludwiga , sformułowany jest przez równanie:
Powyższe równanie i jego modyfikacje był i jest stosowany do opisu różnorakich procesów: populacji motyli zjadanych przez ptaki, kinetyki reakcji chemicznych, rozwoju komórek nowotworowych, itp. Model ten wykazuje interesujące własności: mogą istnieć 3 stany stacjonarne, ale możliwe są także 2 stany stacjonarne i wreszcie może istnieć tylko 1 stan stacjonarny. Pojawiają się bifurkacje klina i nieciągłe przejścia fazowe. Dokładna analiza tego modelu jest przedstawiona na stronie internetowej iCSE: Przykład użycia metod iCSE: Zagadnienie wzrostu komórki rakowej (https://sage2.icse.us.edu.pl/home/pub/184/)
Funkcja Hilla dla 3 wartości wykładnika n.
sage: var('F1, F2, F3, N, T5')
sage: T5 = srange(0,3,0.01) ## uwaga: A=B=1
sage: F1= N^2/(1+N^2)
sage: F2= N^4/(1+N^4)
sage: F3= N^6/(1+N^6)
sage: pl1=plot(F1,(N,0,2),figsize=(5,2),color='red', legend_label="$n=2$")
sage: pl2=plot(F2,(N,0,2),color='blue',legend_label="$n=4$")
sage: pl3=plot(F3,(N,0,2),color='green',legend_label="$n=6$")
sage: show(pl1+pl2+pl3)
sage: var('F1, F2, F3, N, T5')
sage: T5 = srange(0,3,0.01) ## uwaga: A=B=1
sage: plts = []
sage: c = ['red','blue','green']
sage: for i,n in enumerate([2,4,6]):
... F1= N^n/(1+N^n)
... plts.append( plot(F1,(N,0,2),figsize=(5,2),color=c[i%3], legend_label="$n=%d$"%n) )
sage: show(sum(plts))
(B) Model opisujący efekt Alleego
W 1931 r. W.C. Allee sformułował koncepcję wskazującą na istnienie drugiego stabilnego stanu stacjonarnego, różnego od stanu stacjonarnego N=K w modelu Verhulsta. Allee wykazał, że przy niskich liczebnościach i zagęszczeniach spada przyrost populacji. Mniejsze populacje są bardziej podatne na wymieranie (trudności w znalezieniu partnera, zmniejszona zdolność do grupowej obrony przed drapieżnikami, obniżona wydajność żerowania w grupie). Zgodnie z modelem Verhulsta wzrost populacji jest hamowany tym silniej im bardziej populacja zbliża się do stanu stacjonarnego N=K . Allee wykazał, ze istnieje drugi punkt stacjonarny, który populacja osiąga podczas spadku liczebności. Populacje, w których obserwujemy taki efekt, zmniejszają swoją liczebność, jeśli spadnie ona poniżej pewnego progu. Obecnie efekt Alleego oznacza każdy mechanizm, który prowadzi do zależności między liczbą i/lub zagęszczeniem osobników w populacji a średnim dostosowaniem osobnika. Dobrym przykładem jest losowy rozkład płci, który w małej populacji może prowadzić do zmniejszenia średniego dostosowania poprzez mniejsze szanse na trafienie partnera.
Przykładem modelu uwzgledniajacego efekt Alleego jest zmodyfikowane równanie Verhulsta:
gdzie \(0 \lt N_c \lt K\) jest tym drugim stanem stacjonarnym, o którym mówi Allee. Nie jest to jedyna modyfikacja. W literaturze mozna znaleźć inne modele, ale powyższy model jest najprostszy. W modelu tym istnieją 3 stany stacjonarne:
Analiza stabilności:
Otrzymujemy 2 stabilne stany stacjonarne: \(N=0\) oraz \(N=K\). Stan \(N=N_c\) jest stanem niestabilnym.
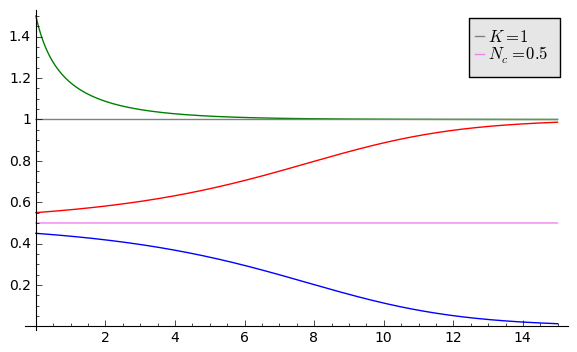
Ewolucja czasowa populacji dla modelu Alleego w zależności od różnych warunków początkowych (dla \(K=1\) oraz \(N_c=0.5\))
sage: var('x,y,z,Z,Y,t')
sage: T0 = srange(0,15,0.01)
sage: f11=x*(x-0.5)*(1-x)
sage: f12=y*(y-0.5)*(1-y)
sage: f13=z*(z-0.5)*(1-z)
sage: f14=0
sage: f15=0
sage: sol5=desolve_odeint( vector([f11, f12, f13, 0, 0]), [0.45,0.55,1.5,0.5,1],T0,[x,y,z,Z,Y])
sage: line( zip ( T0,sol5[:,0]) ,figsize=(7, 4)) +\
... line( zip ( T0,sol5[:,1]) ,color='red')+\
... line( zip ( T0,sol5[:,2]) ,color='green') +\
... line( zip ( T0,sol5[:,4]) ,color='gray',legend_label="$K=1$") +\
... line( zip ( T0,sol5[:,3]) ,color='violet',legend_label="$N_c=0.5$")
Zadania
Można łatwo zmodyfikować powyższy program i analizowac dowolne modele. Dwa poniższe zadania dają przykład możliwości wykorzystania Sage.
Funkcja tempa wzrostu w modelu Verhuslta \(a(N)= r[1-N/K]\) przypomina dwa pierwsze wyrazy w rozwinięciu funkcji eksponencjalnej:
Zbadać własności dynamiki populacji z taką funkcją tempa wzrostu i porównań ze standardowym modelem Verhulsta.
Zbadać własności modelu z funkcją Hilla dla różnych wartości wykładnika \(n = 1, 2, 4, ...\) i porównać je.