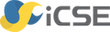Modele oddziałujących populacji: ofiara - drapieżca

Model Lotki-Volterry

W modelu tym rozważamy 2 populacje: populacja zwana „ofiary” i populacja zwana „drapieżniki” lub drapieżcy. Osobniki jednej z nich („ofiary”) są (niestety) zjadane przez osobniki drugiej populacji („drapieżniki”). „Ofiary” mogą rozmnażać się i umierać śmiercią naturalaną. Ponadto „ofiary” giną śmiercią tragiczną zjadane przez „drapieżników”, które to rozmnażają się i umierają śmiercią naturalną (niestety).

Populacja ofiar opisana jest funkcją \(N=N(t)\), natomiast populacja drapieżników opisana jest funkcją \(P=P(t)\). Podobnie jak w modelu Malthusa, tempo zmian w populacji ofiar i drapieżników jest wynikiem urodzin i śmierci w populacji:

\[\frac{dN}{dt} = a N - b N\]

\[\frac{dP}{dt} = c P - e P\]

gdzie parametr \(a\) charakteryzuje tempo urodzin ofiar, \(b\) charakteryzuje tempo śmierci ofiar, \(c\) charakteryzuje tempo urodzin drapieżników i \(e\) charakteryzuje tempo śmierci drapieżników.

Zakładamy, że tempo śmierci ofiar \(b\) zależy od populacji drapieżników: im więcej jest drapieżników \(P\), tym większe jest tempo śmierci ofiar. W prostym opisie oznacza to, że

\[b \to b_0 P\]

gdzie \(b_0\gt 0\) jest parametrem. Podobnie założymy, że tempo urodzin drapieżników \(c\) zależy od populacji ofiar: im więcej jest ofiar \(N\), tym większe jest tempo urodzin drapieżników (im więcej jest pożywienia tym szybciej rozrasta się populacja). Oznacza to, że

\[c \to c_0 N\]

gdzie \(c_0 \gt 0\). Przy takich założeniach model Malthusa zmienia się do postaci

\[\frac{dN}{dt} = a N - b_0 P N\]

\[\frac{dP}{dt} = c_0 N P - e P\]

Wszystkie parametry są dodatnie. Model ten wprowadził w 1926 r. V. Volterra do opisu populacji ryb. Natomiast w 1920 r. A. J. Lotka otrzymał podobne równania do opisu kinetyki autokatalizy (patrz wykład o kinetyce reakcji chemicznych). Stąd model ten nazywa się modelem Lotki-Volterry. W modelu tym pojawiają się 4 parametry. Jak to często bywa, własności tego typu modeli zależą od mniejszej ilości parametrów. Metodą na eliminację niektórych parametrów jest wprowadzenie wielkości bezwymiarowych lub wielkości przeskalowanych. W powyższym przypadku wprowadzimy następujące przeskalowane i bezwymiarowe wielkości:

\[x=\frac{c_0}{e} N, \quad y =\frac{b_0}{a} P\]

oraz bezwymiarowy czas:

\[\tau = a t\]

Po wstawieniu tych wielkości do równań Lotki-Volterry otrzymamy układ równań:

\[\dot x= x- x y\]

\[\dot y = \alpha (xy-y)\]

w którym pojawia się tylko jeden parametr \(\alpha = \frac{e}{a} \gt 0\), który opisuje stosunek tempa śmierci drapieżników \(d\) do tempa urodzin ofiar \(r\). Tak więc procedura przeskalowania równań pozwoliła wyeliminować nieistotne parametry. Jedynym istotnym parametrem jest tylko jeden parametr, a mianowicie \(\alpha\). Własności rozwiązań w modelu Lotki-Volterry zależą tylko od tego parametru i od warunków początkowych \(x(0)\) i \(y(0)\).

STANY STACJONARNE

Stany stacjonarne wyznaczone sa przez równania:

\[f(x, y) = x- x y =0, \quad g(x,y) = \alpha (xy - y) =0,\]

stąd otrzymujemy

\[(x_1=0, y_1=0) \quad \mbox{lub} \quad (x_2=1, y_2 =1)\]

STABILNOŚĆ STANÓW STACJONARNYCH

1. Wyznaczamy macierz Jacobiego

\[\begin{split}J = \begin{bmatrix}\frac{ \partial f}{\partial x}& \frac{\partial f}{\partial y}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial y} \end{bmatrix}\end{split}\]

w punktach stacjonarnych:

\[\begin{split}J_1= J(0, 0) = \begin{bmatrix}1& 0\\ 0& -\alpha \end{bmatrix}, \quad \quad J_2= J(1, 1) = \begin{bmatrix}0& -1\\ \alpha& 0 \end{bmatrix}\end{split}\]

2. Wyznaczamy wartości własne macierzy Jacobiego \(|J-\lambda I|=0\):

1. dla \((0, 0)\) otrzymujemy:

   \(\lambda_{01} = 1,\quad \lambda_{02} =- \alpha\).

   Więc rozwiązanie to nie jest asymptotycznie stabilne, ponieważ jedna z wartości własnych jest dodatnia, tzn. \(\lambda_{01} \gt 0\). Dowolnie małe zaburzenie tego stanu spowoduje ucieczkę układu z tego stanu.

2. dla \((1, 1)\) otrzymujemy:

   \(\lambda_{11} = i \sqrt{\alpha}, \quad \lambda_{12} = -i\sqrt{\alpha}\). Ponieważ wartości własne są urojone, to rozwiązanie jest stabilne, lecz nie jest asymptotycznie stabilne. Dowolnie małe zaburzenie tego stanu spowoduje powstanie stanu, który cały czas będzie w otoczeniu tego stanu \((1, 1)\), ale do niego nie dąży. W pobliżu tego stany, trajektorie są periodyczne i krzywe fazowe powinny być zamknięte.

Znajdziemy teraz postać krzywych fazowych. W tym celu podzielimy obustronnie przeskalowane równania Lotki-Volterry:

\[\frac{dy}{dx}= \frac{\alpha y (x-1)}{x(1-y)}\]

Otrzymliśmy równanie różniczkowe pierwszego rzędu, które rozwiązujemy metodą rozdzielenia zmiennych:

\[\left(\frac{1}{y} - 1\right) \; dy = \alpha \left(1-\frac{1}{x}\right)\; dx\]

Obustronne całkowanie tego równania daje następująca postać krzywych fazowych:

\[\mbox{ln} y -y = \alpha (x- \mbox{ln} x) - H_0\]

gdzie \(H_0\) jest stałą całkowania. Jej wartość określona jest przez warunki początkowe \(x_0\) oraz \(y_0\), ale minimalna wartość jest dla stanu stacjonarnego \((1, 1)\) i wynosi \(H_0 = 1+\alpha\). Poniżej przedstawiamy kilka krzywych fazowych dla różnych wartości \(H_0\). Ponieważ równanie powyższe jest równaniem uwikłanym, jego graficzną wizualizację można bardzo łatwo otrzymać korzystając z SAGE w następujący sposób:

sage: (x,y)=var('x,y') ## alfa=2
sage: p1=implicit_plot(2*x+y -2*ln(x) - ln(y) -5.5, (x,0, 4), (y, 0, 6), color="violet")
sage: p2=implicit_plot(2*x+y -2*ln(x) - ln(y) -5, (x,0, 4), (y, 0, 6), color="red")
sage: p3=implicit_plot(2*x+y -2*ln(x) - ln(y) -4, (x,0, 4), (y, 0, 6), color="green",aspect_ratio=1/2)
sage: show(p1+p2+p3,figsize=5)

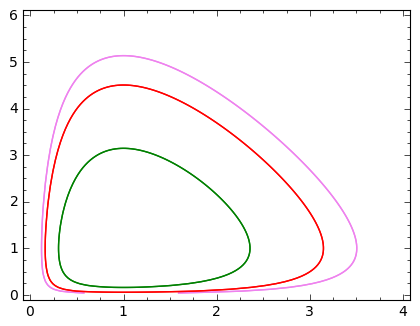
Po pierwsze, zauważamy że krzywe fazowe są zamknięte, więc z tego wynika, że rozwiązania są funkcjami periodycznymi czasu \(t\). Po drugie, zauważamy że wzrost wartości stałej całkowania \(H_0\) powoduje wzrost amplitud oscylacji czasowego przebiegu. Poniżej pokazujemy to explicite rozwiązując numerycznie równania Lotki-Volterry .

Ewolucja czasowa w Modelu Lotki-Volterry

Przebieg czasowy rozwiązań równań Lotki-Volterry można łatwo otrzymać korzystając z pakietu SAGE:

sage: var('x,y') ## warunek początkowy (x0, y0)=(1, 0.3)
sage: a=2
sage: T = srange(0,30,0.01)
sage: sol=desolve_odeint(\
...    vector([x-x*y, a*(x*y-y)]),\
...    [1, 0.3],T,[x,y])
sage: line( zip ( T,sol[:,0]) ,color='green',figsize=(6, 3), legend_label="x")+\
...    line( zip ( T,sol[:,1]) ,color='black',legend_label="y")

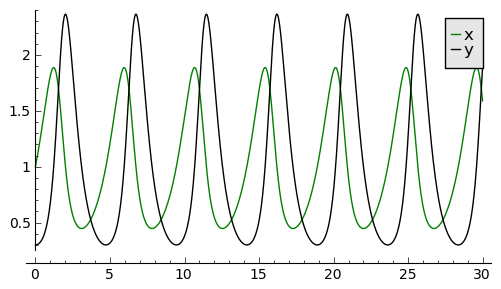
Zauważamy, że maksima w populacji drapieżców pojawiają się później niż maksima w populacji ofiar. Jest to dość jasna własność: drapieżniki mają dużo pożywienia i zjadają ofiary. Łatwy dostęp do pożywienia powoduje szybkie rozmnażanie się drapieżników. Ale to z kolei powoduje, że szybko maleje populacja ofiar i drapieżniki mają utrudniony dostęp do pożywienia i dlatego ich liczba zaczyna maleć. Zmniejszenie się liczby drapieżników powoduje wzrost liczby ofiar. To z kolei powoduje zwiększone zasoby pożywienia dla drapieżników i ich populacja zaczyna wzrastać. I tak powtarza się cykl.

Możemy z powyższych rozwiązań czasowych otrzymać krzywą fazową jako punkty na płaszczyźnie o współrzędnych \((x(t_i), y(t_i))\) zmieniając czas od \(t_i=0\) do jakiegoś \(t_i=t_{max}\). W SAGE wygląda to tak prosto jak poniżej:

sage: list_plot(sol.tolist(), plotjoined=1, figsize=(6, 3))

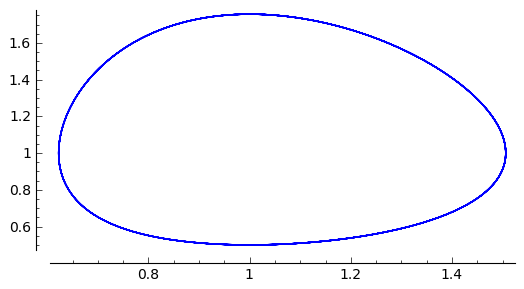
Jak wpływa parametr \(H_0\) na okres oscylacji rozwiązań? Poniżej pokazujemy wpływ warunków początkowych ( tzn. \(H_0\)) na okres oscylacji.

Jeden warunek początkowy to \((1, 0.8) --\gt H1\). Drugi warunek początkowy jest z powyższego przykładu: \((1, 0.3) --\gt H2\).

sage: H1==2*(1-ln(1)) + 0.8 - ln(0.8)

\[H1 == 3.02314355131421\]

sage: H2==2*(1-ln(1)) + 0.3 - ln(0.3)

\[H2 == 3.50397280432594\]

sage: var('x,y')
sage: a=2
sage: T = srange(0,30,0.01)
sage: solu=desolve_odeint(\
...    vector([x-x*y, a*(x*y-y)]),\
...    [1, 0.8],T,[x,y])
sage: line( zip ( T,sol[:,0]) ,color='green',figsize=(6, 3),legend_label="$H_2$")+\
...    line( zip ( T,solu[:,0]) ,color='black',legend_label="$H_1<H_2$")

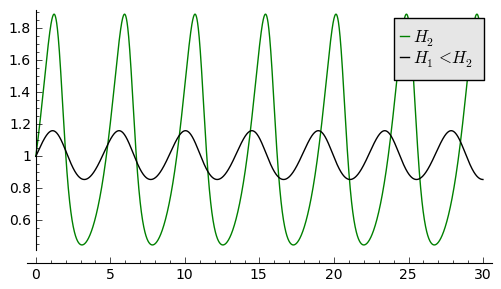
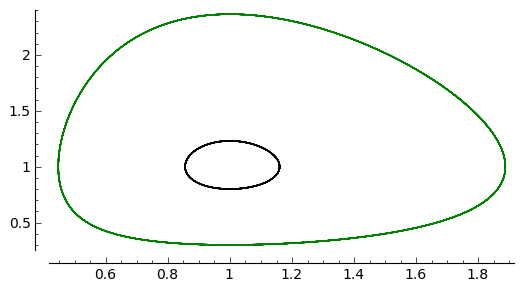
Rozwiązaniom tym odpowiadają krzywe fazowe przedstawione poniżej. Z tych dwóch rysunków wnioskujemy, że gdy \(H_1 \lt H_2\) to amplituda oscylacji jest mniejsza i okres oscylacji jest mniejszy. To odpowiada krzywym fazowym o mniejszym „obwodzie”.

sage: list_plot(sol.tolist(), plotjoined=1,  color='green',figsize=(6, 3))+ list_plot(solu.tolist(), plotjoined=1,  color='black',figsize=(6, 3))

Bardziej realistyczny: Model Maya

W modelu Lotki-Volterry występuje 1 stabilny punkt równowagi: gdy w chwili początkowej przeskalowane populacje \(x_0=1, y_0=1\) to w dowolnej innej chwili, liczba osobników w populacjach nie zmienia się. Natomiast drobne zaburzenia powodują odejście od tego stanu równowagi i pojawiają się oscylacje w obu populacjach. Jeżeli znowu zaburzymy układ, zmienią się także oscylacje, tzn. ich amplituda i ich okres. Często obserwuje się inny rodzaj zachowania. Mimio, że układ zaburza się w niewielkim stopniu, układ powraca do swego poprzedniego stanu. Mówimy, że układ jest strukturalnie stabilny. Tej własności nie posiada model Lotki-Volterry. Przypomnijmy, że model Lotki-Volterry jest w zasadzie 2-wymiarowym modelem Malthusa:

\[\frac{dN}{dt} = a N - b N\]

\[\frac{dP}{dt} = c P - e P\]

w którym procesy rozmnażania i śmierci są modelowane w najprostszy sposób. My mamy jednak doświadczenie nabyte w uogólnianiu modelu Malthusa dla jednej populacji. Możemy teraz to wykorzystać i podobnie zmodyfikować model Lotki-Volterry:

1. w części dla populacji ofiar uwględniamy model Verhulsta i efekty nasycenia z modelu Ludwiga (w funkcją Hilla)

\[a=r\left(1-\frac{N}{K}\right), \quad \quad bN = b_0 \,\frac{N}{D+N} \;P\]

2. w części dla populacji drapieżników uwzględniamy model Verhulsta

\[c = c_0 \left(1-\frac{P}{K_0} \right)\]

Dlatego w drugim równaniu otrzymamy

\[c P - e P = c_0 \left(1-\frac{P}{K_0} \right)\;P - e P = (c_0 - e) P - c_0 \frac{P^2}{K_0} = s P \left(1- \frac{P}{K_1} \right)\]

Zakładamy, że \(s=c_0-e \gt 0\). Przeskalowana stała \(K_1 = K_0 (1-e/c_0).\)

Parametr \(K_1\) modelujący zasoby pożywienia dla drapieżników jest proporcjonalny do liczby osobników ofiar \(K_1=h_0 N\) (\(h_0 \gt 0\) jest stałą proporcjonalności). Więc ostatecznie dostajemy

\[c = s \left(1- h \frac{P}{N}\right)\]

gdzie nowy parametr \(h=1/h_0\).

Uwzględniając powyższe wyrażenia w wyjściowym modelu Malthusa otrzymamy taki oto układ równań:

\[\frac{dN}{dt} = r \left(1-\frac{N}{K}\right) \; N- b_0 \frac{N}{D+N} \; P\]

\[\frac{dP}{dt} = s\left(1-h\frac{P}{N}\right)\; P\]

Wszystkie stałe w tym modelu przyjmują dodatnie wartości. Stałych tych jest aż 6: \(r, K, b_0, D, s, h\). Ile jest istotnych stałych w tym modelu? Musimy umiejętnie dokonać skalowania i wprowadzić wielkości bezwymiarowe. Znowu możemy wykorzystać doświadczenie nabyte w skalowaniu równania Verhulsta, tzn.

\[x= \frac{N}{K}\]

Wstawiając \(N=K x\) to do wyrażenia w nawiasie w równaniu dla \(P\) widzimy że drugą zmienną należy skalować w taki oto sposób:

\[y= h\frac{P}{K}\]

Wówczas otrzymamy:

\[\frac{dx}{d\tau} = (1-x)\, x - \alpha \frac{x y}{d+x}\]

\[\frac{dy}{d\tau} = \beta \left(1- \frac{y}{x}\right) y\]

gdzie zdefiniowaliśmy następujące bezwymiarowe wielkości:

\[\tau = r t, \quad \alpha = \frac{b_0}{h r}, \quad d = \frac{D}{K} , \quad \beta = \frac{s}{r}\]

W wyniku tagiego postepowania otrzymaliśmy układ równań różniczkowych z trzema parametrami. Bezwymiarowy czas skaluje się ze względu na tempo rozmnażania się ofiar. Parametr \(\beta\) to relacja między tempem rozmnażania się drapieżników w stosunku do tempa rozmnażania się ofiar. Jeżeli \(\beta \lt 1\) to tempo rozmnażania się drapieżników jest mniejsze niż tempo rozmnażania sie ofiar i dlatego populacja ofiar może przetrwać. Jeżeli \(\beta \gt 1\) to tempo rozmnażania się drapieżników jest większe niż tempo rozmnażania sie ofiar i dlatego populacja ofiar może wyginąć. Ale ponieważ układ jest nieliniowy, to takie proste dywagacje nie muszą być prawidziwe. Sprawdzimy to dokładniej.

STANY STACJONARNE

Stany stacjonarne są określone przez równania:

\[(1-x)\, x - \alpha \frac{x y}{d+x} = 0\]

\[\beta \left(1- \frac{y}{x}\right) y = 0\]

Jeden stan stacjonarny jest łatwo wyznaczyć:

\[x_0=1, \quad y_0 =0\]

(stan \(x=0\) oczywiście wykluczmy z rozważań, ponieważ gdy nie ma ofiar to i nie ma drapieżników). Powyższy stan to stan bez drapieżników, więc stan stacjonarny populacji ofiar jest taki jak w modelu Verhulsta. Czy ten stan jest stabilny?

Inne stany stacjonarne są określone przez równania:

(1)\[ y=x , \quad \quad (1-x) - \alpha \frac{ y}{d+x} = 0\]

Stąd otrzymujemy równanie dla \(x\) w postaci

\[x^2 + (\alpha + d -1) x -d =0\]

Jest to równanie kwadratowe, ale należy brać pod uwagę tylko dodatnie rozwiązania. Wyróżnik

\[\Delta = (\alpha + d -1)^2 + 4d \gt 0\]

więc otrzymujemy drugi stan stacjonarny

\[x_1= y_1 = \frac{1}{2} \left[- (\alpha + d -1) + \sqrt{\Delta}\right]\]

Zauważmy, że ten stan nie zależy od wartości parametru \(\beta\).

STABILNOŚĆ STANÓW STACJONARNYCH

1. Wyznaczamy macierz Jacobiego

\[\begin{split}\quad \quad \quad J = \begin{bmatrix}\frac{ \partial f}{\partial x}& \frac{\partial f}{\partial y}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial y} \end{bmatrix} = \begin{bmatrix}1-2x-\alpha y \frac{d}{(x+d)^2}& -\alpha \frac{x}{x+d} \\ \frac{\beta y^2}{x^2}& \beta - \frac{2\beta y}{x} \end{bmatrix}\end{split}\]

2. Wyznaczamy wartości własne macierzy Jacobiego \(|J-\lambda I|=0\):

1. dla stanu stacjonarnego \((1, 0)\) otrzymujemy:

\[\begin{split}\quad \quad \quad J(1, 0) = \begin{bmatrix}-1& - \frac{\alpha}{1+d} \\ 0& \beta \end{bmatrix}\end{split}\]

Stąd wartości własne \(\lambda_{1} = -1, \quad \lambda_{2} = \beta\). Więc rozwiązanie to nie jest asymptotycznie stabilne, ponieważ jedna z wartości własnych jest dodatnia, tzn. \(\lambda_{2} \gt 0\). Dowolnie małe zaburzenie tego stanu spowoduje ucieczkę układu z tego stanu.

2. dla drugiego stanu analiza stabilności jest bardziej skomplikowana ponieważ macierz Jacobiego jest postaci

\[\begin{split}\quad \quad \quad J(x_1, y_1) = \begin{bmatrix}x_1\left[ \frac{\alpha x_1}{(x_1+d)^2} -1\right]& - \frac{\alpha x_1}{x_1+d} \\ \beta & -\beta \end{bmatrix}\end{split}\]

Aby otrzymać wyraz \(J_{11}\) tej macierzy, wykorzystaliśmy równanie (1) na stan stacjonarny. Zamiast wyznaczyć wartości własne \((\lambda_{1}, \lambda_{2})\) tej macierzy, wystarczy sprawdzić, kiedy część rzeczywista wartości własnych jest ujemna (lub dodatnia). Ponieważ macierz Jacobiego jest macierzą \(2 \times 2\), więc otrzymujemy równanie kwadratowe dla \(\lambda\). Aby wartości własne miały część rzeczywistą ujemną muszą zachodzić dwie relacje:

\[\lambda_1 + \lambda_2 \lt 0 \quad \mbox{oraz} \quad \lambda_1 \; \lambda_2 \gt 0, \quad \quad \mbox{to oznacza, że} \quad \mbox{Tr} \, J \lt 0, \quad \quad \mbox{det} \,J \gt 0\]

ZADANIE:

Udowodnić, że dla dowolnych (dodatnich) wartości parametrów \(\alpha, \beta, d\), drugi warunek \(\mbox{det} \,J \gt 0\) jest zawsze spełniony.

Pierwszy warunek na stabilność stanu stacjonarnego \((x_1, y_1)\) przyjmuje postać:

\[b \gt x_1\left[ \frac{\alpha x_1}{(x_1+d)^2} -1\right] = \phi (\alpha, d)\]

Ponieważ \(x_1\) zależy od 2 parametrów \(\alpha\) i \(d\), prawa strona przedstawia równanie powierzchni w 3-wymiarowej przestrzeni.

---

sage: var('a b d x y')
sage: ode_lotka=[x*(1-x)-(a*x*y)/(x+d),b*y*(1-y/x)];
sage: show(ode_lotka)

\[\left[-{\left(x - 1\right)} x - \frac{a x y}{d + x}, -{\left(\frac{y}{x} - 1\right)} b y\right]\]

sage: y_z_pierwszego=solve(ode_lotka[0],y,solution_dict=True)[0]
sage: drugie=ode_lotka[1].subs(y_z_pierwszego)
sage: show(drugie)
sage: show(solve(drugie,x,solution_dict=True)[0])
sage: x_0=x.subs(solve(drugie,x,solution_dict=True)[1])
sage: y_0=y_z_pierwszego[y].subs({x:x_0}).expand()
sage: show(x_0)
sage: show( y_0 )

\[-\frac{{\left(\frac{{\left(d - 1\right)} x + x^{2} - d}{a x} + 1\right)} {\left({\left(d - 1\right)} x + x^{2} - d\right)} b}{a}\]

\[\left\{x : -\frac{1}{2} \, a - \frac{1}{2} \, d - \frac{1}{2} \, \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} + \frac{1}{2}\right\}\]

\[-\frac{1}{2} \, a - \frac{1}{2} \, d + \frac{1}{2} \, \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} + \frac{1}{2}\]

\[-\frac{1}{2} \, a - \frac{1}{2} \, d + \frac{1}{2} \, \sqrt{a^{2} + 2 \, a d + d^{2} - 2 \, a + 2 \, d + 1} + \frac{1}{2}\]

sage: ode_lotka[0].diff(x).show()

\[-\frac{a y}{d + x} + \frac{a x y}{{\left(d + x\right)}^{2}} - 2 \, x + 1\]

sage: JJ=jacobian(ode_lotka,[x,y])
sage: show(JJ)

\[\begin{split}\left(\begin{array}{rr} -\frac{a y}{d + x} + \frac{a x y}{{\left(d + x\right)}^{2}} - 2 \, x + 1 & -\frac{a x}{d + x} \\ \frac{b y^{2}}{x^{2}} & -{\left(\frac{y}{x} - 1\right)} b - \frac{b y}{x} \end{array}\right)\end{split}\]

sage: #mamy x0=y0 ;-)
sage: var('x0')
sage: JJ0=JJ.subs({x:x0,y:x0})

sage: show(JJ0)

\[\begin{split}\left(\begin{array}{rr} -\frac{a x_{0}}{d + x_{0}} + \frac{a x_{0}^{2}}{{\left(d + x_{0}\right)}^{2}} - 2 \, x_{0} + 1 & -\frac{a x_{0}}{d + x_{0}} \\ b & -b \end{array}\right)\end{split}\]

sage: show(JJ0.trace())

\[-\frac{a x_{0}}{d + x_{0}} + \frac{a x_{0}^{2}}{{\left(d + x_{0}\right)}^{2}} - b - 2 \, x_{0} + 1\]

\[b = x_1\left[ \frac{\alpha x_1}{(x_1+d)^2} -1\right]\]

sage: expr_murray = x0*(a*x0/(x0-d)^2-1)
sage: expr_murray.show()

\[{\left(\frac{a x_{0}}{{\left(d - x_{0}\right)}^{2}} - 1\right)} x_{0}\]

sage: show( JJ0.trace().subs({x0:x_0})+b )

\[\begin{split}-\frac{{\left(a + d - \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} - 1\right)} a}{a - d - \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} - 1} \\ + \frac{{\left(a + d - \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} - 1\right)}^{2} a}{{\left(a - d - \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} - 1\right)}^{2}} \\ + a + d - \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1}\end{split}\]

sage: p={a:1.23,d:1.01}
sage: show( JJ0.trace().subs({x0:x_0}).subs(p) )
sage: expr_murray.subs({x0:x_0}).subs(p)

\[\begin{split}-b - 0.404054289657954 \\ 1.35696399470668\end{split}\]

sage: var('a,d')
sage: f(a,d)=(a-sqrt(  (1-a-d)^2+4*d) )*(1+a+d-sqrt((1-a-d)^2+4*d))/(2*a)
sage: show(f)
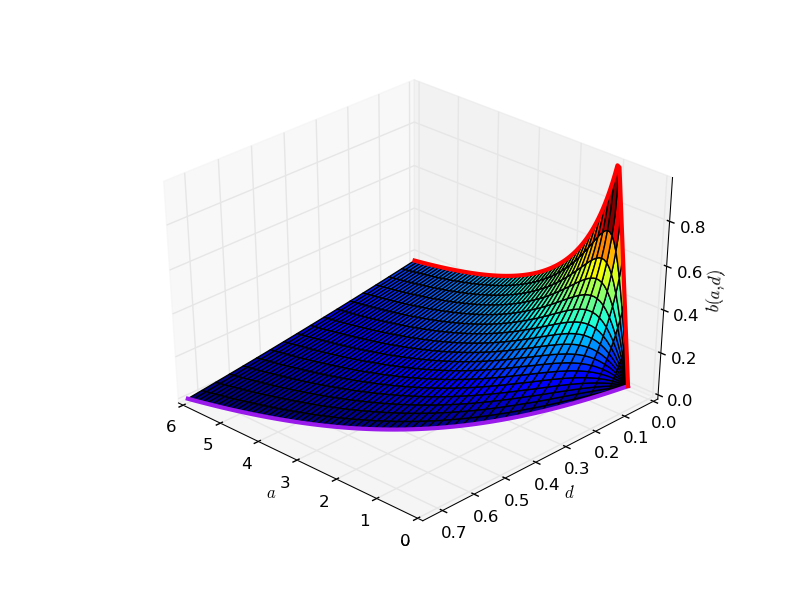
sage: implicit_plot( f(a,d),(d,0,.61),(a,0,2),aspect_ratio=0.3,  figsize=(6, 3), axes_labels=[r'$d$','$a$'] )

\[\left( a, d \right) \ {\mapsto} \ \frac{{\left(a - \sqrt{{\left(a + d - 1\right)}^{2} + 4 \, d}\right)} {\left(a + d - \sqrt{{\left(a + d - 1\right)}^{2} + 4 \, d} + 1\right)}}{2 \, a}\]

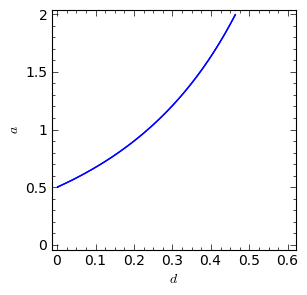
Pod tą płaszczyzną

\[b = x_1\left[ \frac{\alpha x_1}{(x_1+d)^2} -1\right] = \phi (\alpha, d)\]

mamy cykl graniczny:

sage: assume(a>0)
sage: sol1=solve(f(a,d)==0, d)
sage: show(sol1)
sage: dm_expr=sol1[1].rhs()
sage: import sympy
sage: import numpy as np
sage: b2=np.vectorize( sympy.lambdify((a,d), sympy.sympify( f(a,d)  ) ) )
sage: bm=np.vectorize( sympy.lambdify(a,    sympy.sympify( f(a,0)  ) ) )
sage: dm=np.vectorize( sympy.lambdify(a,    sympy.sympify( dm_expr ) ) )
sage: from mpl_toolkits.mplot3d import Axes3D
sage: import matplotlib
sage: from matplotlib import cm
sage: from matplotlib import pyplot as plt
sage: step = 0.04
sage: maxval = 1.0
sage: fig = plt.figure()
sage: ax = fig.add_subplot(111, projection='3d',azim=134)
sage: x = np.linspace(0.5,6,115)
sage: y = np.linspace(0.00,1.,35)
sage: X,Y = np.meshgrid(x,y)
sage: # transform them to cartesian system
sage: X,Y = X,Y*(np.sqrt(X**2+4*X)-(1.0+X))
sage: #Y[:,i((X[7,0]**2+4*X[7,0])**0.5 - (1+X[7,0]) )
sage: #0.99*d(:,i)*((a1.^2+4.*a1)^0.5 - (1+a1) )
sage: Z = b2(X,Y)
sage: ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.jet)
sage: #ax.plot_surface(X, Y, Z,  cmap=cm.jet)
sage: #ax.plot_wireframe(X, Y, Z)
sage: ax.set_zlim3d(0, 1)
sage: ax.set_xlim3d(0, 3)
sage: ax.set_ylim3d(0, .7)
sage: ax.set_xlabel(r'$a$')
sage: ax.set_ylabel(r'$d$')
sage: ax.set_zlabel(r'$b(a,d)$')
sage: ax.plot(x, dm(x), np.zeros_like(x), color=(.6,.1,.92),linewidth=3)
sage: ax.plot(x,np.zeros_like(x), bm(x),  color='red',linewidth=3)
sage: ax.plot([0],[0],[0])
sage: ax.view_init(elev=35, azim=134)
sage: plt.savefig("1.png")

\[\left[d = -\sqrt{a + 4} \sqrt{a} - a - 1, d = \sqrt{a + 4} \sqrt{a} - a - 1, d = -a + \sqrt{2 \, {\left(a + 1\right)} d + a^{2} + d^{2} - 2 \, a + 1} - 1\right]\]

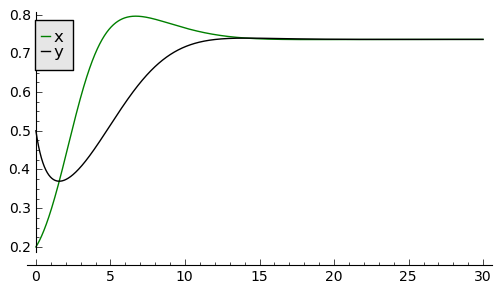
Rozwiązania dążące do stabilnego stanu stacjonarnego: \(a \in (0, 0.5), \beta \gt 0, d \gt 0\)

sage: var('x,y')
sage: a, b, d = 0.3, 0.35, 0.1
sage: T = srange(0,30,0.01)
sage: sol2=desolve_odeint(\
...    vector([x*(1-x) - (a*x*y/(x+d)), b*y*(1-y/x)]),\
...    [0.2, 0.5],T,[x,y])
sage: line( zip ( T,sol2[:,0]) ,color='green', figsize=(6, 3), legend_label="x")+\
...    line( zip ( T,sol2[:,1]) ,color='black',legend_label="y")

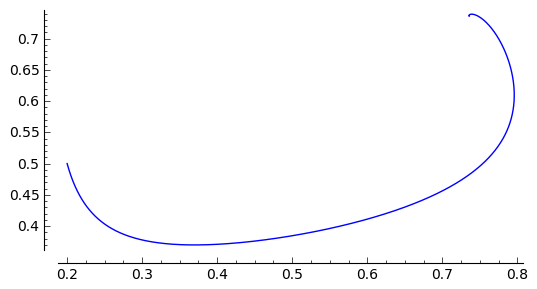
sage: a, b, d = 0.3, 0.35, 0.1
sage: F(x,y)=x*(1-x) - a*x*y/(x+d)
sage: G(x,y)= b*y*(1-y/x)
sage: T = srange(0,30,0.01)
sage: sol1=desolve_odeint(vector([F,G]), [0.2,0.5], T, [x,y])
sage: list_plot(sol1.tolist(), plotjoined=1,  figsize=(6, 3))

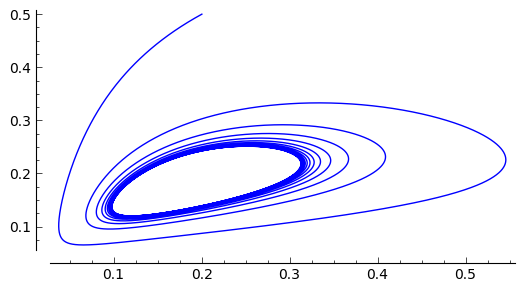
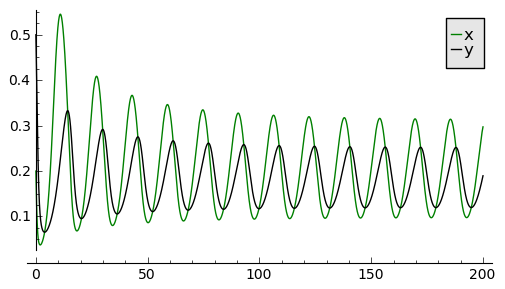
Rozwiązania dążące do stabilnego cyklu granicznego: \(a \gt 0.5 , \beta \gt 0, d \gt 0\)

sage: var('x,y')
sage: a, b, d = 1.3, 0.33, 0.1
sage: T = srange(0,200,0.01)
sage: sol2=desolve_odeint(\
...    vector([x*(1-x) - (a*x*y/(x+d)), b*y*(1-y/x)]),\
...    [0.2, 0.5],T,[x,y])
sage: line( zip ( T,sol2[:,0]) ,color='green', figsize=(6, 3), legend_label="x")+\
...    line( zip ( T,sol2[:,1]) ,color='black',legend_label="y")

sage: a, b, d = 1.3, 0.33, 0.1
sage: F(x,y)=x*(1-x) - a*x*y/(x+d)
sage: G(x,y)= b*y*(1-y/x)
sage: T = srange(0,250,0.01)
sage: sol1=desolve_odeint(vector([F,G]), [0.2,0.5], T, [x,y])
sage: list_plot(sol1.tolist(), plotjoined=1,  figsize=(6, 3))