Równania reakcji-dyfuzji

Dotychczas analizowaliśmy modele dynamiki populacyjnej oraz kinetykę reakcji chemicznych bez uwzględnienia zjawisk rozprzestrzeniania się populacji lub substancji chemicznych na powierzchni czy w przestrzeni. Interesowało nas tylko zachowanie się układu w czasie, a nie w przestrzeni. Oznacza to, że modelowanie oparte było na równaniach różniczkowych zwyczajnych (występują tylko pochodne ze względu na czas) . Uwzględnienie zjawisk związanych z przestrzennymi zmianami modeluje się z pomocą równań różniczkowych cząstkowych (występują pochodne ze względu na zmienne przestrzenne). Poniższy przykład przybliży nam sposób takiego modelowania.

Przykład: zjawisko dyfuzji

Wrzućmy kroplę farby akwarelowej do pojemnika z wodą. Zaobserwujemy, że z upływem czasu cząsteczki farby rozpływają się w coraz to większym obszarze i po odpowiednio długim czasie wypełniaja całkowicie pojemnik z wodą. To, co obserwujemy jest zjawiskiem dyfuzji lub, jak niektórzy nazywają, ruchem cząstek Browna. Jest to zjawisko natury molekularnej, spowodowane nieregularnymi (chaotycznymi) zderzeniami cząsteczek wody i cząsteczek farby. Zauważamy też, że podwyższenie temperatury wody powoduje szybsze mieszanie się obu substancji. W języku fizyki statystycznej oznacza to, że współczynnik dyfuzji ulega zwiększeniu, rosnie natężenie fluktuacji termicznych i następuje przyspieszenie procesu dyfuzji.W języki matematyki, proces ten jest opisany za pomocą równania:

\[\frac{\partial c(\vec r, t)}{\partial t} = D \Delta c(\vec r, t) = D \left[\frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} + \frac{\partial ^2}{\partial z^2} \right] c(\vec r, t)\]

gdzie \(c(\vec r, t)\) jest koncentracją substancji w chwili czasu \(t\) w punkcie przestrzeni określonej przez wektor wodzący \(\vec r = (x, y, z)\). Zwracamy uwagę, że proces dyfuzji jest opisany operatorem Laplace’a (dwukrotnym różniczkowaniem).

Dla początkowej koncentracji \(c(x, y, z, 0)\) skupionej punktowo w początku układu odniesienia \(XYZ\), rozwiązanie równania dyfuzji ma postać

\[c(x, y, z, t) = [4\pi Dt]^{-3/2} \; exp\left[-\frac{x^2+y^2+z^2}{4Dt}\right]\]

Gdyby proces przebiegał tylko w jednym kierunku przestrzennym, np. wzdłuż osi \(OX\) to odpowiednie równanie ma postać

\[\frac{\partial c(x, t)}{\partial t} = D \frac{\partial^2 }{\partial x^2} c(x, t) = D \frac{\partial^2 c(x, t) }{\partial x^2}\]

Jego rozwiązaniem jest funkcja

\[c(x, t) = [4\pi Dt]^{-1/2} \; exp\left[-\frac{x^2}{4Dt}\right]\]

Otrzymujemy więc następującą receptę na uwzględnienie dyfuzyjnego (losowego) rozprzestrzeniania się populacji lub substancji chemicznej:

Do równań opisujących dynamikę populacji dodaj jeszcze wyraz z pochodnymi drugiego rzędu względem zmiennych przestrzennych. Jeżeli zmiany mogą zachodzić tylko w jednym kierunku przestrzennym, to dodajemy wyraz analogiczny jak po prawej stronie powyższego równania. Gdyby zmiany mogły zachodzić na płaszczyżnie, to dodajemy wyraz typu:

\[+ D \left[ \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} \right] c(x, y, t)\]

Rozwiązaniem 2-wymiarowego równania dyfuzji jest funkcja

\[c(x, y, t) = [4\pi Dt]^{-2/2} \; \exp\left[-\frac{x^2+y^2}{4Dt}\right] =\frac{1}{4\pi Dt} \; \exp\left[-\frac{x^2+y^2}{4Dt}\right]\]

sage: def plt_t(t):
...       cmax = c(0,0,t)
...       return contour_plot( c(x,y,t) ,(x,-5,5),(y,-5,5),contours=srange(0.01,cmax,cmax/20.0),cmap='spectral',figsize=(3,3))

sage: times = [.1,0.4,0.9]
sage: html.table([["t=%0.2f"%t for t in times],[plt_t(t) for t in times]])

Wszystkie dotychczas rozważane modele (Malthusa, Verhuslta, autokatalizy, Lotki-Volterry, Maya, Biełousowa-Żabotyńskiego) mogą być uogólnione na przypadek przestrzennych zmian. Dla przykładu, jeżeli równanie dynamiki populacyjnej ma postać

\[\frac{dN(t)}{dt} = F(N(t))\]

to odpowiednie równanie uwzględniające proces dyfuzji ma postać

\[\frac{\partial N(\vec r, t)}{\partial t} = F(N(\vec r, t) ) + D \Delta N(\vec r, t)\]

gdzie w zależności od zagadnienia, laplasjan jest w jednym, dwóch lub trzech wymiarach. Tego typu równanie nazywa się równaniem reakcji-dyfuzji.

Rozważamy poniżej dwa modele: model Malthusa i model Verhulsta.

Model Malthusa z migracją: Równanie Skellama

Standardowy model Malthusa to najprostszy model wzrostu lub zaniku populacji opisany przez równanie różniczkowe

\[\frac{dN(t)}{dt} = k N(t)\]

Jeżeli populacja może przemieszczać się losowo na płaszczyźnie \(XY\) to ogólniona wersja tego równania ma postać

\[\frac{dN(x, y, t)}{dt} = k N(x, y, t) + D \left[ \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} \right] N(x, y, t)\]

gdzie teraz \(N(x, y, t)\) ma interpretację koncentracji populacji (substancji chemicznej) w chwili czasu \(t\) w punkcie o współrzędnych \((x, y)\), czyli liczby osobników na jednostke powierzchni. Jest to jeden z prostszych przykładów układu, który nazywamy równaniem reakcji-dyfuzji. W literaturze, powyższe równanie nazywa się równaniem Skellama, który w 1951 roku zaproponował ten model jako model inwazji gatunku. Zastosował go do opisu inwazji piżmaka w Europie.

http://pl.wikipedia.org/w/index.php?title=Plik:Bisamratte-drawing.jpg&filetimestamp=20041114193425

Do Europy piżmaki sprowadzone zostały na początku XX w. z Ameryki Północnej przez księcia Colloredo-Mansfelda jako zwierzę futerkowe. Cała dzisiejsza europejska populacja dziko żyjących piżmaków pochodzi od kilku osobników, które w 1905 roku uciekły z farmy położonej w Czechach, 40 km na południowy zachód od Pragi. Na ziemiach polskich pojawił się w latach 30. XX w.

W modelu rozpatrujemy tylko takie przypadki że \(N(x, y, t) \ge 0\). Nie jest to jeszcze kompletne sformułowanie problemu. Należy sprecyzować:

1. warunek początkowy \(N(x, y, 0)= N_0(x, y)\)

2. warunki brzegowe

Właściwe warunki brzegowe są często trudne do zdefiniowania. Na pewno na brzegach obszaru koncentracja \(N(\pm \infty, t)\) powinna przyjmować ograniczone wartości. Ale to niekoniecznie musi wystarczać, aby rozwiązania posiadały poprawne własności i były pozbawione artefaktów.

Powyższe równanie reakcji-dyfuzji jest tak trudne (łatwe) do analizy jak równanie dyfuzji. Aby to zobaczyć, dokonamy podstawienia:

\[N(x, y, t)=e^{kt} c(x, y, t)\]

Wstawiając je do równania reakcji-dyfuzji, widzimy że nowa funkcja \(c(x, y, t)\) spełnia równanie

\[\frac{d c(x, y, t)}{dt} = D \left[ \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} \right] c(x, y, t)\]

czyli równanie dyfuzji w dwu-wymiarowej przestrzeni. Rozwiązanie tego równania jest przedstawione powyżej. Więc funkcja \(N(x, y, t)\) ma postać

\[N(x, y, t)=e^{kt} c(x, y, t) = \frac{N_0}{4\pi Dt} \; exp\left[kt -\frac{x^2+y^2}{4Dt}\right]\]

gdzie stała \(N_0=N(0)\) jest liczbą osobników w populacji w chwili początkowej \(t=0\).

Ponieważ koncentracja \(N(x, y, t)\) populacji ma interpretację liczby osobników na jednostkę powierzchni, to

\[\int_{-\infty}^{\;\infty} \;\int_{-\infty}^{\;\infty} N(x, y, t) \,dx \,dy = N(t) = N(0) e^{kt}\]

Zauważmy, że ewolucja koncentracji populacji zależy tylko od położenia w taki oto sposób

\[N(x, y, t)= N(r ,t) = \frac{N_0}{4\pi Dt} \; exp\left[kt -\frac{r^2}{4Dt}\right]\]

gdzie

\[r^2=x^2+y^2\]

jest miarą odległości od początku układu odniesienia.

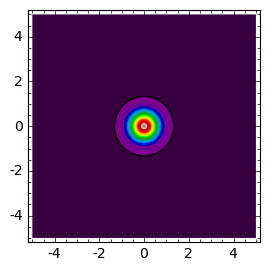
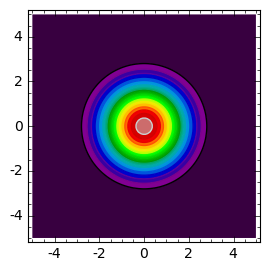
Analizę własności \(N(r, t)\) można łatwo przeprowadzić korzystając z możliwości Sage. Są one przedstawione graficznie poniżej.

Obserwujemy następującą ewolucję populacji:

1. W pewnej umownej chwili początkowej rozkład populacji ma określoną formę (powyżej: dla t=0.1).

2. Wraz z upływem czasu populacja rozprzestrzenia się i jej koncentracja wokół \(r=0\) (w otoczeniu wyjściowego największego skupiska) zaczyna maleć: osobniki rozchodzą się, tempo urodzin jest na razie niewielkie.

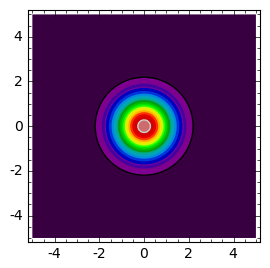
3. Po pewnym czasie koncentracja wokół \(r=0\) przyjmuje minimalną wielkość, a następnie wraz z upływem czasu zaczyna wzrastać (narasta tempo urodzin). Jednocześnie populacja rozprzestrzenia się zajmując coraz to większy obszar.

4. Następnie obserwujemy, że istnieje taka chwila czasu, gdy koncentracja wokół położenia \(r=0\) przekracza wartość początkową i dalej wzrasta w coraz to większym tempie, jednocześnie rozprzestrzeniając się na coraz to większym obszarze. Obserwujemy inwazję populacji. Dalej jest już jak w kiepskim horrorze. Tym nie mniej, scenariusz ten wydaje się dość rozsądny i w pewnych warunkach całkiem dobrze opisuje w ograniczonym przedziale czasowym inwazję populacji.

Pełniejsza analiza tego modelu jest przedstawiona w książce:

Nanako Shigesada and Kohkichi Kawasaki, Biological Invasion: Theory and Practice (Oxford University Press, 2001)

Model Verhulsta z migracją: Równanie Fishera-Kołmogorowa

Model Verhulsta opisuje ewolucję populacji w przypadku ograniczonych zasobów pożywienia w środowisku, w którym żyje dana populacja:

\[\frac{dn(t)}{dt} = r n(t) \; [1- n(t)]\]

gdzie przeskalowana koncentracja \(n(t) = N(t)/K\) i parametr \(K\) nazywa sie pojemnością środowiska.

Model ten opisuje też kinetykę dwóch reakcji autokatalitycznych:

\[A + X {\Longleftrightarrow} 2X , \quad \quad \mbox{lub reakcji} \quad A+X {\Longleftrightarrow} 2X, \quad B+X \rightarrow C\]

Jeżeli uwzględnimy proces rozprzestrzeniania się dyfuzyjnego, model ten przyjmuje postać

\[\frac{\partial n(\vec r, t)}{\partial t} = r n(\vec r, t) \;[1- n(\vec r, t)] + D \Delta n(\vec r, t)\]

W przypadku dynamiki populacyjnej, powinniśmy rozważać migrację na płaszczyżnie (laplasjan w dwóch wymiarach), a w przypadku substancji chemicznych - dyfuzję przestrzenną (pełny trójwymiarowy laplasjan). Oba realistyczne przypadki są wyjątkowo skomplikowane. Dlatego upraszczamy model i redukujemy zagadnienia do przypadku jednowymiarowej dyfuzji i poniżej rozważamy następujące równanie

\[\frac{\partial n(x, t)}{\partial t} = r n(x, t) \;[1- n(x, t)] + D \frac{\partial^2 n(x, t)}{\partial x^2}\]

Równanie to nazywa się równaniem Fishera-Kołmogorowa.

Jak zwykle w modelu tym rozpatrujemy tylko takie przypadki że \(n(x, t) \ge 0\). Należy jeszcze zadać:

1. rozkład początkowy populacji \(n(x, t= 0)= n_0(x)\)

2. warunki brzegowe dla \(n(\pm\infty, t)\)

Warunki brzegowe sformułujemy później.

Analiza równania Fishera-Kołmogorowa

1. Zauważmy, że funkcje stałe \(n(x,t) = n_{0} = 0\) oraz \(n(x, t) = n_{1} = 1\) są rozwiązanami tego równania. Są to te same stany stacjonarne, które są obecne w przypadku modelu Verhulsta bez dyfuzji.

2. Równanie powyższe można przeskalować w następujący sposób:

\[\tau = rt, \quad \quad y^2=\frac{r}{D} x^2, \quad \quad n(x,t) \equiv c(y, \tau)\]

Przeskalowana koncentracja spełnia równanie

\[\frac{\partial c }{\partial \tau} = c [1- c ] + \frac{\partial^2 c}{\partial y^2}, \quad \quad c=c(y, \tau)\]

Funkcje \(c=0\) oraz \(c=1\) są rozwiązaniami stacjonarnymi.

3. Szukamy rozwiązań w postaci fali biegnącej:

\[c(y, \tau) = U(z), \quad \mbox{gdzie } \quad z=y-v_0 \tau\]

Oznacza to, że fala przesuwa się w prawo z prędkością \(v_0\). Często mówi się, że front falowy koncentracji porusza się w prawo z prędkością \(v_0\).

Zauważamy, że

\[\frac{\partial c }{\partial \tau} = \frac{\partial U}{\partial \tau} = \frac{d U}{d z} \frac{\partial z}{\partial \tau} = -v_0 \frac{d U}{d z}\]

\[\frac{\partial c }{\partial y} = \frac{\partial U }{\partial y} = \frac{d U }{d z} \frac{\partial z }{\partial y} = \frac{d U }{d z}\]

\[\frac{\partial ^2 c }{\partial y^2} = \frac{\partial^2 U }{\partial y^2} = \frac{d ^2U }{d z^2}\]

Stąd, nowa funkcja \(U(z)\) spełnia równanie różniczkowe zwyczajne drugiego rzędu:

\[U'' + v_0 U' + U(1-U)=0\]

Jest ono równoważne układowi 2 równań:

\[U'=V = F(U, V), \quad \quad V'=-v_0 - U(1-U) = G(U, V)\]

Stany stacjonarne określone są przez pierwiastki równań:

\[F(U, V) = 0, \quad \quad G(U, V) = 0,\]

stąd otrzymujemy 2 par rozwiązań

\[(U_0, V_0) = (0, 0), \quad (U_1, V_1) = (1, 0)\]

1. Wyznaczamy macierz Jacobiego

\[\begin{split}\quad \quad \quad \quad J = \begin{bmatrix}\frac{ \partial F}{\partial U}& \frac{\partial F}{\partial V}\\ \frac{\partial G}{\partial U}& \frac{\partial Gg}{\partial V} \end{bmatrix}= \begin{bmatrix}0, & 1\\ -1+2U, & -v_0 \end{bmatrix}\end{split}\]

w punktach stacjonarnych:

\[\begin{split}J_0= J(0, 0) = \begin{bmatrix}0& 1\\ -1& -v_0 \end{bmatrix}, \quad \quad J_1= J(1, ) = \begin{bmatrix}0& 1\\ 1& -v_0 \end{bmatrix}\end{split}\]

2. Wyznaczamy wartości własne macierzy Jacobiego \(|J-\lambda I|=0\):

1. dla \((0, 0)\) otrzymujemy:

\[\lambda_{\pm}(0, 0) = (1/2)[-v_0\pm\sqrt{v_0^2-4}]\]

Należy rozważyć 2 przypadki: \(v_0 \lt 2\) oraz \(v_0 \ge 2\). Pierwszy przypadek należy odrzucić, ponieważ wartości własne są zespolone, o rzeczywistej części ujemnej i krzywe fazowe tworzą spiralę wokół punktu \((0, 0)\). Ale to oznacza, że \(U\) przyjmuje także ujemne wartości, co nie jest dopuszczalne (koncentracje populacji mogą być tylko dodatnie lub zerowe). Pozostaje tylko drugi przypadek:

\[v_0 \ge 2\]

2. dla \((1, 0)\) otrzymujemy: \(\lambda_{\pm}(1, 0) = (1/2)[-v_0\pm\sqrt{v_0^2+4}]\). Ponieważ jedna z wartości własnych jest dodatnia, ten stan stacjonarny jest niestabilny (jest to stan stacjonarny typu siodło).

sage: F(u,v)=v
sage: G(u,v)= -2*v-u+u^2 #ewolucja z  otoczenia stanu stacjonarnego (1,0)
sage: T1 = srange(0,5,0.01) #druga liczba=ilość iteracji="czas"
sage: T2 = srange(0,29,0.01)
sage: solo2=desolve_odeint(vector([F,G]), [0.8, 0.01], T1, [u,v]) # warunek pocz (U, V)
sage: solo3=desolve_odeint(vector([F,G]), [0.999, 0], T2, [u,v]) # warunek pocz (U, V)
sage: list_plot(solo2.tolist(), plotjoined=1, color='green', figsize=(7,3)) + list_plot(solo3.tolist(), plotjoined=1, figsize=(7,3))

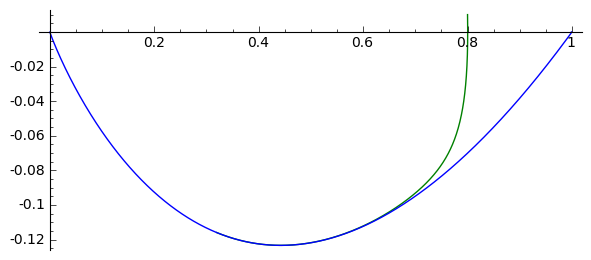
Zauważmy, że istnieją stany początkowe z otoczenia stanu \((1, 0)\), które dążą do stanu \((0, 0)\). Innymi słowy funkcja \(U(z)\) z otoczenia \(U(z) \approx 1\) łączy się z funkcją \(U(z)=0\). To sugeruje wybór warunków brzegowych w postaci:

\[\lim_{z\to -\infty} U(z) = 1, \quad \quad \lim_{z\to \infty} U(z) = 0\]

Pamiętając o własnościach stanów stacjonarnych w standardowym modelu Verhulsta (\(n(t) \to 1\) dla \(t\to \infty\)), oznacza to, że dla ustalonej wartości położenia \(y\):

\[\lim_{z\to -\infty} U(z) = \lim_{\tau \to \infty} U(y-v_0 \tau ) = \lim_{\tau \to \infty} c(y, \tau ) = 1\]

co jest konsystentne z zachowaniem się układu w przypadku bez migracji.

Dokładne rozwiązanie w szczególnym przypadku

Istnieje jeden szczególny przypadek, gdy znane jest dokładne rozwiązanie równania Fishera-Kołmogorowa w postaci analitycznej. Dal prędkości fali

\[v_0 = \frac{5}{\sqrt{6}}\]

rozwiązanie ma postać:

\[c(y, \tau) = \frac{1}{\left\{1+A \exp\left[ (y-v_0 \tau)/\sqrt{6}\right] \right\}^{2}}\]

gdzie stała \(A\gt 0\) określa początkowy profil koncentracji.

Analiza numeryczna równania Fishera-Kołmogorowa:

\[\frac{\partial n(x, t)}{\partial t} = r n(x, t) \;[1- n(x, t)] + D \frac{\partial^2 n(x, t)}{\partial x^2}\]

Przyjęto okresowe warunki brzegowe, poprzez odpowiedni wybór dyskretnego operatowa dyfuzji \(L\). Najpierw wybieramy dyskretyzację przestrzeni, potem dobieramy maksymalny krok czasowy tak by warunek CFL był spełniony.

Aby uzyskac rozwiązanie z wyraźną falą biegnącą należy wziąć dla \(r=0\) wartości dyfuzji poniżej \(D\lt 0.001\). Dla większych wartości stałych dyfuzji najpierw nastąpi wyrównanie poziomu \(u\) na obszarze, a potem wzrost do wartości stabilnej \(u=1\).

Długość układu wchodzi efektywnie w skalowanie stałej dyfuzji, można więc bez straty ogólności rozważać układy o długości 1.

\[u^{i+1} = u^i + dt \left( r u^i (1-u^i) + D \frac{1}{h^2} Lu^i\right),\]

gdzie \(L\) jest dyskretnym operatorem Laplace’a.

Ponieważ część nieliniowa jest lokalna (nie zawiera pochodnych), to warunki brzegowe są zawarte w operatorze \(L\).

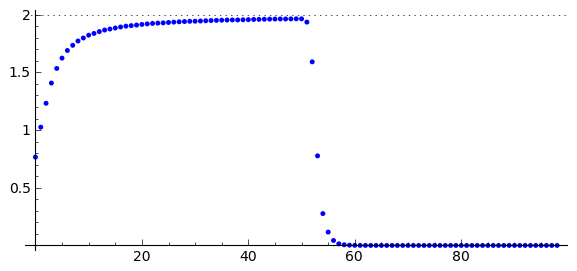
Prędkość frontu fali:

sage: pos_lst = []
sage: for T_ in Tlst:
...       for (i,a),b in zip(enumerate(T_),T_[1:]):
...           if a>=0.5 and b<=0.5:
...               pos_lst.append( i+(a-0.5)/(a-b) )
...
sage: list_plot( [l/(N-1)*(b-a)/(sps*dt) for a,b in zip(pos_lst,pos_lst[1:])] , figsize=(7,3),gridlines=[[],[2]],ymax=2)