Modele epidemii

Model Kermacka-McKendricka

W języku potocznym termin epidemia używany jest jako synonim masowych zachorowań wywołanych chorobami zakaźnymi. Często definiuje się ją jako wystąpienie na danym obszarze zakażeń lub zachorowań na chorobę zakaźną w liczbie wyraźnie większej niż we wcześniejszym okresie albo wystąpienie zakażeń lub chorób zakaźnych dotychczas niewystępujących. Przypadki globalnych epidemii nazywa się pandemią. Oto kilka przykładów epidemii (pandemii):

• grypy

• grypa hiszpanka (1918-1919) – ponad 50 mln ofiar śmiertelnych na całym świecie

• grypa azjatycka (1957) – ok. 1 mln ofiar śmiertelnych na całym świecie

• grypa Hong-Kong (1968) – ok. 1 mln ofiar śmiertelnych na całym świecie

• Pandemia grypy A/H1N1 (od 11 czerwca 2009) - ok. 12799 ofiar na całym świecie

• AIDS – masowe zachorowania; zwłaszcza na kontynencie afrykańskim

Jak zwykle zaczniemy modelowanie epidemii jakiejś choroby od uproszczających założeń. Rozważamy izolowaną populację, a w niej 3 grupy osób:

1. osoby podatne, które mogą zachorować; ich populacje oznaczamy przez \(S\)

2. ososby chore (zainfekowane) \(I\) oraz

3. osoby, które wyzdrowiały i są odporne na nową infekcję \(R\).

W punkcie 3 zakłada się, że choroba jest wyleczalna i nie prowadzi do śmierci. Równie dobrze można założyć, że choroba jest całkowicie śmiertelna i wówczas \(R\) jest liczbą osób matrwych z powodu choroby.

Ponieważ jest to populacja izolowana, więc całkowita liczba wszystkich osobników jest stała

\[S + I + R = N_0 = const.\]

Zmiana liczebności osobników w poszczególnych grupach jest wyznaczona przez równania:

\[\frac{dS}{dt} = - r S I, \quad \quad \frac{dI}{dt} = r S I -aI, \quad \quad \frac{dR}{dt} = aI\]

Równania te mają podobną strukturę jak równania dynamiki populacyjnej Lotki-Volterry. Uzasadnienie tych równań jest podobne:

1. Liczba osobników w grupie podatnych \(S\) maleje (pochodna jest ujemna), ponieważ mogą zachorować. Tempo ubytku osobników \(S\) zależy od liczby osób chorych \(I\), ponieważ im więcej jest nosicieli choroby, tym więcej ludzi może być zainfekowanych.

2. Liczba osób chorych \(I\) zmienia się z dwóch powodów. Pierwszy powód: \(I\) wzrasta (wyraz po prawej stronie równania jest dodatni) ponieważ nowe osoby są infekowane. Drugi powód: \(I\) maleje (wyraz po prawej stronie jest ujemny) ponieważ chorzy zdrowieją.

3. Osób ozdrowiałych \(R\) (lub martwych) przybywa (pochodna jest dodatnia).

Jeżeli dodamy obustronnie do siebie wszystkie 3 równania, to wyrazy po prawej stronie uproszczą się i otrzymamy zero:

\[\begin{split}\frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} = \frac{d(S + I + R)}{dt} = 0 \quad \quad \Rightarrow \quad \quad S + I + R = const. \quad \quad \Rightarrow \\ S(t) + I(t) + R(t) = const. = S(0) + I(0) + R(0) = N_0\end{split}\]

Jak widać, całkowita liczba osobników \(S(t) + I(t) + R(t)\) w populacji nie zmienia się w czasie i jest określona przez \(S(0) + I(0) + R(0)\) w początkowej chwili czasu. Więc równania ewolucji są zgodne z założeniem o wyizolowanej populacji. Powyższy model można modyfikować na wiele sposobów. Po wykładach o modelowaniu dynamiki populacyjnej, każdy student może stworzyć swój model i badać jego własności.

Zbadajmy własności proponowanego modelu, który nazywa się modelem Kermacka-McKendricka. Będziemy uważali, że model ten może opisywać zjawisko epidemi, jeżeli w trakcie ewolucji czasowej liczba osób chorych \(S(t)\) będzie funkcją rosnącą od danej chwili zwanej umownie chwilą początkową (czasem początkowym) \(t_0 = 0\). Nie będziemy wymagać, aby w zjawisku epidemii \(S(t)\) była cały czas funkcją rosnącą. Po pewnym czasie, epidemia może być opanowana i wówczas \(S(t)\) zacznie maleć. Jeżeli z kolei \(S(t)\) będzie funkcją malejącą już od chwili początkowej \(t_0 = 0\), nie będzie to zjawisko epidemii.

Dwa pierwsze równania tworzą zamknięty i niezależny układ równań różniczkowych:

\[\frac{dS}{dt} = - r S I, \quad \quad \frac{dI}{dt} = r S I -aI = I (r S - a)\]

Możemy zastosować dobrze znaną nam metodę badania stanów stacjonarnych i ich stabilności. Przyrównując prawe strony do zera otrzymamy możliwe stany stacjonarne:

\[I = 0 \quad \quad \quad S = \frac{a}{r}\]

Obliczmy odpowiednią macierz Jacobiego:

\[\begin{split}\quad \quad \quad \quad J (S, I) = \begin{bmatrix}-r I& -r S\\ r I & r S - a \end{bmatrix} \quad \quad \mbox{w punkcie stacjonarnym:} \quad J= J(a/r, 0) = \begin{bmatrix}0&-a\\ 0&0 \end{bmatrix}\end{split}\]

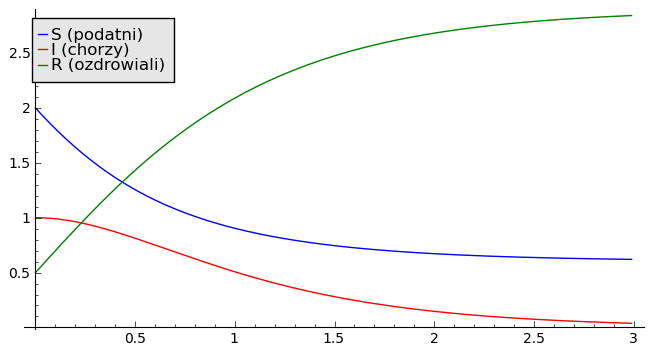
Wyznaczamy wartości własne macierzy Jacobiego \(|J-\lambda I|=0\). Prosty rachunek pokazuje, że wartości własne wynoszą zero. Więc analiza liniowa stabilności nie może być stosowana!! Należy w inny sposób badać zachowanie sie układu. Wykorzystajmy numeryczną analizę z użyciem SAGE. W modelu występują dwa parametry: tempo infekcji \(r\) oraz tempo zdrowienia \(a\). One powinny decydować o ewolucji rozprzestrzeniania się choroby. Ale to jest za mało. Okazuje się, żę także warunki początkowe odgrywają istotną rolę. Poniżej przedstawiamy dwa zestawy parametrów \(r\) oraz \(a\) przy ustalonych i tych samych warunkach początkowych.

Przykładowy zestaw parametrów

Dwa parametry: tempo infekcji \(r\) oraz tempo zdrowienia \(a\) decydują o początkowej ewolucji rozprzestrzeniania się choroby (przy założeniu ustalonych warunkach początkowych). Jako pierwszy przykład, rozpatrujemy:

\[r \lt a\]

sage: var('S I R') ## w tej części układ równań jest numerycznie rozwiązywany
sage: r,a = 1,2
sage: T = srange(0, 3,0.01)
sage: sol=desolve_odeint( vector([-r*S*I,r*S*I - a*I, a*I]), [2,1,0.5],T,[S,I,R])
sage: line( zip ( T,sol[:,0]) ,figsize=(8,4),legend_label="S (podatni)") +\
...    line( zip ( T,sol[:,1]) ,color='red',legend_label="I (chorzy)")+\
...    line( zip ( T,sol[:,2]) ,color='green',legend_label="R (ozdrowiali)")

Inny zestaw parametrów

Zmieniamy relacje między dwoma parametrami: tempem infekcji \(r\) oraz tempem zdrowienia \(a\):

\[r \gt a\]

sage: var('S I R')
sage: r1,a1 = 4,0.5
sage: T = srange(0,3,0.01)
sage: sol=desolve_odeint( vector([-r1*S*I,r1*S*I - a1*I, a1*I]), [2,1,0.5],T,[S,I,R])
sage: line( zip ( T,sol[:,0]) ,figsize=(8,4),legend_label="S (podatni)") +\
...    line( zip ( T,sol[:,1]) ,color='red',legend_label="I (chorzy)")+\
...    line( zip ( T,sol[:,2]) ,color='green',legend_label="R (ozdrowiali)")

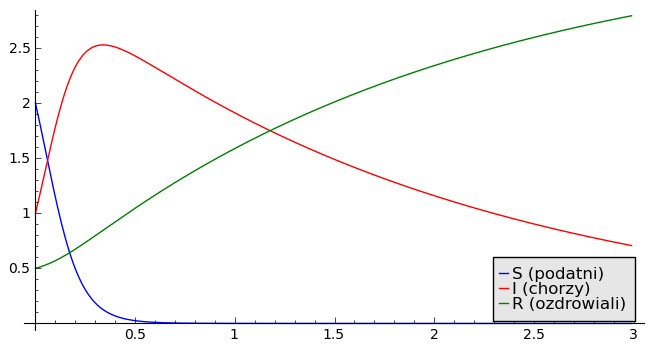
Powyższe 2 zestawy parametrów prowadzą do 2 różnych ewolucji. Dlaczego? Aby rozwikłać ten problem, rozpatrzmy własność równania dla \(I\):

\[\frac{dI}{dt} = r S I -aI = I (r S - a)\]

Początkowa ewolucja zależy od znaku pochodnej dla czasu \(t \to 0\). Dobrze wiemy o tym że jeżeli pochodna jest dodatnia, to funkcja rośnie; jeżeli pochodna jest ujemna to funkcja maleje.

Znak pochodnej w zerze to:

\[\frac{dI}{dt}|_{t=0} = r S(0) I(0) - a I(0) = I(0) [r S(0) - a]\]

Jeżeli \(r S(0) - a \gt 0\) to funkcja \(I(t) \gt I(0)\) rośnie i pojawia się epidemia. Jeżeli \(r S(0) - a \lt 0\) to funkcja \(I(t) \lt I(0)\) maleje i nie pojawia się epidemia. W zagadnieniu tym pojawia się zjawisko progowe. Wartością progową jest wielkość:

\[S_c = \frac{a}{r}\]

Gdy w chwili początkowej \(S(0) \gt S_c\) to pojawia się epidemia!

Pojawienie sie epidemii zależy od tego jak duża jest populacja ludzi podatnych na zakażenie. Populacja ta musi być odpowiednio duża, a jej minimalna wartość zależy od tego jakie jest tempo zdrowienia \(a\) w relacji do tempa infekcji \(r\). To jest najważniejszy wniosek z tej analizy.

Przykład

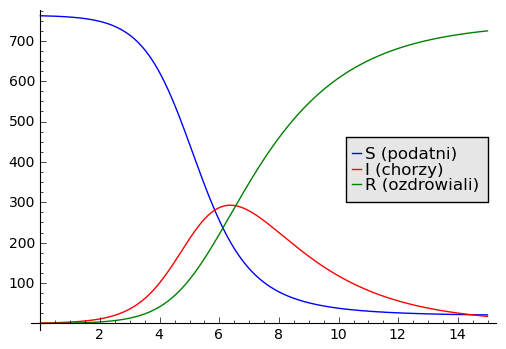
Powyższy model zastosowano do opisu epidemii grypy w 1978 roku w jednej z angielskich szkół dla chłopców (może dlatego tam pojawiła się epidemia?). A oto dane:

Wszystkich uczniów było 763. Jeden z chłopców był chory i zaczął zakażać swoich kolegów. Skutek był taki, że w przeciągu kilku dni (od 22 stycznia do 4 lutego) zachorowało 512 uczniów. W szóstym dniu od pojawienia się choroby epidemia osiągnęła maksimum: było chorych 300 chłopców. W następnych dniach ich liczba zaczęła spadać. Dopasowano krzywą empiryczną do modelu i otrzymano następujące wartości parametrów:

\[r = 0.00218, \quad \quad \quad S_c = 202.\]

Wykreślić wszystkie trzy krzywe.

sage: var('S I R')
sage: r2,s = 0.00218, 202
sage: T = srange(0,15,0.01)
sage: sol=desolve_odeint( vector([-r2*S*I,r2*I*(S - s),r2*s*I]), [762,1,0],T,[S,I,R])
sage: line( zip ( T,sol[:,0]) ,figsize=(6,4),legend_label="S (podatni)") +\
...    line( zip ( T,sol[:,1]) ,color='red',legend_label="I (chorzy)")+\
...    line( zip ( T,sol[:,2]) ,color='green',legend_label="R (ozdrowiali)")

Geograficzne rozprzestrzenianie się epidemii

W poprzednim modelowaniu nie byliśmy zainteresowani czy epidemia choroby rozprzestrzenia się na danym obszarze. Interesowało nas tylko to, czy zachorowalność w czasie wzrasta czy maleje; czy liczba ludzi chorych rośnie czy maleje w czasie. W tej części interesuje nas, w jaki sposób choroba „rozmywa się” się na danym obszarze. Mamy już pewne doświadczenie, aby taki proces modelować. Nabyliśmy je przy modelowaniu modelu Malthusa z migracją i modelu Verhulsta z migracją. Otrzymaliśmy równania, którę w literaturze nazywają się równaniami reakcji-dyfuzji. Podobnie będziemy postępować teraz: do naszych równań Kermacka-McKendricka dodamy wyraz (lub wyrazy) opisujące proces dyfuzji, czyli losowego rozchodzenia się danego zjawiska na określonym obszarze:

\[\frac{\partial S }{\partial t} = -r S I + D_s \Delta S\]

\[\frac{\partial I }{\partial t} = r S I - a I + D \Delta I\]

gdzie \(S = S(\vec r, t)\) oraz \(I = I(\vec r, t)\) opisuje koncentrację populacji w chwili czasu \(t\) w punkcie obszaru określonym przez wektor wodzący \(\vec r = (x, y)\). Parametry \(D_s\) oraz \(D\) są współczynnikami dyfuzji i opisują tempo zmian przestrzennych odpowiednich populacji \(S\) i \(I\). Zwracamy uwagę, że proces dyfuzji jest opisany operatorem Laplace’a (dwukrotnym różniczkowaniem). Na przykład :

\[\Delta S(\vec r, t) = \left[\frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} \right] S (\vec r, t)\]

W przypadku uproszczonych modeli, operator Laplace’a może dotyczyć tylko jednej zmiennej (dyfuzja w jednym wymiarze). Jeżeli nie interesuje nas przestrzenna zmiana osobników podatnych \(S\), wówczas otrzymamy model tego typu:

\[\frac{\partial S }{\partial t} = -r S I\]

\[\frac{\partial I }{\partial t} = r S I - a I + D \Delta I\]

Model tego typu był szeroko stosowany do opisu rozprzestrzeniania się wścielkizny wśród dzikich zwierząt, zwałaszcza wśród populacji lisów. Jeszcze pod koniec lat 60-ych do połowy lat 70-tych XX wieku we Francji wścielkizna stanowiła poważny problem i rozprzestrzeniała się w szybkim tempie z północnej części Francji aż do południowych krańców Francji.

Powyższy model rozszerzono uwzględniając naturalny wzrost populacji lisów wskutek urodzin:

\[\frac{\partial S }{\partial t} = -r S I + B S \left(1-\frac{S}{S_0}\right)\]

\[\frac{\partial I }{\partial t} = r S I - a I + D \Delta I\]

W pierwszym równaniu rozpoznajemy drugi wyraz po prawej stronie opisujący wzrost populacji podatnej populacji \(S\) taki jak w modelu Verhulsta. Parametry \(B\) oraz \(S_0\) mają taką samą interpretację jak w modelu Verhulsta: \(B\) opisuje tempo wzrostu populacji, natomiast \(S_0\) opisuje pojemność środowiska (zasoby pożywienia).

W modelu tym występuje aż 6 parametrów. Odpowiednie skalowanie pozwala zredukować liczbe parametrów. Zawsze jest ciekawym zagadnieniem, od ilu istotnych parametrów zależż własności opisywanego układu. Wprowadźmy następujące wielkości bezwymiarowe:

\[U = \frac{S}{S_0}, \quad \quad V = \frac{r I}{B S_0}, \quad \quad y = \left(\frac{B}{D}\right)^{1/2} x , \quad \quad \tau = B t, \quad \quad \lambda = \frac{a}{r S_0}, \quad \quad \alpha = \frac{r S_0}{B}\]

W nowych zmiennych równania mają postać:

\[\frac{\partial U }{\partial t} = U (1 - U - V)\]

\[\frac{\partial V }{\partial t} = \alpha V ( U - \lambda) + \Delta V\]

Jak widać, jedynie 2 parametry (\(\alpha\) oraz \(\lambda\)) pojawijają się w przeskalowanych równaniach. Jedynie te 2 parametry są istotne dla charakteryzacji własności układu.

Relistyczne modelowanie rozprzestrzeniania się epidemii

Można rozbudować modele o następujące czynnki:

1. Epidemia w ośrodku jednorodnym

2. Epidemia w ośrodku niejednorodnym:

• Przeszkody będące scianką odbijającą dla dyfuzji u i v rozmieszczone w pewien sposób (np. losowy).

• Przeszkody będące źródłem lub zlewem u lub v. Na przykład można sobie wyobrazić, że mamy miejsca w przestrzeni w które usuwają chorych (szpitale).

• Dodanie zmienności różnych stałych od miejsca. Na przykład miejsc w których zachodi zdrowienie chorych z dużą prędkościa dyfuzja chorych jest zero a dyfizja zdrowych duża (Uwaga na modelowanie zmiennej stałej dyfuzji!).

Poniżej zamieszczone są dwa przykłady, w pierszym mamy możliwość dodania źródeł lub zlewów u i v a w drugim zaimplementowana jest złożona geometria z warunkiem von Neumanna.

sage: var('u,v')
sage: T = srange(0,45,0.01)
sage: #sol=desolve_odeint( vector([u*(.0-0.0*u-v),a*v*(u-lam)]), [1,0.1],T,[u,v])
sage: sol=desolve_odeint( vector([-a*u*v,a*v*u-lam*a*v]), [1,0.1],T,[u,v])
sage: uvt = line( zip ( T,sol[:,0]) ,figsize=4,legend_label="S (podatni)") +\
...    line( zip ( T,sol[:,1]) ,color='red',legend_label="I (chorzy)")
sage: html.table([["Przestrzeń fazowa (u,v)","u(t) i v(t)"],[line( sol,figsize=4 ),uvt]])

Model rozprzestrzeniania się epidemii w ośrodku jednorodnym

sage: %timeit
sage: import numpy as np
sage: sparse = True
sage: slicing = True
sage: Dyf_u = .0
sage: Dyf_v = 1.02
sage: Dyf = max(Dyf_u,Dyf_v)
sage: a = 1.0
sage: lam = .3
sage: l = 100.0 # dlugosc ukladu
sage: t_end = 200 # czas symulacji
sage: N = 160 # dyskretyzacja przestrzeni
sage: h = l/(N-1)
sage: dt = 0.052/(Dyf*(N-1)**2/l**2) # 0.2 z warunku CFL, krok nie moze byc wiekszy
sage: dt_dyn = 0.02
sage: print "dt,dt_dyn",dt,dt_dyn
sage: dt = min(dt,dt_dyn)
sage: sps = int(1/dt) # liczba krokow na jednostke czasu
sage: Nsteps=sps*t_end  # calkowita liczba krotkow
sage: print "sps=",sps,"dt=",dt,'Nsteps=',Nsteps
sage: # warunek poczatkowy
sage: u = np.zeros((N,N))
sage: v = np.zeros((N,N))
sage: u[:,:]=1.0
sage: v[50:60:,50:60]=0.1
sage: perc =4100
sage: irand,jrand = np.random.randint(0,u.shape[0],perc),np.random.randint(0,u.shape[0],perc)
sage: def essential_boundary_conditions(u):
...       global irand,jrand
sage: #    u[irand,jrand]=1
sage: #    v[irand,jrand]=0
...       u[:,0] = 1.0
...       u[:,-1] = 1.0
...       u[-1,:] = 1.0
...       u[0,:] = 1.0
...       v[:,0] = 0.0
...       v[:,-1] = 0.0
...       v[-1,:] = 0.0
...       v[0,:] = 0.0
...
sage: Tlst=[]
sage: Tvlst=[]
sage: essential_boundary_conditions(u)
sage: for i in range(Nsteps):
...       if not i%sps:
...           Tlst.append(u.copy())
...           Tvlst.append(v.copy())
...
...       u[1:-1,1:-1] = u[1:-1,1:-1] + dt*(u[1:-1,1:-1]*( 0.0 - 0*u[1:-1,1:-1]-v[1:-1,1:-1] ) + \
...        Dyf_u*(N-1)**2/l**2*(np.diff(u,2,axis=0)[:,1:-1]+np.diff(u,2,axis=1)[1:-1,:]))
...       v[1:-1,1:-1] = v[1:-1,1:-1] + dt*(a*v[1:-1,1:-1]*(u[1:-1,1:-1]-lam)+ \
...        Dyf_v*(N-1)**2/l**2*(np.diff(v,2,axis=0)[:,1:-1]+np.diff(v,2,axis=1)[1:-1,:]))
...
...       essential_boundary_conditions(u)
...
sage: print "Saved ",len(Tlst), " from ", Nsteps

dt,dt_dyn 0.0201654966800612 0.0200000000000000

sps= 50 dt= 0.0200000000000000 Nsteps= 10000

Saved 200 from 10000

CPU time: 24.83 s, Wall time: 24.82 s

\[\frac{\partial U }{\partial t} = U (1 - U - V)+ \Delta U\]

\[\frac{\partial V }{\partial t} = \alpha V ( U - \lambda) + \Delta V\]

sage: import pylab
sage: @interact
sage: def _(ti=slider(range(len(Tlst)))):
...       print r"t=",dt*ti
...       pu =  matrix_plot(Tlst[ti],origin='lower',cmap='rainbow', figsize=(4,4) )
...       pv =  matrix_plot(Tvlst[ti],origin='lower',cmap='rainbow',figsize=(4,4) )
...       html.table([[pu,pv]])

sage: anim = animate([matrix_plot(u,origin='lower',cmap='rainbow',figsize=(4,4) ,vmin=0,vmax=.01) for u in Tvlst[::10]])

sage: anim.show()

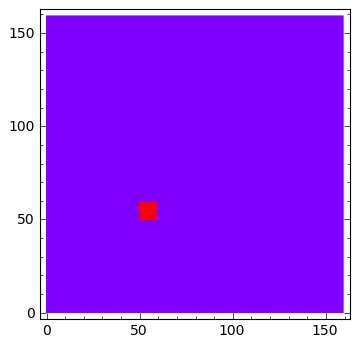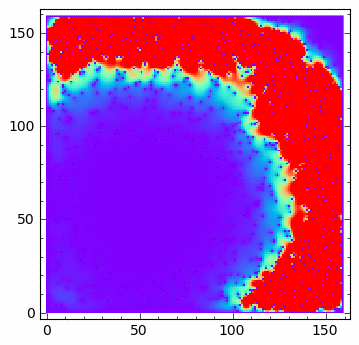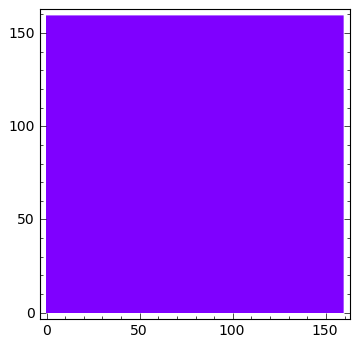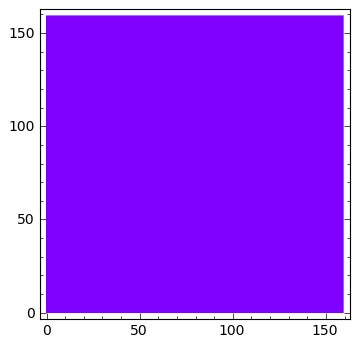
sage: anim.show()

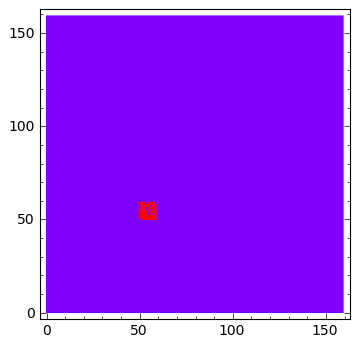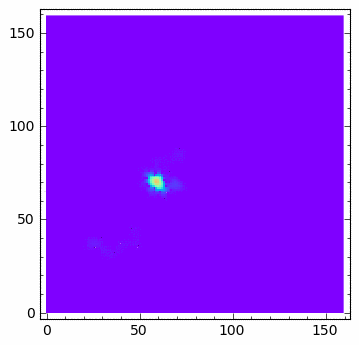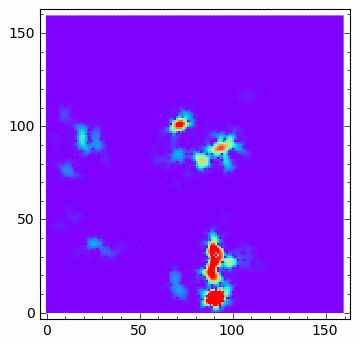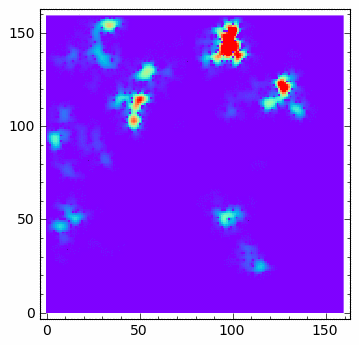
sage: u[np.random.randint(0,u.shape[0],100),np.random.randint(0,u.shape[0],100)] = 1

sage: matrix_plot(u,origin='lower',cmap='rainbow',figsize=(4,4) )

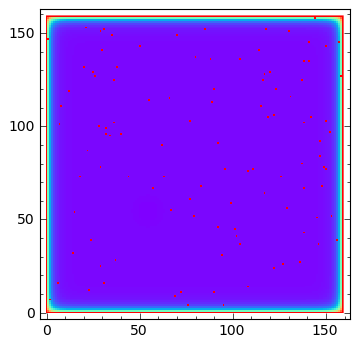
sage: (u-np.roll(u,1,axis=0))*m+(u-np.roll(u,-1,axis=0))*m+(u-np.roll(u,1,axis=1))*m+(u-np.roll(u,-1,axis=1))*m

Model rozprzestrzenienia się epidemii w losowej geometrii

sage: %timeit
sage: import numpy as np
sage: sparse = True
sage: slicing = True
sage: Dyf_u = .0
sage: Dyf_v = 1.02
sage: Dyf = max(Dyf_u,Dyf_v)
sage: a = 1.0
sage: lam = .3
sage: l = 100.0 # dlugosc ukladu
sage: t_end = 50 # czas symulacji
sage: N = 100 # dyskretyzacja przestrzeni
sage: h = l/(N-1)
sage: dt = 0.052/(Dyf*(N-1)**2/l**2) # 0.2 z warunku CFL, krok nie moze byc wiekszy
sage: dt_dyn = 0.02
sage: print "dt,dt_dyn",dt,dt_dyn
sage: dt = min(dt,dt_dyn)
sage: sps = int(1/dt) # liczba krokow na jednostke czasu
sage: Nsteps=sps*t_end  # calkowita liczba krotkow
sage: print "sps=",sps,"dt=",dt,'Nsteps=',Nsteps
sage: # warunek poczatkowy
sage: u = np.zeros((N,N))
sage: v = np.zeros((N,N))
sage: u[:,:]=1.0
sage: v[30:60:,30:60]=0.1
sage: perc =5500
sage: irand,jrand = np.random.randint(0,u.shape[0],perc),np.random.randint(0,u.shape[0],perc)
sage: # maska
sage: m = np.ones((N,N),dtype=np.bool)
sage: if True:
...       m[0,:]=False
...       m[N-1,:]=False
...       m[:,0]=False
...       m[:,N-1]=False
...
sage: m[irand,jrand]=False
...
sage: Lap =lambda u: -((u-np.roll(u,1,axis=0))*np.roll(m,1,axis=0)+(u-np.roll(u,-1,axis=0))*np.roll(m,-1,axis=0)+(u-np.roll(u,1,axis=1))*np.roll(m,1,axis=1)+(u-np.roll(u,-1,axis=1))*np.roll(m,-1,axis=1))
sage: def essential_boundary_conditions(u):
sage: #    global irand,jrand
sage: #    u[irand,jrand]=0
sage: #    v[irand,jrand]=0
...       u[:,0] = 1.0
...       u[:,-1] = 1.0
...       u[-1,:] = 1.0
...       u[0,:] = 1.0
...       v[:,0] = 0.0
...       v[:,-1] = 0.0
...       v[-1,:] = 0.0
...       v[0,:] = 0.0
...
sage: Tlst=[]
sage: Tvlst=[]
sage: essential_boundary_conditions(u)
sage: for i in range(Nsteps):
...       if not i%sps:
...           Tlst.append(u.copy())
...           Tvlst.append(v.copy())
...
...       u[1:-1,1:-1] = u[1:-1,1:-1] + dt*(u[1:-1,1:-1]*( 0.0 - 0*u[1:-1,1:-1]-v[1:-1,1:-1] ) + \
...        Dyf_u*(N-1)**2/l**2*Lap(u)[1:-1,1:-1])
...       v[1:-1,1:-1] = v[1:-1,1:-1] + dt*(a*v[1:-1,1:-1]*(u[1:-1,1:-1]-lam)+ \
...        Dyf_v*(N-1)**2/l**2*Lap(v)[1:-1,1:-1])
...
sage: wall = np.ones_like(u)
sage: wall[np.logical_not(m)]=np.nan
sage: print "Saved ",len(Tlst), " from ", Nsteps
sage: html.table([["U","V"],[matrix_plot(u*wall,origin='lower',cmap='rainbow',figsize=8 ),matrix_plot(v*wall,origin='lower',cmap='rainbow',figsize=8 )]])

dt,dt_dyn 0.0520155006191845 0.0200000000000000

sps= 50 dt= 0.0200000000000000 Nsteps= 2500

Saved 50 from 2500

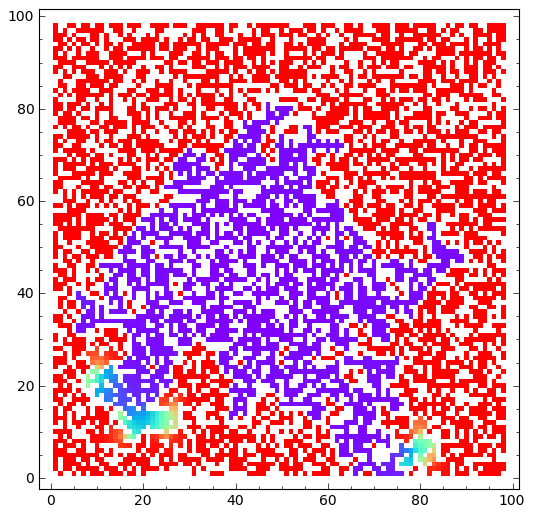
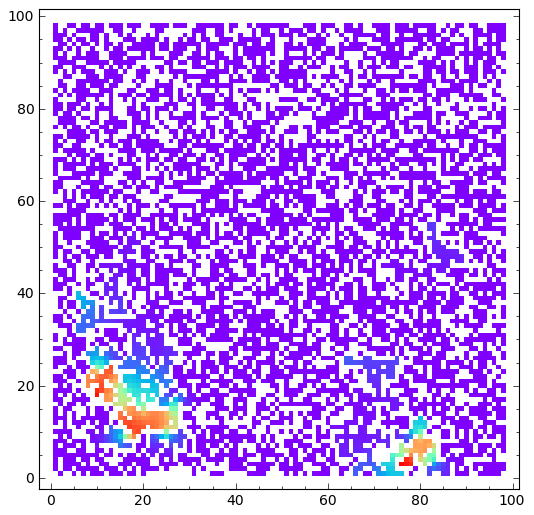
CPU time: 8.68 s, Wall time: 8.68 s

sage: import pylab
sage: @interact
sage: def _(ti=slider(range(len(Tlst)))):
...       print r"t=",dt*ti
...       pu =  matrix_plot(Tlst[ti]*wall,origin='lower',cmap='rainbow', figsize=(4,4) )
...       pv =  matrix_plot(Tvlst[ti]*wall,origin='lower',cmap='rainbow',figsize=(4,4) )
...       html.table([[pu,pv]])

sage: wall = np.ones_like(u)
sage: wall[np.logical_not(m)]=np.nan
sage: anim = animate([matrix_plot(u*wall,origin='lower',cmap='rainbow',figsize=(4,4) ,vmin=0,vmax=1.01) for u in Tlst[::1]])
sage: anim.show()

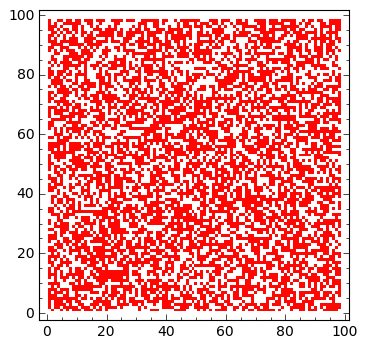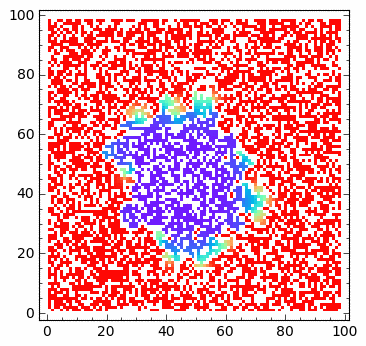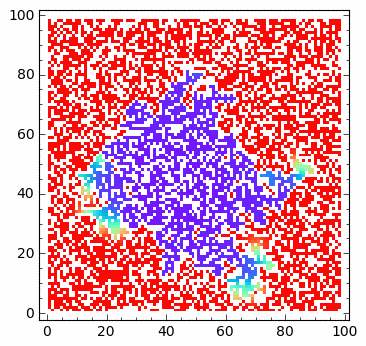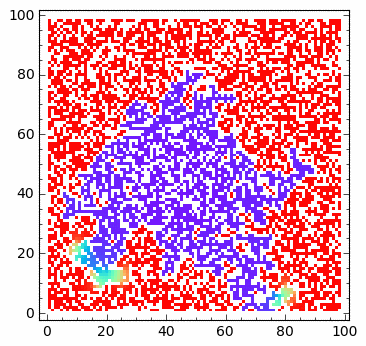
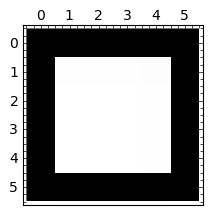
Operator Laplace’a z odbijającą scianką: implementacja z maska.

sage: import numpy as np
sage: N=6
sage: m = np.ones((N,N),dtype=np.bool)
sage: m[0,:]=False
sage: m[N-1,:]=False
sage: m[:,0]=False
sage: m[:,N-1]=False
sage: show(m)
sage: matrix_plot(m,figsize=3)

\[\begin{split}\begin{array}{l} \verb|[[False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False]|\\ \phantom{x}\verb|[False|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{x}\verb|False]|\\ \phantom{x}\verb|[False|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{x}\verb|False]|\\ \phantom{x}\verb|[False|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{x}\verb|False]|\\ \phantom{x}\verb|[False|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{xx}\verb|True|\phantom{x}\verb|False]|\\ \phantom{x}\verb|[False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False|\phantom{x}\verb|False]]| \end{array}\end{split}\]

sage: u=np.random.randn(N,N)
sage: Lap =lambda u: -((u-np.roll(u,1,axis=0))*np.roll(m,1,axis=0)+(u-np.roll(u,-1,axis=0))*np.roll(m,-1,axis=0)+(u-np.roll(u,1,axis=1))*np.roll(m,1,axis=1)+(u-np.roll(u,-1,axis=1))*np.roll(m,-1,axis=1))

sage: show(np.diff(u,2,axis=0)[:,1:-1]+np.diff(u,2,axis=1)[1:-1,:])

\[\begin{split}\begin{array}{l} \verb|[[-3.13448456|\phantom{xx}\verb|5.18465268|\phantom{xx}\verb|2.24718743|\phantom{xx}\verb|1.5615061|\phantom{x}\verb|]|\\ \phantom{x}\verb|[|\phantom{x}\verb|6.81131198|\phantom{x}\verb|-5.12027386|\phantom{xx}\verb|0.45648868|\phantom{x}\verb|-8.70124209]|\\ \phantom{x}\verb|[|\phantom{x}\verb|0.83522291|\phantom{x}\verb|-2.22075512|\phantom{xx}\verb|4.82439459|\phantom{xx}\verb|5.04618174]|\\ \phantom{x}\verb|[|\phantom{x}\verb|4.44827112|\phantom{x}\verb|-5.28018261|\phantom{x}\verb|-5.41145643|\phantom{x}\verb|-2.22106382]]| \end{array}\end{split}\]

sage: show(Lap(u))

\[\begin{split}\begin{array}{l} \verb|[[-0.|\phantom{xxxxxxxxxx}\verb|0.42601275|\phantom{x}\verb|-2.51302703|\phantom{x}\verb|-1.25894388|\phantom{xx}\verb|1.13807986|\phantom{x}\verb|-0.|\phantom{xxxxxxxx}\verb|]|\\ \phantom{x}\verb|[|\phantom{x}\verb|0.34635619|\phantom{x}\verb|-2.36211561|\phantom{xx}\verb|2.67162565|\phantom{xx}\verb|0.98824355|\phantom{xx}\verb|1.49902703|\phantom{x}\verb|-1.20055893]|\\ \phantom{x}\verb|[-1.58676378|\phantom{xx}\verb|5.22454821|\phantom{x}\verb|-5.12027386|\phantom{xx}\verb|0.45648868|\phantom{x}\verb|-6.25692915|\phantom{xx}\verb|2.44431293]|\\ \phantom{x}\verb|[-0.21974371|\phantom{xx}\verb|0.61547921|\phantom{x}\verb|-2.22075512|\phantom{xx}\verb|4.82439459|\phantom{xx}\verb|3.49525843|\phantom{x}\verb|-1.55092331]|\\ \phantom{x}\verb|[-1.49169634|\phantom{xx}\verb|2.81477871|\phantom{x}\verb|-3.81338909|\phantom{x}\verb|-1.7187601|\phantom{xx}\verb|-1.09762113|\phantom{xx}\verb|1.90581171]|\\ \phantom{x}\verb|[-0.|\phantom{xxxxxxxxx}\verb|-0.14179607|\phantom{xx}\verb|1.46679352|\phantom{xx}\verb|3.69269634|\phantom{x}\verb|-0.78236901|\phantom{x}\verb|-0.|\phantom{xxxxxxxx}\verb|]]| \end{array}\end{split}\]