14. Hedging¶
14.1. Hedging: cel operacji zabezpieczenia przed ryzykiem¶
Każda działalność człowieka posiada bardziej widoczny czy też bardziej ukryty element finansowy. Z finansami wiąże się istnienie ryzyka finansowego czyli takiej sytuacji, w której wynik finansowy zaczyna odbiegać od planowanego z powodów zmian sytuacji na rynkach finansowych. Każdy, kto starannie prowadzi działalność gospodarczą chce by ta rozbieżność nie niszczyła szans lepszej i planowanej przyszłości i stara się zapobiegać negatywnym skutkom tych zmian. Ruchy cen na rynkach finansowych wpływają zarówno na aktywa jaki pasywa bilansu firm.
Zabezpieczanie się przed negatywnymi zmianami na rynkach finansowych dotyczących zmienności cen i kursów nosi nazwę hedging’u.
Przykład
Firma kupiła w roku 2005 akcje firmy holenderskiej po 200EUR płacąc 3.25 PLN za EUR, sprzedała je w roku 2013 po 250 EUR, gdy kurs wymiany wynosił 4.20 PLN/EUR. Zwrot z inwestycji wyniósł 40% licząc w Euro lub ok. 62% licząc w PLN. Jaki jest „prawdziwy„ zwrot z inwestycji??? Czy w ogóle coś takiego jak „prawdziwy” w ogóle istnieje? Jak często należy określać rentowność?? Codziennie???
Ten przykład ilustruje problemy z ryzykiem firmy w aspekcie księgowym.
Cena posiadanego aktywa wzrosła, co zapewnie cieszy właściciela, ale gdyby zmalała, to dał by się odczuć aspekt strat w transakcjach bieżących.
Inny aspektem jest aspekt ryzyka zmian w dłuższym terminie. Posiadacz długiej pozycji w instrumentach rynku kapitałowego będzie się obawiał o to, że ich cena może spaść w pewnym okresie czasu. Przykładowa posiadana w portfelu akcja firmy holenderskiej kupiona po 200EUR, ostatnio była wyceniona na 230 EUR, czy akurat cena jej wzrosła. A co by było gdyby zmalala?
Nic dziwnego, ze będzie się starał o zabezpieczenie się przed taką ewentualnością.
W zależności od potrzeb, umiejętności i wielkości prowadzonych operacji zabezpieczający używają różnych sposobów zabezpieczania się przed ryzykiem. Stosują różne instrumenty i strategie. Nie istnieje bowiem jeden optymalny, „jedynie właściwy” sposób zabezpieczenia. Zarówno metoda zabezpieczenia, zestaw stosowanych technik i instrumentów zależy od sytuacji i celu zabezpieczającego. Najważniejszym jest bowiem rozumienie jaki cel chce się osiągnąć i jak funkcjonuje rynek i jakie instrumenty mogą być pomocne, biorąc pod uwagę, ich mocne ich strony jak i ich niedostatki. Należy pamiętać, że zabezpieczanie się przed ryzykiem rynkowym kosztuje, ale koszt ten jeśli jest niższy od możliwych strat jest często wartym poniesienia.
Nie podjęcie decyzji o zabezpieczeniu się przed ryzykiem jest naturalnie podjęciem decyzji o jego absorbcji. Z wszystkimi konsekwencjami tej decyzji. Czasami takie działania wynikają nie z braku świadomości ryzyka czy braku umiejętności hedgingu. Często taka metoda stosowana jest przez firmy mające możliwość przełożenia ryzyka na kontrahentów. Przykładem takiej strategii są działania firm dostarczające paliwa na rynek. Jako klienci tych firm, kupując na stacjach benzynowych paliwo odczuwamy na sobie wszelkie zmiany cen ropy jak i zmiany cen waluty.
Tak, niejako, przy okazji, poznajemy na sobie najprostszą z metod postępowania z ryzykiem czyli przesuwania jego efektów na innych.
Jak więc wynika z powyższego opisu celem hedgingu jest przesunięcie ryzyka jednego podmiotu gospodarczego na inny. Instytucja (osoba) która pozbywa się ryzyka nazywana jest zabezpieczającym (hedger). Nie wszystkie instytucje „uciekają” od ryzyka. Na rynku istnieje wiele instytucji i osób specjalizujących się w braniu ryzyka na siebie w zamian za oczekiwane korzyści tej usługi. To ta grupa uczestników rynku daje mu płynność i sprawne funkcjonowanie.
Różne aspekty ryzyka, jego skutki oraz podejmowane działania wynikają z celu jaki sobie stawiamy w stosunku do ryzyka.
Zabezpieczający zabezpiecza się przed niekorzystnym z jego punktu widzenia ruchem cen aktywa, które jest mu potrzebne do funkcjonowania na rynku oraz/ lub wzrostem zmienności ceny, co prowadzi do wzrostu ryzyka zajętej pozycji.
Innymi słowy uczestnik rynku zajmujący pozycje długą (Long) będzie obawiał się spadku cen aktywa (zmiana wartości pozycji w Aktywach) i będzie starał się przed nim zabezpieczyć. Inaczej posiadacz pozycji krótkiej (Short), ten będzie się obawiał wzrostu ceny (wzrost wartości zobowiązań w Pasywach) i będzie się chciał zabezpieczyć przed takim scenariuszem.
W celu zabezpieczenia należy znaleźć taki instrument zabezpieczający, który pozwoli „zdjąć” całe (lub prawie całe) ryzyko z zabezpieczającego. Tzn. znaleźć taki instrument, którego ruch ceny odzwierciedla, jak najlepiej, ruch cen zabezpieczanego aktywa.
Zabezpieczenie idealne to takie zabezpieczenie, w którym ruch cen instrumentu zabezpieczającego jest dokładnie negatywnie skorelowany z ruchem cen aktywa zabezpieczanego.
Niestety, bardzo często nie jest możliwe stworzenie idealnego zabezpieczenia, gdyż dokładnie skorelowany instrument zabezpieczający jest niedostępny, albo inaczej nie istnieje na rynku. W takim przypadku stosuje się tylko częściowe (niepełne) zabezpieczenie. Takie rozwiązanie jest często lepsze niż poniechanie procesu zabezpieczania.
14.2. Ryzyko walutowe i ryzyko zmiany ceny¶
Firmy prowadząc swą działalność poddane są efektom ryzyk ich działalności. Oba wymienione w tytule ryzyka dotyczą firm, których działalność opiera się na korzystaniu z międzynarodowych rynków finansowych. Do tej grupy nalężą firmy kupujące/sprzedające surowce na rynku globalnym.
Krótkie spojrzenie na takie firmy uwidacznia dwie sytuacje. Firma sprzedając swe produkty chce, by cena za jej produkty nie zmalała. Firma, która kupuje za granicą, np. surowiec chce by jego cena nie wzrosła. Takie zachowanie bowiem gwarantuje firmom uzyskanie założonego wyniku finansowego oraz generowanie zysku, co jest głównym powodem ich funkcjonowania.
Jeśli ich działalność dotyczy korzystania z rynków zagranicznych to szczególnie w przypadku polskich firm narażone są na ryzyko walutowe. Złoty w odróżnieniu od euro czy USD, nie jest walutą używaną przez inne niż Polska kraje. Najczęściej aktywa na rynkach światowych wyceniane są w USD.
Nawet jeśli ceny aktywów pozostają niezmienne, na wyniki finansowe firm ma jeszcze wpływ kurs waluty. Firmy w swym dążeniu do maksymalizacji zysków mają przeciwstawne oczekiwania co do zmian kursu waluty. Firmy sprzedające produkt za granice są zainteresowane w tym, aby za każdą jednostkę waluty obcej wpływów dostać jak najwięcej jednostek waluty polskiej, czyli chcą aby waluta polska była słaba. Firmy natomiast kupujące za granicą chcą płacić za każdą jednostkę waluty obcej jak najmniejszą ilość polskich złotych, czyli są zainteresowane w tym by polska waluta była jak najsilniejsza.
Te różne oczekiwania spowodowane są tym, że ich wpływy (aktywa) są denominowane w innej walucie niż koszty (wypływy, pasywa). Ryzyko jakie występuje w tej sytuacji to ryzyko kursowe. O istnieniu ryzyka kursowego boleśnie się przekonali Ci, którzy brali kredyty hipoteczne we CHF a spłacali je w PLN. W momencie silnej aprecjacji CHF ich raty kredytów boleśnie wzrosły.
Jak wspomniane firmy mogą w takiej sytuacji zabezpieczać się przed ryzykiem?
Najprostsza metoda eliminacji takiego ryzyka to doprowadzenie do takiej sytuacji by wpływy były w tej samej walucie co wydatki i to najlepiej w tym samej wielkości. Jest to bardzo naturalna metoda zabezpieczenia i niezwykle skuteczna.
Innym sposobem zabezpieczenia się przed ryzykiem kursowym jest zabezpieczenie dostaw waluty po niezmiennym kursie. Ale takie zabezpieczenie wymaga już używania innych, bardziej złożonych technik i instrumentów finansowych. Przykładem takiego rozwiązania są kontrakty forward omówione w części „Wprowadzenie do Funkcjonowania Rynków finansowych” link. Wadą takich kontraktów jest to, że jako kontrakty OTC, są mało płynne i każde nawet małe opóźnienie czasu wpływów powoduje duże problemy płynnościowe kupującego taki kontrakt.
Analizując sytuacje omawianych firm obserwuje się, że oprócz wspomnianego ryzyka kursowego (PLN nie jest walutą światową jak USD czy EUR) występuję w ich przypadku ryzyko rynku, czyli wahań cen surowców. Surowce te na globalnym rynku wyceniane są zazwyczaj w którejś z głównych walut światowych.
Eksporter czyli producent surowca chcąc rozsądnie zarządzać finansami firmy musi kalkulować cenę surowca, który zamierza sprzedawać w przyszłości tak by móc zapewnić działanie swej firmy. Obawia się, aby ceny produkowanego przez niego surowca, np. miedzi, złota, srebra albo przykładowo produktów rolnych nie spadły poniżej pewnego znanego mu poziomu. Jego naturalna pozycja rynkowa jest LONG i jest zainteresowany by cena dostawy była odpowiednio wysoka. Chętnie będzie negocjował kontrakty długoterminowe na dostawy swej produkcji po cenach, które dzisiaj może zaakceptować i ustalić na przyszłość tak by stabilizować produkcję swej firmy w przyszłości.
Importer surowca, firma kupująca surowiec by przykładowo zrobić z niego inny produkt, jest zainteresowana by kupować go najtaniej i ustalić tanie ceny na przyszłość. Przykładem może być producent kabli elektrycznych, który używa miedzi jako surowca do produkcji. Importer ma naturalną pozycję SHORT i interesują go najniższe możliwe ceny dostaw. Jak widać ich pozycje negocjacyjne są przeciwstawne.
Jeśli cena rynkowa surowca jest akceptowalna, to obie strony są interesowne w zawarciu kontraktów na przyszłość po ustalonej cenie, czyli kontraktów forward. Taki kontrakt pozwala na racjonalne zarządzanie finansowe i stabilizuje sytuacje firmy. Kontrakty forward lub futures są stosowane często w takich przypadkach bo ustalają przyszła cenę.
Niestety cena na rynkach zmienia się i każda ze stron może po upływie pewnego czasu, nie być zadowolona z wynegocjowanej ceny dostaw. Cena rynkowa bowiem może być dużo wyższa (strata producenta) lub dużo niższa (strata importera). Cena nawet w kontraktach na długie terminy dostaw nie jest raczej stała w zbyt długim okresie czasu. Rynek dyktuje jej zmienność.
W takich przypadkach strony długoterminowych umów zgadzają się na stosowanie cen średnich z ustalonych okresów czasu. Najczęściej jednak decydują się na stosowanie cen rynkowych i stosowanie metod zabezpieczenia swych interesów zabezpieczając się przed wahaniami cen rynkowych.
14.3. Zabezpieczenie przy pomocy kontraktów Futures¶
Short hedge, Long hedge.
U podstaw korzystania z rynku terminowego futures leżą następujące fakty:
Ponieważ ceny na rynku futures i rynku spot dotyczą tego samego aktywa (surowca) w dniu dostawy ceny te powinny być równe. Gdyby nawet pojawiła się możliwość arbitrażu między rynkami to czujni uczestnicy rynku z niej skorzystają i ceny szybko się wyrównają.
Jeśli zajmiemy na rynku terminową pozycję odwrotną do pozycji na rynku natychmiastowym, to jeśli ceny będą wzrastać to zysk na jednej pozycji będzie równy stracie na drugiej tak jak pokazuje to rysunek

Zasada hedgingu przy pomocy kontraktów Futures. Cena kupna kontraktu na jednym rynku zachowuje się odwrotnie do ceny sprzedaży na drugin rynku.¶
Innymi słowy w wyniku takiego zabiegu sumaryczny wynik ewentualnych zysków czy strat będzie równy zero czyli wynik finansowy nie ulega zmianie bez względu na wahania ceny.
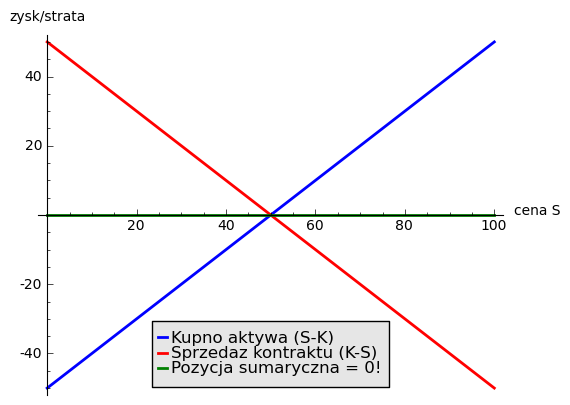
Zabezpieczenie się przed zmianą ceny przy pomocy kontraktu futures.¶
Przykład pokazany na rysunku pokazuje sytuacje zabezpieczenia się przed zmiana spadkiem ceny na posiadane aktywo (surowiec). Obawiając się spadku ceny w przyszłości (strata) producent sprzedaje kontrakt terminowy (futures) na tą sama ilość surowca (i dla uproszczenia przyjmijmy z taką samą datą dostawy jak kontrakt dostawy fizycznej).
W tej sytuacji możliwa strata z powodu możliwego spadku ceny jest wyrównywana przez zysk na transakcji terminowej.
Taka transakcja zabezpieczająca nazywa się Short Hedge, gdzie short opisuje akcje sprzedaży (przyjęcia pozycji short) aktywa (surowca, akcji, itd.) jako instrumenty pochodnego (futures) co zabezpiecza przed stratami spadku ceny instrumentu posiadanego. Zastosowanie właściwe takiej strategii pozwala na to by zyski z instrumentu pochodnego równoważyły straty z pozycji długiej (i odwrotnie).
Short hedge jest często stosowana strategia zabezpieczania przez producentów (surowce, produkty spożywcze, etc.), którzy chętnie poniosą pewne koszty „zamrażając” ceny w przyszłości.
Dla zobrazowania powyższego postepowania można sobie wyobrazić producenta surowca przykładowo; producent miedzi ( podobnie postepować będzie gospodarstwo rolne, itd.), który musi w przyszłości dostarczyć wytwór swej pracy po cenie rynkowej i obawia by cena ta nie była niższa niż koszty wytwarzania produktu.
Przykład
Cena miedzi utrzymuje się na rynku kasowym wynosi 3.21 USD za funt (ok. 0.5kg) a wielkość kontraktu wynosi 25 000 funtów (notowania COMEX). Producent wie, że powinien dostarczyć za dwa miesiące 25 000 funtów miedzi na rynek. Dla uproszczenia wielkość dostawy to wielkość 1 kontraktu giełdowego na dostawę miedzi w przyszłości. Obawia się by cena rynkowa w chwili dostawy nie była niższa niż jego koszty wytwarzania, które wynoszą (powiedzmy) 2.89 USD za funt, czyli 72 250 za kontrakt. Dzisiejsza cena miedzi na rynku terminowym futures wynosi 3.18 USD za funt na miedz w terminie dostawy za dwa miesiące. Chcąc się zabezpieczyć producent sprzedaje kontakt futures na dostawę za dwa miesiące za cenę 3.18 USD za funt czyli 79 500 USD za kontrakt.
Za dwa miesiące cena miedzi na rynku kasowym (i na dostawę w tym samym czasie na rynku futures) wynosi 2.8 USD za funt czyli 70 000 USD za kontrakt. Czyli zysk jaki odnotował ze sprzedaży futures wyniósł 79 500 - 70 000 = 9 500 USD Sprzedając miedź na rynku kasowym odnotował wynik:
wpływ ze sprzedaż: 70 000 USD
koszty wytworzenia: 72 250 USD,
czyli stracił 70 000 - 72 250 = - 2 250 USD. Uwzględniając zyski z rynku futures całkowity jego bilans jest dodatni:
9 500 - 2 250 = 7 250 USD
Innymi słowy mimo, że rynek zmusił producenta do sprzedaży poniżej kosztów wytworzenia jego wynik finansowy jest dodatni, czyli odnotowuje zysk mimo spadku ceny.
Zabezpieczenie zadziałało.
Podobną strategię zastosuje firma, która pożyczyła 10 milionów w banku na 1% powyżej trzymiesięcznej stopy depozytowej z prawem rolowania co kwartał. W dacie następnego rolowania stopa procentowa może być wyższa, więc firma decyduje się zabezpieczyć poprzez sprzedaż trzy miesięcznych kontraktów futures na stope procentową o wartości nominalnej odpowiadającej pożyczce bankowej. Niech trzymiesięczna stopa depozytowa (referencyjna) wynosi 12% rocznie.
Sytuacja na początku transakcji:
Rynek natychmiastowy (kasowy) |
Rynek futures |
|---|---|
Maj |
|
Pożyczyła po 13% + (12% +1%) |
Sprzedała kontrakty marcowe na trzymiesięczną stopę po cenie, załóżmy, 87,75 (100-12,25%) |
Czerwiec |
|
Firma roluje, czyli pożycza znów 10 milionów na trzy kolejne miesiące po 14% (13%+1%) |
Skupuje z rynku kontrakty je zgodnie z 86,75 tj.( 100-13,25%) |
Czyli płaci dodatkowe odsetki za jeden kwartał czyli 10 000 000(0.14-0.13)/4 = 25 000 |
|
Czyli doskonałe zabezpieczenie bo zysk z rynku futures pozwala na utrzymaniu kosztu kredytu na poziomie niezmiennym 13% rocznie mimo zmiany stopy oprocentowania.
W przypadku importera, czyli uczestnika rynku, który naturalnie potrzebuje kupować aktywa (surowce) na rynku wykorzystanie rynku instrumentów pochodnych do zabezpieczania jest podobne chociaż pozycje zajmowane są odwrotne w stosunku do sytuacji powyżej.
Long Hedge jest to strategia stosowana by zachować w przyszłości dzisiejszą cenę dostawy. Czyli firma wie, że w przyszłości musi kupić aktywo (surowiec) i chce „zamrozić” jego cenę zakupu.
Inwestor zajmuje pozycje długą na rynku terminowym w celu zabezpieczenia się przed zmiennością przyszłej ceny.
Long hedge jest stosowany również by zabezpieczyć krótka pozycje zajętą na rynku przez inwestora.
Jako przykład niech posłuży ta sama, co w poprzednim przykładzie, firma. Tym razem, oczekuje za dwa miesiące wpływu 2 milionów. Pieniądze te zamierza firma ta ulokować na depozycie krótkoterminowym. Firma (a właściwie jej zarząd) obawia się, że stopy depozytowe spadną zanim pieniądze wpłyną do firmy i zamierza się przed skutkiem takiej zmiany zabezpieczyć, kupując znane z poprzedniego przykładu kontrakty terminowe na stopę trzymiesięczną. Oczywiście, ich liczba wynika z wartości kwoty zabezpieczanej. Jest to strategia Long Hedge
Czyli
Czas |
rynek natychmiastowy(kasowy) |
Rynek terminowy (futures) |
luty |
stopa depozytowa 11% |
zakup majowych kontraktów terminowych na trzymiesięczną stopę za 88.5%=100%-11,5% |
maj |
inwestuje 2mln na 9.%, |
sprzedaje kontrakty po 90.5%=100%-9.5% |
zysk/strata |
|
\(\times\) 10 000 zysk=10 000 |
Czyli mimo spadku stopy depozytowej zysk z transakcji na instrumentach pochodnych pozwolił na utrzymanie wyniku finansowego na niezmienionym a korzystnym dla firmy poziomie.
Czyli jawi się jasna zasada:
Zasada I
Jeśli mamy pozycje krótką na rynku natychmiastowym (kasowym). Innymi słowy, oczekujemy wpływu płatności i obawiamy się wzrostu cen lub spadku stóp procentowych, to kupujemy futures (stosujemy long hedge).
Zasada II
Jeśli mamy pozycje długą na rynku natychmiastowym (kasowym). Innymi słowy trzymamy gotówkę lub aktywo i martwimy się, że ceny spadną albo stopy wzrosną to sprzedajemy futures. Czyli stosujemy short hedge.
Dotąd zakładaliśmy, że zabezpieczona jest cała kwota wynikająca ze strategii i że dzień dostawy na rynku terminowym przypada w dniu transakcji na rynku kasowym. Teraz powoli uwolnimy się od uproszczeń. Popatrzmy formalnie na stosowane strategie.
W strategii short hedge mamy następującą formalną sytuację. Niech \(F_1\) oznacza cenę początkową kontraktu futures, a \(F_2\) cenę końcową futures, \(S_2\) końcową cenę aktywa kasowego. To wejściu w strategie short hedge cena realizacji strategii będzie równa:
W przypadku wejścia w pozycje długą, celem zabezpieczenia (long hedge) koszt aktywa wynosi:
Ten rodzaj strategii zawiera w sobie pewne ryzyko niedopasowania rynku terminowego do rynku kasowego. Różnica między ceną kasową a rynku terminowego to tzw. baza albo basis. O tym było mówione przy omawianiu rynku i kontraktów terminowych (patrz: Opcje). Warto pamiętać o bazie jak i o cost of carry.
Ryzyko bazy, a właściwie jego skutki czasem powoduje bardzo duże zaskoczenie tak, jak to miało miejsce w transakcjach Metallgeselschaft AG. Firma ta doświadczyła boleśnie istnienia ryzyka bazy w handlu nie metalami (jak by to mogło kojarzyć się z nazwą), ale ropa naftową, przy rolowaniu zabezpieczenia.
Powstaje pytanie ile kontraktów futures jest potrzebne do zabezpieczenia pozycji kasowej?
W celu odpowiedzi konstruujemy portfel z długiej pozycji kasowej i krótkiej pozycji \(\boldsymbol{h}\) jednostek odpowiednich kontraktów futures. Wartość \(\boldsymbol{W}\) portfela to:
gdzie:
\(\boldsymbol{P_k}\) - wartość pozycji kasowej,
\(\boldsymbol{P_f}\) wartość kontraktu futures,
\(\boldsymbol{h}\) - współczynnik zabezpieczenia.
Optymalna wartość \(h\) to taka wartość, gdy zabezpieczenie będzie idealne, czyli zmiana wartości portfela nie ulegnie zmianie niezależnie czy wartość kasowego aktywa wzrośnie czy zmaleje.
Czyli:
Stąd:
Czyli ilość kontraktów futures \(I_f\) potrzebna do zabezpieczenia pozycji na rynku kasowym jest równa:
W przypadku dyskutowanych przykładów powyżej zmiany ceny aktywa na rynku futures były takie same jak zmiany ceny aktywa na rynku kasowym. Niestety nie zawsze tak jest w praktyce i co za tym idzie, idealne zabezpieczenie nie zawsze jest możliwe.
A to dlatego, że:
Zabezpieczane aktywo może nie być dokładnie takie samo jak aktywo będące podstawą kontraktu futures. Przykładowo dla rynku surowców może różnic się co do wagi, jakości, ilości jak i samego surowca (szukanie aktywa o podobnym zachowaniu) .
Zabezpieczając możemy nie znać dokładnego terminu zakupu lub sprzedaży aktywa.
Kontrakt futures może wymagać zamknięcia go przed jego miesiącem dostawy
Wtedy jesteśmy zmuszeni zadowolić się częściowym zabezpieczeniem. Nie zawsze istnieje kontrakt pochodny oparty na tym samym aktywie i musimy dopasować instrument zbliżony do kasowego, którego zmiany nie dokładnie korelują ze zmianami instrumentu podstawowego. Takie zabezpieczenie nazywane jest cross hegde w odróżnieniu od direct hedge, czyli sytuacji z poprzednich przykładów gdy korelacje zmian były pełne.
14.3.1. Cross hedging¶
Ponownie rozważmy definicje bazy - basis. Baza (basis) to różnica między ceną kasową aktywa zabezpieczanego a ceną kontraktu futures na to aktywo. Jeśli zabezpieczane aktywo jest identyczne co aktywo podstawowe dla kontraktu futures, cena aktywa na rynku kasowym i cena kontraktu futures powinny „zbiegać się” (konwergencja) w pobliżu terminu dostawy futures. Ta konwergencja nazywana jest też ceną bazy.
Zachowanie bazy generalne cechuje: a. Sezonowość zachowania b. Zmienność bazy jest zazwyczaj mniejsza niż zmienność ceny c. Cena bazy wprowadzić może dodatkowe ryzyko zmiany ceny powyżej, jak i poniżej ceny futures. To zachowanie zaburza perfekcyjność zabezpieczenia. Ponadto, jeśli okresy do do dostawy użytych instrumentów będą różne to zabezpieczenie nie będzie już tak idealne jak w przypadku gdy termin dostawy instrumentu kasowego i dostawy instrumentu futures będą równe. Współczynnik h nie jest wtedy równy 1. W takich przypadkach stosuje się zabezpieczenie „cross hedge”.
Praktyczna wskazówka przy stosowaniu tego typu hedgingu jest nastepująca: w przypadku gdy terminy dostawy dostępnych kontraktów na rynku futures nie zgadzają się z terminami zabezpieczenia to wybierając kontrakt futures kierować się należy tym, by data dostawy (miesiąc) był najbliższy terminowi transakcji na rynku kasowym ale późniejszy niż czas zabezpieczenia. Jeśli nie ma kontraktu futures na aktywo zabezpieczane należy wybierać kontrakt futures, którego cena jest najlepiej skorelowana z ceną zabezpieczanego aktywa. Korelacje taką określa się poszukując najmniejszej wariancji.
14.3.2. Zabezpieczenia metodą najmniejszej wariancji¶
Jeśli czasy dostawy użytych instrumentów będą różne to należy pamiętać o cost of carry. Szczególnie instrumenty dłużne mają skomplikowaną zależność generowanego dochodu od duration i stopy procentowej.
Tak więc reakcja instrumentu kasowego i terminowego mogą być różne, tzn. ich zmiany mogą być inne na koniec okresu zabezpieczenia.
Jasnym jest, że zmiany aktywów na rynku kasowym i terminowym nie są takie same (chociaż w jakimś stopniu podobne). Jak to wpłynie na współczynnik h? Jak wybrać najlepsze h?
Można w takiej sytuacji skorzystać z takiego h które minimalizuje następujące równanie:
Czyli minimalizujemy kwadraty różnic między zmianami cen.
Innymi słowy takie h to hedging minimalizujący wariancje - hedging minimalnej wariancji.
Popatrzmy jeszcze raz na \(\boldsymbol{\Delta W}\) - zmianę wartości portfela zabezpieczonego:
gdzie:
Zabezpieczenie jest optymalne jeśli powyższa pochodna cząstkowa wariancji zmian portfela po współczynniku hedgingu się zeruje, czyli:
stąd:
- czyli biorąc pod uwagę, że współczynnik korelacji \(\Delta P_k\) i
\(\Delta P_f\) - \(\rho\) jest równy z definicji:
otrzymujemy ostatecznie znany wzór:
Można także oszacować optymalny współczynnik zabezpieczenia h używając analizy regresji.
Podstawowe równanie wyjściowe ma w tym przypadku następująca postać.
Używając regresji liniowej (najmniejszych kwadratów) wyliczymy, że
Metoda powyższa jest pomocna w wielu przypadkach. Poniże rozpatrzone będą pewne przykłady zastosowania tej metody, przedstawione by lepiej zilustrować sposoby postępowania w takich przypadkach.
Zarządzający portfelem, mający portfel instrumentów inwestycyjnych o określonej jego wartości w danym dniu może chcieć zabezpieczyć jego wartość w najbliższym okresie czasu. Spodziewa się bowiem przykładowo, że cena aktywów może chwilowo się obniżyć ale uważa, że posiadane w portfelu aktywa są warte trzymania.
Informacja
Alternatywnym działaniem może być sprzedanie całego portfela, by odkupić go później, po powrocie rynku do oczekiwanych wartości. Takie działanie jest możliwe teoretycznie ale bardzo trudne w praktyce do wykonania z powodu dostępności aktywów i kosztów transakcyjnych opisanych operacji.
Chcąc zabezpieczyć posiadany portfel na rynku instrumentów futures jest niezwykle trudno, wręcz niemożliwym jest, by znaleźć kontrakt futures odpowiadający swym zachowaniem zachowaniu czasowemu portfela. Sposób w jaki można próbować się zabezpieczyć przed zmianami stanu posiadania jest zabezpieczenie przy pomocy kontraktu futures na indeks giełdowy. Przykład poniżej ilustruje sposób postępowania i szukania współczynnika korelacji zmian wartości portfela i kontraktu futures na indeks, potrzebnego do najlepszego w miarę możliwości ( nie idealnego) zabezpieczenia portfela.
Jak używać kontraktów futures do zabezpieczania portfela?
Załóżmy ,ze posiadamy portfel zdywersyfikowanych akcji. Powiedzmy, ze o wartości 1 miliona USD ( waluta i skład portfela wybrany do wyjaśnienia przykładu poniżej- czyli użycia kontraktu futures na indeks S&P 500- podobnie można myśleć używając innych indeksów rynkowych na które są kontrakty futures)). Wybieramy kontrakt futures na indeks S&P 500 celem zabezpieczenia portfela. Obawiamy się, że rynkowa wartość portfela może się obniżyć. W takiej sytuacji sprzedaż kontraktu futures na indeks może być sposobem na zabezpieczenie się przed obniżeniem się wartości portfela.
Jeśli rynek spadnie zysk na pozycji krótkiej na rynku futures może zrównoważy stratę na portfelu. Jeśli rynek jednak wzrośnie stratę na pozycji futures będzie pokrywać zysk na portfelu.
Kontrakt futures na indeks S&P 500 jest wyceniany jako wartość indeksu pomnożoną razy 250 USD. Czyli zakładając, że wartość indeksu wynosi 2000 jego wartość kasowa wynosi 500 000 USD. Czyli dwa kontrakty Futures stanowią wartość porównywalną z wartością kasową portfela.
Kontrakty futures na indeks S&P 500 mają cztery daty dostawy w roku. Marcową, czerwcowa, wrześniową i grudniową. Na rynku są dostępne również kontrakty e – mini S&P 500 których wartość jest 50 USD razy wartość indeksu.Te często dają lepsze dopasowanie do wielkości portfela dzięki mniejszemu mnożnikowi niż typowe kontrakty na indeks S&P 500.
Pierwszym krokiem do zabezpieczenia jest znalezienie korelacji zmian indeksu i zmian wartości portfela. Stad można wyliczyć ilość kontraktów które należy sprzedać by zabezpieczyć portfel.
Przykład zamieszony poniżej ilustruje sposób działania.
14.3.3. Zabezpieczenie portfela indeksem giełdowym¶
Załóżmy, że mamy portfel o wartośći rynkowej i chcemy zabezpieczyć tę wartość przed zmianami kursu za pomocą indeksu giełdowego. W kolejnych kolumnach znajdują się wartości portfela oraz indeks S&P500 z okresu 2000-09-15 do 2002-09-19. Używamy tych danych do zabezpieczenia kontraktem Futures na S&P500 w ostatnim dniu - czyli 2002-09-19.
Ponieważ zarówno indeks jak i wartość portfela jest w „innych jednostkach”, możemy posługiwać się bezwymiarowymi zwrotami, zamiast przyrostów cen. I tak zwroty z portfela i S&P500 obliczamy:
Z tych danych widzimy, że zachodzi duża korelacja między zwrotami portfela i indeksu. Współczynnik dopasowania obliczamy ze wzoru:
Zauważmy, że mając obliczone „hedge ratio” - \(h\), liczbę kontraktów wyliczamy mnożąc \(h\) przez ilość jednostek S&P500, które w chwili zabezpieczenia mają dokładnie wartość naszego portfela. Oczywiście nie można kupować ułamkowej ilości kontraktów futures. Zabezpieczający się musi kupić 5 kontraktów.
Dopasowując model linowej zależności zwrotów otrzymamy znowu ten sam wynik:
14.4. Przykład obliczeń hedgingu za pomocą kontraktów futures¶
Metoda najmniejszej wariancji jest skutecznie stosowana w procesie zabezpieczania się przed zmiennością ceny paliwa lotniczego stosowaną przez niektóre linie lotnicze. Tak się składa, że kontrakty futures na paliwo lotnicze są rzadkością na rynku i do zabezpieczania stosuje się kontrakty futures na olej opałowy, które to kontrakty są bardziej płynne. Porównując ceny paliwa lotniczego i ceny oleju opałowego widać, że zmienność ceny obu surowców jest w pewnej mierze podobna ale nie identyczna. Problemowi zabezpieczania cen paliwa lotniczego przy pomocy instrumentów rynków futures poświęcone są poniższe pozycje:
Problem ten jest szeroko dyskutowany i analizowany literaturze fachowej.
14.4.1. Paliwo lotnicze oraz olej opałowy¶
Rozważmy następujący przykład. Chcemy zabezpieczyć cenę na paliwo lotnicze na jeden miesiąc do przodu mając do dyspozycji kontrakty Futures na olej opałowy na 60 i 90 dni. Oczekuje się, że istnieje duża korelacja pomiędzy tymi surowcami. Rzeczywiście, ich historyczne comiesięczne notowania wyglądają następującą:
Informacja
W pliku z danymi mamy w wierszach comiesięczne notowania, a w kolumnach kolejno: cenę paliwa lotniczego, cenę kontraktu Futures na 90 dni i na 60 dni.
Korelację widać gołym okiem, ale oczywiście możemy ją obliczyć numerycznie korzystając z narzędzi znajdujących się w bibliotece numpy. Uczynimy to w dwóch krokach. W pierwszej kolejności obliczmy miesięczne zmiany cen. Dla wartości ceny paliwa lotniczego na rynku kasowym jest to proste: obliczamy różnicę pomiędzy każdą parą kolejnych wartości. Dla kontraktu Futures jest trochę bardziej skomplikowane zadanie. Jeżeli kupimy kontrakt 90 dniowy to po 30 dniach mamy kontrakt 60 dniowy w ręce. Dlatego, mając możliwość handlu kontraktami 60 i 90 dniowymi możemy efektywnie użyć ich do hedgingu na 30 dni, biorąc różnicę między ceną kontrakty 60 dniowego a ceną 90 dniowego po miesiącu.
Informacja
Gdybyśmy mieli do dyspozycji kontrakty 30-dniowe na olej opałowy obliczylibysmy po prostu różnice ich kolejnych cen.
W Sage obliczenia możemy wykonać w następujący sposób:
Możemy teraz policzyć macierz kowariancii przyrostów cen oraz ich współczynnik kolelacji:
Jaki będzie współczynnik zabezpieczenia? Gdyby udało nam się uzyskać idealy hedging to zachodziło by:
Jest to pewnie nie możliwe, ale przynajmniej chcemy znaleźć takie \(h\), które minimalizuje \(\langle\Delta S - h \Delta F \rangle^2\). Narysujmy wykres tej średniej po naszych danych historycznych:
Taki sam wynik otrzymamy dopasowując dane przyrostów cen do siebie w modelu liniowych (co jest czasem zwane regresją liniową):
Przypadek zabezpieczania w przypadku instrumentów opartych o stopę procentową
Jako ilustracje powyższych rozważań przykładowo zadajmy sobie pytanie: Ile kontraktów terminowych na stopę procentową potrzebujemy by zabezpieczyć 10 000 000 (np. BPF) instrumentu pieniężnego. Jeśli to funty to wielkość nominalna kontraktu futures - 500 000. Jak widać do zabezpieczenia kredytu z ostatniego przykładu potrzebowaliśmy 20 kontraktów. Ile trzymiesięcznych kontraktów futures na stope procentową potrzebujemy do zabezpieczenia 10 000 000 BPF w półrocznych CD.
Instrumenty te różnią się czułością na stopę procentową.
Biorąc pod uwagę powyższe, ilość kontraktów futures \(I_f\) potrzebna do zabezpieczenia wynosi
\(I_f =\frac{\text{ Wart. nom. pozycji kasowej}}{\text{Wart. nom. kontraktu futures}}\times \text{wsp. odpowiedniości pieniężnej}\times\text{wsp regresji}.\)
Czyli h jest równe iloczynowi dwu wielkości: współczynnikowi odpowiedniości pieniężnej K i współczynnikowi regresji R.
Wartość odpowiedniości pieniężnej T mierzy zmianę ceny kontraktu terminowego lub aktywa kasowego w zależności od stopy procentowej. Zależy ta zmiana od okresu do zapadalności.
Przykładowo T dla zmiany stopy procentowej o 0,01 % dla kontraktu wielkości 1000 000 - wynosi:
Wartość T (jednostki pieniężne)
1 rok
100
(tj. 1 000 000 x 0.0001x 12/12)
9 miesięcy
75
(tj 1000 000 x 00001 x 9/12)
6 miesięcy
50
(………………. x 6/12)
3 miesiące
25
1 miesiąc
8.3
Współczynnik odpowiedniości pieniężnej K jest stosunkiem dwu odpowiednich wartości T.
Przykład
W celu zabezpieczenia sześciomiesięcznego aktywa kasowego trzymiesięcznymi kontraktami terminowymi współczynnik K jest równy 2. (t.j. 50/25). Innymi słowy, 2 kontrakty terminowe są potrzebne na zabezpieczenie kontraktu kasowego bo ten, konkretny kontrakt reaguje dwukrotnie silniej dla danej stopy procentowej niż trzymiesięczny.
Dociekliwym polecamy próbę odpowiedzi dlaczego tak być może???? Zagadnienie występowania zostanie omówione w innym miejscu dokładniej. W tym miejscu polecamy wziąć pod uwagę duration instrumentów i ich kształt krzywej dochodowości.
Przyjmijmy, że doświadczalnie wyliczone równanie regresji dla CD i trzymiesięcznych futures na stopę procentową daje następujące parametry - współczynnik regresji alfa:
\(\alpha = 0.12\)
\(h = 0.95\)
Czyli chcąc zabezpieczyć przed zmiana wartości portfel o wartości nominalnej 10 000 000 BPF w CD przy pomocy kontraktów futures na trzymiesięczna stopę procentową potrzebne jest:
\(If = \frac{10 000 000}{500000} \times \frac{50}{25} \times 0.95 = 38\) kontraktów
Jak widać ilość kontraktów jest różna od prostej zależności nominalnych wartości kontraktów na obu rynkach.
Podsumowując powyższe rozważania można stwierdzić:
Wartość \(\boldsymbol{W}\) portfela to:
Gdzie: \(\boldsymbol{P_k}\) - wartość pozycji kasowej a \(\boldsymbol{P_f}\) wartość kontrakty futures. \(\boldsymbol{h}\) - współczynnik zabezpieczenia.
Optymalna wartość \(h\) to taka wartość gdy zabezpieczenie będzie idealne czyli zmiana wartości portfela nie ulegnie zmianie niezależnie czy wartość kasowego aktywa wzrośnie czy zmaleje.
Czyli
Stąd:
Czyli ilość kontraktów futures \(I_f\) potrzebna do zabezpieczenia pozycji na rynku kasowym jest równa:
W przypadku dyskutowanych przykładów powyżej zmiany ceny aktywa na rynku futures były takie same jak zmiany ceny aktywa na rynku kasowym. Niestety nie zawsze tak jest w praktyce. Dlatego współczynnik zabezpieczenia h może być reprezentowany przez współczynnik regresji ceny instrumentu kasowego od ceny instrumentu terminowego. Współczynnik ten jednak może lepiej określać powyższa zależność jeśli będzie traktowany jako zmienny w czasie niż jako niezmienny.
W wielu pracach wykazano, ze prawdziwy związek między danymi finansowymi jest lepiej uchwycony, jeśli stosuje się modele o zmiennych w czasie parametrach niż modele o parametrach stałych. Często, w praktyce, stosuje się podejście zwane filtrem Kalmana by oszacować zmienny w czasie współczynnik hedgingu. Takie podejście często jest statystycznie bardziej efektywne i ma lepsze własności przewidywania.
14.4.2. Hedging portfela obligacji¶
Zabezpieczanie przed ryzykiem stopy procentowej portfela obligacji.
Podobne jak w każdym poprzednim przykładzie celem zabezpieczenia jest wyrównanie ewentualnych strat na kontrakcie kasowym zyskiem z kontraktu futures.
Ryzykiem, którego obawiają się zarządzający portfelem instrumentów dłużnych jest ryzyko stopy procentowej. Jeśli zarządzający obawia się, że w wyniku wzrostu stopy procentowej wartość jego portfela obligacji spadnie to ma przed sobą kilka możliwości rozwiązania tego problemu. Może spieniężyć (sprzedać) cały portfel a po wzroście stóp odkupić jego zawartość (a będzie on tańszy). Jednak musimy pamiętać o kosztach transakcyjnych i o tym, ze może być niemożliwym odkupić wszystkie poprzednio posiadane obligacje. Może on również, kolejna tańsza możliwość, użyć kontraktu futures na obligacje. Na większości rynków futures taki kontrakt jest wyceniany na podstawie wyceny koszyka obligacji „cheapest -to- deliver” (CDT lub na YouTube).
Tak więc kluczowym jest kupienie właściwej ilości kontraktów do zabezpieczenia. Należy więc wyliczyć współczynnik zabezpieczenia (hedge ratio), która to wielkość będzie zależeć od zmienności cen instrumentów na rynku kasowym i rynku futures. Ilość kontraktów, które należy użyć wynika z wielkości współczynnika zabezpieczenia, który możemy oszacować jako:
Nie musimy określać zmienności cen instrumentów. Jak już wiemy jeśli instrument kasowy jest mniej zmienny niż terminowy instrument zabezpieczenia to większa ilość instrumentów zabezpieczających jest potrzebna. Albowiem nie zawsze możemy używać obligacji zachowujących się jak obligacje - „cheapest to deliver”.
Wśród metod dostępnych do wyliczenia współczynnika zabezpieczenia w powyższym przypadku najbardziej powszechnymi są metody „współczynnika konwersji” zwana także współczynnikiem ceny oraz metoda „zmodyfikowanej duration” (zwana również jako wycena punktów bazowych.)
Współczynnik konwersji dla każdego instrumentu dłużniego jest podawany na bieżąco przez giełdy futures dla każdego instrumentu notowanego na tej giełdzie.
Kontrakt futures dla obligacji pozwala sprzedającemu spełnić zobowiązania dostawy używając każdej innej obligacji, tak by spełniać standard każdego kontraktu. Cena każdej z dostępnych obligacji może zostać wyliczona przez zastosowanie współczynnika konwersji. Współczynnik konwersji bazuje na matematycznym wyliczeniu wartości aktualnej netto, co pozwala na porównanie różnych dostępnych obligacji (z różnymi terminami do zapadalności i kuponami) na wspólnej bazie nominalnego kuponu.
Niektórzy autorzy (np. David Black - Financial Market Analysis) używa wielkości współczynnika ceny, który jest odwrotnością współczynnika konwersji.
Niech będzie sytuacja, gdy zarządzający portfelem spodziewa się wpływu ok. 1,5 milion USD, które to pieniądze zamierza ulokować w obligacje „cheapest to delivery” - CDT. Załóżmy, dla uproszczenia, że cena obligacji CDT i kontraktu futures na nie porusza się równolegle w czasie. Związek pomiędzy zmianą ceny kontraktu terminowego i ceny obligacji CDT są dane równaniem:
Gdzie :
\(\Delta P_f\) - zmiana ceny kontraktu terminowego na obligacje
\(\Delta P_{CDT}\) - zmiana ceny obligacji CDT
\(PF_{CDT}\) - współczynnik ceny dla obligacji CDT
Niech współczynnik ceny (zgodnie z tabelą giełdową) wynosi 1.20833. Oraz niech są handlowane po 125 za nominał 100. Aby zabezpieczyć wartość portfela potrzebuje ilość kontraktów \(I_f\) wyliczonych zgodnie z:
Gdzie \(h\) to współczynnik zabezpieczenia równy \(h = PF_{CDT}\), oraz
przy czym \(P_{CTD}\) to cena obligacji CTD.
Czyli innymi słowy:
To niezłe zabezpieczenie.
Wykazano jak można użyć kontraktów terminowych na obligacje do zabezpieczenia obligacji.
Kolejne pytanie to pytanie co może zrobić zarządzający używający kontraktów terminowych by zabezpieczyć obligacje inna niż CTD? Oraz drugie pytanie Jak można zabezpieczyć przy pomocy kontraktów terminowych na obligacje portfel obligacji?
Można posłużyć się dwoma metodami przybliżonymi:
Metoda oparta na wspł. konwersji (ceny)
Metoda zabezpieczenia oparta na duration
Metoda 1.
Załóżmy podobną sytuację jak poprzednio: 1,5 miliona USD i zamierzamy użyć obligacji 5- letniej o współczynniku ceny 1,1111 handlowanej w dniu planowania zabezpieczenia po 124 za nominał 100.
Załóżmy, że jeśli nastąpi określona zmiana stopy procentowej to zmiana ceny obligacji CTD zmieni się o 1,2 a cena obligacji, którą zabezpieczamy zmieni się o 1.8.
Te informacje posłużą nam do wyprowadzenia zmodyfikowane równania zabezpieczenia.
Jak zwykle ilość kontraktów potrzebna do zabezpieczenia \(I_f\) wynosi:
gdzie:
\(h_z\) to współczynnik zmiany zabezpieczenia dla obligacji zabezpieczanej
równy
\(\Delta P_{CDT}\) - zmiana ceny obligacji CDT przy takiej samej zmianie stopy procentowej
\(\Delta P_H\) - zmiana ceny obligacji zabezpieczanej przy takiej samej zmianie stopy procentowej.
Czyli liczba kontraktów wynosi:
Przybliżenie tej metody polega na tym że zmiana stopy procentowej o 1% nie powoduje zmian cen obligacji dwa razy większych niż zmiana stopy o 0.5%. Jak pamiętamy z analizy obligacji ta zależność nie jest liniowa. Dlatego dokładniej jest używać metody opartej na duration. Definicja duration została wprowadzona z równania:
Gdzie
\(D\) - duration obligacji (średni czas do zapadalności)
\(P\) - cena obligacji
\(Y\) - dochodowość do zapadalności (yield to maturity)
Aby wyliczyć współczynnik zabezpieczenia w tej metodzie należy podzielić zmianę ceny obligacji zabezpieczanej przez zmianę ceny obligacji CDT.
\(h_D\) = współczynnik zabezpieczenia uwzględniający „duration”.
\(h_D = \Delta P_H/ \Delta P_{CDT}\)
wpisując formalnie równanie (4) do powyższego wzoru i zakładając równoległe przesunięcie krzywych dochodowości otrzymujemy
Gdzie indeksy \(H\) odnoszą się do obligacji zabezpieczanej a \(CDT\) do obligacji ”cheapest to delivery”.
Zakładając duration obligacji CTD jako 10 lat oraz duration obligacji zabezpieczanej jako 14 lat otrzymujemy dla danych z poprzednich przykładów:
czyli w sensie duration 1 obligacja zabezpieczana jest równa około 1.4 obligacji CDT.
Konsekwencją będzie wyliczenie ilości kontraktów potrzebnych do zabezpieczenia kwoty zainwestowanej w obligacje z poprzedniego przykładu (czyli o cenie 124 i współczynniku ceny 1.1111):
czyli ilość kontraktów wynosi:
W przypadku portfela obligacji metodą najłatwiejszą do konstruowania strategii zabezpieczającej zużywając kontraktów futures na obligacje wydaje się być metodą biorącą pod uwagę duration portfela. Z analizy zachowania się ceny obligacji wiemy, że zmiana jej dochodowości skutkiem zmiana stopy procentowej jest nieliniowa, tak więc przybliżenie liniowe jest niedokładne. Branie pod uwagę duration portfela jako średni (ważony wartością) czas do zapadalności wszystkich instrumentów obligacyjnych portfela wydaje się być dokładniejszą metodą.
Mając, więc, do zabezpieczenia portfel obligacji określamy jego duration a następnie określamy współczynnik zabezpieczenia analogicznie jak w poprzednim przypadku.
Dla portfela otrzymujemy równanie na współczynnik zabezpieczenia \(h_p\) w podobne, jak równanie w poprzednim przypadku, w postaci
Z tym, że:
\(D_p\) - to duration portfela
\(P_p\) - to średnia ważona kapitałem cena obligacji w portfelu.
Mając wyliczony współczynnik zabezpieczenia dla portfela o określonej wartości potrafimy, analogicznie jak w poprzednim przypadku wyliczyć ilość kontraktów potrzebnych do zabezpieczenia portfela obligacji:
14.5. Hedging przy pomocy opcji¶
Opcje wydaja się być bardziej elastycznymi narzędziami do zabezpieczania w porównaniu z kontraktami futures. Jak to wynika z samej ich natury można przy ich pomocy starać się zbudować taką strategię zabezpieczania, która pozwoli na ograniczenie strat w przypadku niekorzystnego ruchu cen, ale pozwoli na osiągniecie zysku w przypadku sprzyjających zmian na rynku. Opcje są bowiem, ze swej natury niesymetryczne. Kontrakt futures jako zabezpieczanie ustalał cenę na danym poziomie ale uniemożliwiał skorzystanie z zysków.
Generalnie kontrakty terminowe są stosowane kiedy ilości aktywów i czas zamknięcia pozycji jest znany z dużą pewnością. Kontrakt terminowy ustala cenę określonej ilości aktywa w danym czasie w przyszłości. Jeśli któryś z wymienionych parametrów nie jest znany raczej stosuje się opcje.
Z rozważań na temat opcji znane są profile zysków i strat dla poszczególnych opcji.
Patrząc na te profile nasuwa się strategia zabezpieczenia przy pomocy opcji.
Jeśli posiadamy akcje ABC i chcemy zabezpieczyć się przed spadkiem ich ceny, rozwiązaniem jest wykupienie opcji put na tę cenę. Jeśli wykreślimy profil zysków i strat takiej strategii to łatwo jest dostrzec, że wynik takiej transakcji (long akcji i long put) ma taki sam profil jak posiadanie (syntetycznej) opcji call.
Czyli są możliwe dwie strategie zabezpieczania dające ten sam efekt końcowy. Czy to, że efekt zabezpieczenia jest taki sam znaczy, że są sobie równoważne??? I którą strategię należy stosować?
Mając bowiem akcje spółki ABC możemy zabezpieczyć się przed spadkiem ich kursu w określonym czasie, kupując do portfela opcje put wygasającą w tym właśnie czasie. Alternatywna strategia to sprzedać akcje i kupić opcje call. Którą wybrać?
Wybrać należy tańszą strategię, biorąc pod uwagę, koszty opcji, ewentualną wypłatę dywidendy i stopę wolną od ryzyka. Kupując dziś opcje put i trzymając ją do czasu wygaśnięcia ponosimy koszty zakupu opcji + koszty pieniądza w czasie, ale zyskujemy dywidendę. W przypadku sprzedaży dzisiaj akcji ABC zyskujemy wartość tej kwoty w czasie (do wygaśnięcia opcji call ale ponosimy koszty opcji call dzisiaj + jej wartość w czasie. Oczywiście nie mamy dywidendy. Które z dwu przepływów finansowych jest mniejszy, tę strategie stosujemy. Należy jeszcze uwzględnić w obliczeniach koszty transakcji.
Informacja
Generalnie stosuje się następującą zasadę zabezpieczania stosując opcje:
Jeśli pozycja jest zagrożona stratą w przypadku spadających cen to kupujemy opcje put lub sprzedajemy call.
Jeśli pozycja jest zagrożona stratą w przypadku rosnących cen sprzedajemy opcje put lub kupujemy call.
Należy pamiętać jakie zobowiązania ciążą na sprzedającym opcje (konieczność dostarczeni/ kupienia aktywa podstawowego po ustalonej cenie) a jakie na kupującym opcje (ryzyko ograniczone do wysokości straty premii).
14.6. Strategie opcyjne polegające na stosowaniu kombinacji opcji¶
Do zabezpieczenia pozycji możemy użyć kombinacje opcji. Opcji, które dotyczą tego samego aktywa, tego samego czasu wygaśnięcia opcji i tej samej ceny wykonania (jeśli nie potrafimy przewidzieć kierunku ruchu cen). Przykładem takiego zabezpieczenia jest strategia, która polega na kupnie (bądź sprzedaży) zarówno opcji put i call (at the money) (w równych ilościach).
14.6.1. Dwie opcje¶
Strategia ta jest nazywana Straddle - stelaż.
Strategie ta jest stosowana, kiedy oczekujemy dużej zmienności ceny aktywa, ale nie wiemy, w którą stronę
Jeśli kupimy straddle zyskujemy jeśli akcje przesuną się dużo w dowolna stronę.
Maksymalna strata to cena kupionych opcji.
Należy ponownie podkreślić, że w przypadku używania opcji w celu zabezpieczenia możemy kupować opcje albo je wystawiać. Opcje nie są instrumentami o symetrycznym ryzyku. Wystawiając opcje ryzykujemy konieczność dostawy aktywa więc koszty nabycia takiego aktywa są często znacznie wyższe niż premia za opcje a w przypadku kupna opcji ryzykujemy tylko stratę w wysokości jej ceny.
Powyższy przykład to strategia Long stradle czyli nabywamy opcje i nasze ryzyko jest ograniczone do sumy premii zapłaconych za opcje a
ewentualny zysk jest praktycznie nieograniczony.
Jednakże, jeślispodziewamy się, że cena wykonania aktywa podstawowego nie zmieni się zastosujemy strategie short straddle czyli wystawimy tą samą ilość opcji kupna i sprzedaży na tą samą cenę wykonania i czas zapadalności. Jeśli sprzedamy straddle,zyskujemy jeśli akcja nie przesunie się w żadnym kierunku. Strategia jest opłacalna w sytuacji gdy spodziewana jest stabilizacja ceny instrumentu podstawowego na poziomie ceny wykonania S1. Wadą tej strategii może być brak ograniczenia maksymalnej straty jaką można ponieść w wyniku zastosowania strategii, gdy cena jenak ulegnie zmianie. Maksymalny zysk wynikający z zastosowania takiej strategii jest równy sumie premii uzyskanych z tytułu wystawienia opcji.
Inne strategie tego typu.
Generalnie można stosować strategie opcyjne polegające na kupieniu i sprzedaży opcji o różnych cenach wykonania S1 i S2 różnych od siebie (poszerzony zakres niepewności). Przypadek gdy S1=S2 już został omówiony powyżej.
Takie strategie zwane są vertical spread.
Można też używać kombinacji opcji o różnych okresach wygaśnięcia czyli tak zwany calendar spread. Pozwala to na zyski jeśli cena wyjdzie poza obszar miedzy cenami wykonania.
Oczywiście można stosować kombinacje opcji o różnej cenie wykonania S1 i S2 oraz o różnych terminach wygaśnięcia T1 i T2. (tzw Zeus hedge).
Wybór strategii zależy od tego przed czym chcemy się zabezpieczyć.
Bardziej dokładne omówienie stosowania kombinacji opcji i jego praktycznych ograniczeń, można znaleźć np. w pracy autorstwa Jerzego Dzieży - O możliwościach arbitrażu na Giełdzie Papierów Wartościowych w Warszawie 2005 napisanej dla GPW i dostępnego w sieci Internet i na stronach GPW. Oraz w pracy Krzysztofa Piontka pracownika Katedry Inwestycji Finansowych i Ubezpieczeń, Akademii Ekonomicznej we Wrocławiu a zatytułowanej Weryfikacja parytetu kupna/sprzedaży dla opcji notowanych na GPW w Warszawie - Problemy oraz przykłady strategii arbitrażowych - praca dostępna w sieci Internet.
14.6.2. Delta hedging¶
Wiedząc jak wrażliwa jest cena opcji na zmianę parametrów rynkowych wiedząc o znaczeniu współczynników greckich opcji (kolejne pochodne cząstkowe- Patrz opcje rozdział Analiza wrażliwości ) Możemy posłużyć się tą wiedzą konstruując strategie zabezpieczania pozycji (portfela) przed zmianami cen na rynku. Metoda zwana hedgingiem delta neutralnym ma na celu utworzenie i zachowanie pozycji portfela składającego się z pozycji kasowej i pozycji opcyjne mającego deltę równą zero (delta neutralna na zmiany)i zachowanie jej w czasie. Delta neutralny hedging jest taką strategią, w której stosunek pomiędzy ilością opcji i ilością akcji (aktywa zabezpieczanego) jest równa odwrotności delty opcji.
Zmiana ceny opcji przy zmianie ceny aktywa podstawowego nosi nazwę współczynnika delta. Jest to, innymi słowy, miara wpływu zmiany wartości instrumentu bazowego na kurs opcji. Odpowiada na pytanie; O ile zmieni się kurs opcji na wskutek zmiany wartości instrumentu bazowego?
Dla opcji call, korzystajac z modelu Blacka Scholesa
A dla opcji put:
Korzystając z prostego przekształcenia widać, ze:
Ponadto, delta wskazuje ilość akcji potrzebnych do otworzenia zwrotu z opcji.
Np., \(\Delta_{call} = 0.80\) znaczy ze działa jak 0.80 akcji. Jeśli cena akcji wzrośnie o 1, cena opcji call wzrośnie o 0.80. cecha ta pozwala na budowanie strategii zabezpieczających. Ale więcej o analizie wrażliwości można znaleźć w Analiza wrażliwości opcji.
Informacja
Budując strategie zabezpieczające bazujące na zachowaniu niezależności wartości od zmiany ceny (\(\Delta= 0\)) kierujemy się zasadą, która to zasada jest następująca:
Budując zabezpieczenie pozycji krótkiej/(długiej) w opcjach (europejskich) call polega na utrzymaniu pozycji długiej/(krótkiej) w N(d1) aktywach bazowych.
W przypadku opcji put, (opcje europejskie - delta ujemna) pozycje długą /(krótka) w opcjach put zabezpieczamy pozycja długą/(krótką) w [N(d1) - 1] akcjach bazowych.
Współczynnik delta zmienia się w wyniku upływu czasu do terminu wygaśnięcia opcji oraz zmiany wartości instrumentu bazowego. Przy zabezpieczaniu wystawionych opcji metodą delta hedging należy dokonywać okresowych korekt pozycji zabezpieczającej zgodnie ze zmianą współczynnika delta. Delta bowiem jest równa zero przez pewien czas i cierpi skutkiem zmian nie tylko czasu i zmienności ceny ale także wielkości mierzonych przez współczynniki theta i Vega (kappa).
14.6.3. Delta hedging, przykład na drzewie binarnym¶
Wyobraźmy sobie, że mamy rynek na którym opcja sprzedaży na aktywo ma cenę godziwą 15. Ponadto wyobrażmy sobie, że mamy chętnego na taką opcję za 16. Wynika z tego, że można zarobić 16-15=1 wystawiając opcję sprzedaży. Jednak wystawieniem opcji narażamy się na ryzyko poniesienia niczym nie ograniczonej straty! Czy możemy zarobić „naszą” złotówkę nie ponosząc ryzyka? Okazuje się, że tak i właśnie delta-hedging może nam w tym pomoć.
Postąpimy tak. Wystawimy za 16 opcje. Zgodnie z ideą hegdingu, będziemy utrzymywać taki portfel by w KAŻDYM scenariuszu ewolucji ceny aktywa, otrzymać zysk 1, wynikający z początkowej różnicy ceny godziwej i rynkowej.
Do ilustracji tej sytuacji wykorzystamy model binarny. Najpierw zbudujemy czteropokoleniowe drzewo cen aktywa, startując od wartości 100. Będzie to drzewo addytywne - zakładamy, że cena może wzrosnąc lub zmaleć o 20 w jednym kroku. Ponadto dla przejrzystości zakładamy zerową stopę procentową. Łatwo się przekonać, że w takiej sytuacji model będzie wolne od arbitrażu jeśli prawdopodobieństwa wzrostu lub spadku ceny aktywa będą równe \(\frac{1}{2}\).
Zacznijmy od zdefiniowania kilku pomocniczych funkcji:
Wygenerujmy więc nasze eksperymentalne drzewo cen aktywa i narysujmy je:
Wycenimy teraz opcję sprzedaży aktywa za cenę \(K\) w czasie \(t=3\). Zaczynamy od ceny opcji w czasie jej wykonania i propagujemy w dół drzewa obliczając za każdym razem średnie ważone z miarą arbitrażową \(p\). Dochodzimy w ten sposób do ceny opcji w czasie \(t=0\). Algorytm może być zaimplementowany na przykład tak:
Mając ceny opcji i aktywa w każdym miejscu drzewa, możemy wyliczyć współczynnik delta. W przypadku modelu dyskretnego będzie on dany przez:
czyli delta w danym węźle drzewa jest ilorazem różnic cen opcji i aktywa w chwili następnej. Wynika z tego, że deltę możemy policzyć dla wszystkich z wyjątkiem ostatniego pokolenia. Wykorzystując procedurę wizualizacyjną możemy obliczyć wszystkie delty dla naszego drzewa i zestawić wykres z wykresem ceny opcji.
Strategia delta hedge zakłada, że w każdym momencie powinniśmy mieć dokładnie tyle jednostek aktywa ile wynosi delta. Mamy więc:
Wystawiliśmy opcję za którą dostaliśmy 16
Tworzymy portfel składający się z aktywa i depozytu bankowego lub kredytu, na starcie mamy na depozycie 16 ze sprzedaży opcji
W każdym punkcie drzewa modyfikujemy portfel tak by mieć dokładnie \(\Delta\) jednostek aktywa. Jeśli trzeba to się zadłużamy.
Możemy więc łatwo zaimplementować funkcję calculate_evo,
która obliczy dla danego scenariusza w każdym momencie portfel
zabezpieczający. Następnie generujemy listę wszystkich scenariuszy i
w elementcie interaktywnym obliczamy kolejne portfele.
14.6.4. Strategia gamma - neutralnej (przy delta = 0)¶
Strategia polegająca na tworzeniu portfela o zerowym \(\Delta\) i zerowym \(\Gamma\) jednocześnie.
\(\Gamma\) drugą pochodną ceny opcji względem ceny akcji. \(\Gamma\) jest pierwsza pochodną \(\Delta\) w stosunku do ceny aktywa. \(\Gamma\) jest także nazywana krzywizną.
Jeśli gamma jest bliska zero, to znaczy \(\Delta\) nie zmienia się wiele ze zmiana ceny.
Więcej informacji na temat stosowania opcji do ograniczenia ryzyka można znaleźć w pozycji autorstwa Ryszarda Węgrzyna - „Opcje jako instrumenty ograniczenia ryzyka cen akcji. Problemy optymalizacji.” - Wydawnictwo Uniwersytetu Ekonomicznego w Krakowie - (2013).

